設計者に限りませんが、ベテランも最初は初心者です。言葉一つとっても知らないことばかりで当たり前です。なのに、学び始めた時に苦労するのは今も変わらないようです。
モノづくりでは、使用時に想定される使い方で壊れないように設計します。設計ポイントは応力集中以外にもあります。
ここでは、断面が長方形の梁を例に、断面係数と断面二次モーメントを使い、縦置きと横置きの梁の強さと断面形状を比較します。
長方形断面の梁の強さ
まずは、梁の強さと断面形状について説明します。
下図に示す長方形断面の梁があります。この梁の中央部分に重りを載せて(重力)を加えます。
ここで、問題です。
下図のように縦長に配置する場合と横置きに配置する場合とでは、どちらの梁の方が強い(より多くの荷重を加えられる)でしょうか?
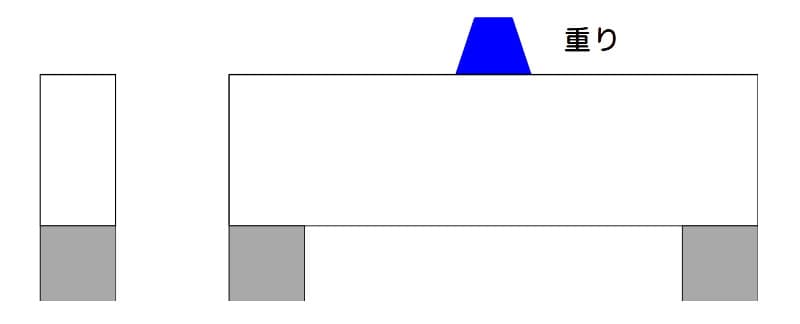
梁に重りを載せる:縦置き
図1 梁に重りを載せる:縦置き
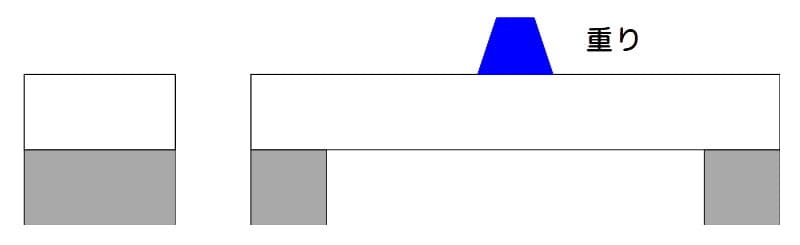
梁に重りを載せる:横置き
図2 梁に重りを載せる:横置き
理由は分からない、説明できないとしても、「直感的に縦置きの方が強い」と考えた方は正解です。

この答えに悩む方もいて、予想外のことを考えていて驚いたこともありますし、力学的なセンスがないのかな?と思うこともありました。
では、縦置きの方が強いことを、力学的に説明します。
強度計算では、断面二次モーメントと断面係数で判断することができます。
- 断面二次モーメントは変形のしにくさ(曲がりにくさ)、たわみを表します。
- 断面係数は、曲げ強さ、壊れるまでの強さ、壊れにくさを表します。

ここでは、断面二次モーメントと断面係数について、結果(数式)から説明します。詳細は別途まとめたいと思います。
断面二次モーメントで比べる
縦(\(h\))、横(\(b\))の下図に示す長方形の断面二次モーメント(\(I\))は、次式で表されます。
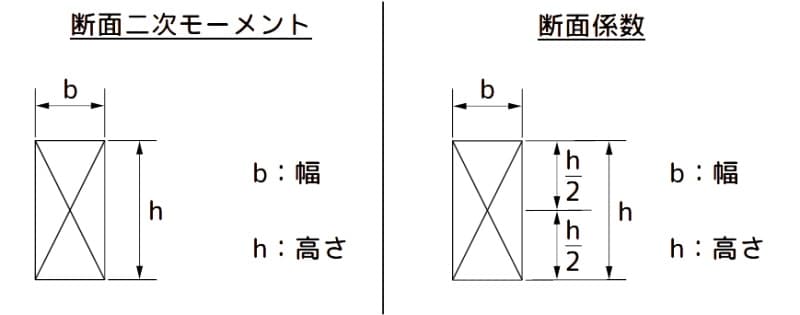
断面二次モーメントと断面係数の諸元
図3 断面二次モーメントと断面係数の諸元
$$I = \frac 1 {12} b h^3$$
上式において、から、縦(\(h\))は3乗になっていますので、横(\(b\))よりも縦(\(h\))を変化させた方が断面二次モーメント(\(I\))への影響が大きくなるということです。
ここで、縦置きと横置きを比較します。
縦置きの断面二次モーメント
縦(\(h\))、横(\(b\))を次の値とします。
$$h = 2$$
$$b = 1$$
断面二次モーメント(\(I\))は、
$$I = \frac 1 {12} b h^3 = \frac 2 3$$
横置きの断面二次モーメント
縦(\(h\))、横(\(b\))を次の値とします。
$$h = 1$$
$$b = 2$$
断面二次モーメント(\(I\))は、
$$I = \frac 1 {12} b h^3 = \frac 1 6$$
つまり、梁を縦に置くと、横に置いた場合よりも、断面二次モーメントの値は4倍となります。
断面係数で比べる
縦(\(h\))、横(\(b\))の図3に示す長方形の断面係数(\(Z\))は、次式で表されます。
$$Z = \frac 1 {6} b h^2$$
上式において、から、縦(\(h\))は2乗になっていますので、横(\(b\))よりも縦(\(h\))を変化させた方が断面二次モーメント(\(I\))への影響が大きくなるということです。
ここで、縦置きと横置きを比較します。
縦置きの断面係数
縦(\(h\))、横(\(b\))を次の値とします。
$$h = 2$$
$$b = 1$$
断面二次モーメント(\(I\))は、
$$I = \frac 1 {6} b h^2 = \frac 2 3$$
横置きの断面係数
縦(\(h\))、横(\(b\))を次の値とします。
$$h = 1$$
$$b = 2$$
断面二次モーメント(\(I\))は、
$$I = \frac 1 {6} b h^2 = \frac 1 3$$
つまり、梁を縦に置くと、横に置いた場合よりも、断面係数の値は2倍となります。
まとめ
モノづくりでは、使用時に想定される使い方で壊れないように設計します。設計ポイントは応力集中以外にもあります。
ここでは、断面が長方形の梁を例に、断面係数と断面二次モーメントを使い、縦置きと横置きの場合とで梁の強さを比較する方法について、以下の項目で説明しました。
- 長方形断面の梁の強さ
- 断面二次モーメントで比べる
- 縦置きの断面二次モーメント
- 横置きの断面二次モーメント
- 断面係数で比べる
- 縦置きの断面係数
- 横置きの断面係数

