実際の設計では複雑な形状や加工方法に加えコストも重要です。このため、基本的な断面形状の素材について、材料の強さやコストを比較し力学的な裏付けを知っていることが重要です。
梁の強さと断面形状との関係は、断面係数と断面二次モーメントで調べることができます。
ここでは、実際に使われている材料を例に、断面形状と断面二次モーメントを使って丸棒とパイプ、角材と角パイプの強さを比較します。
丸棒、パイプ、角材、角パイプの断面二次モーメントと断面係数
丸棒とパイプの断面二次モーメントと断面係数について説明します。
丸棒の断面二次モーメントと断面係数
下図に示す丸棒の断面二次モーメント(\(I\))と断面係数(\(Z\))は、次式で表されます。
$$I = \frac \pi {64} D^4$$
$$Z = \frac \pi {32} D^3$$
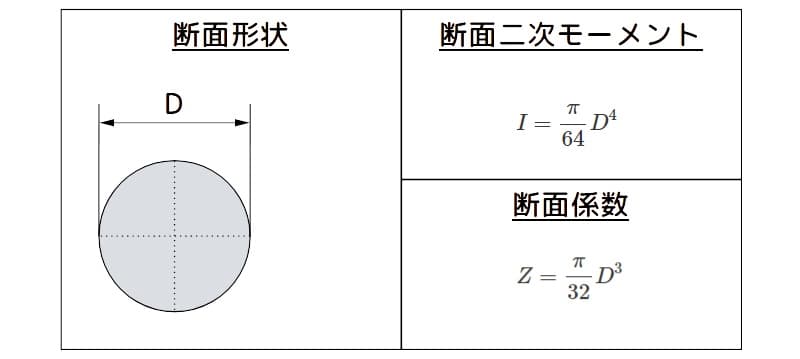
丸棒の断面二次モーメントと断面係数の諸元
図1 丸棒の断面二次モーメントと断面係数の諸元
パイプの断面二次モーメントと断面係数
下図に示す外径(\(D\))、内径(\(d\))のパイプの断面二次モーメント(\(I\))と断面係数(\(Z\))は、次式で表されます。
$$I = \frac \pi {64} ( D^4 – d^4 )$$
$$Z = \frac \pi {32 D} ( D^4 – d^4 )$$
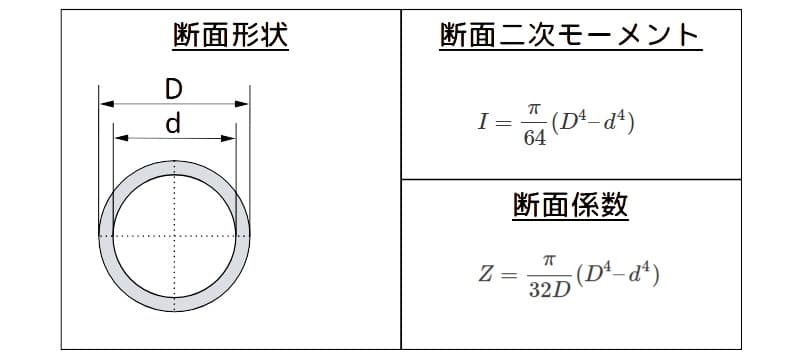
パイプの断面二次モーメントと断面係数の諸元
図2 パイプの断面二次モーメントと断面係数の諸元
角材の断面二次モーメントと断面係数
下図に示す縦(\(H\))、横(\(B\))の長方形の断面二次モーメント(\(I\))と断面係数(\(Z\))は、次式で表されます。
$$I = \frac 1 {12} B H^3$$
$$Z = \frac 1 {6} B H^2$$
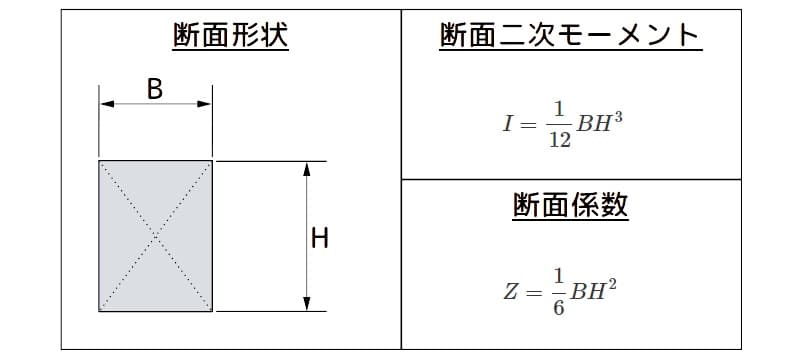
角材の断面二次モーメントと断面係数の諸元
図3 角材の断面二次モーメントと断面係数の諸元
なお、上式において、断面二次モーメントの縦(\(H\))は3乗になっていますので、横(\(B\))よりも縦(\(H\))を変化させた方が断面二次モーメント(\(I\))への影響が大きくなります。
角パイプの断面二次モーメントと断面係数
下図に示す外寸の縦(\(H\))、横(\(B\))、内寸の縦(\(h\))、横(\(b\))の角パイプの断面二次モーメント(\(I\))と断面係数(\(Z\))は、次式で表されます。
$$I = \frac 1 {12} ( B H^3 – b h^3 )$$
$$Z = \frac 1 {6 H} ( B H^3 – b h^3 )$$
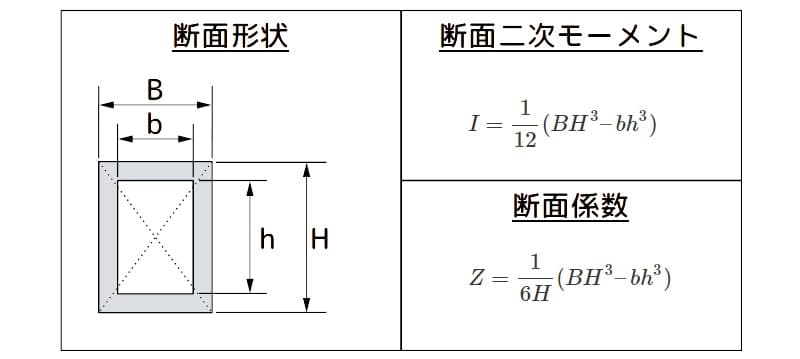
角パイプの断面二次モーメントと断面係数の諸元
図 角パイプの断面二次モーメントと断面係数の諸元
丸棒とパイプの比較
ここでは、断面係数で比較します。
丸棒の断面係数(\(Z_{rod}\))とパイプの断面係数(\(Z_{pipe}\))は、次式となります。
$$Z_{rod} = \frac \pi {32} D^3$$
$$Z_{pipe} = \frac \pi {32 D} ( D^4 – d^4 )$$
丸棒とパイプの形状(寸法)を以下の値とします。
- 丸棒:直径(\(D = 1\))
- パイプ:外径(\(D = 1\))、内径(\(d = 0.9\))
- パイプの厚さ(\(t\))を直径の5%としています。
上記値を入れて計算すると、
$$Z_{rod} = 0.0981$$
$$Z_{pipe} = 0.0337$$
$$Z_{rod} / Z_{pipe}= 2.91$$
となり、丸棒の断面係数はパイプの約3倍となります。
この時、丸棒とパイプの断面積をそれぞれ、\(S_{rod}\)、\(S_{pipe}\)とすると、
$$S_{rod} = D \ \pi = 0.785$$
$$S_{pipe} = D \ \pi \ – \ d \ \pi = 0.149$$
$$S_{rod} / S_{pipe}= 5.26$$
となり、パイプの断面積は丸棒の約1/5となります。つまり、材料が1/5で済むということになります。
以上の試算結果をまとめると、断面係数による単純な比較となりますが、上述の外径サイズの同じ丸棒とパイプを比較すると、パイプの方が強さ3倍弱、コストは1/5強という結果になります。
設計におけるQCDについては、以下の記事をご参照ください。
丸棒と角材の比較
角材と角パイプの比較は、丸棒とパイプと同様の結果が予想できますので、ここでは丸棒と角材とを断面係数で比較します。
丸棒の断面係数(\(Z_{rod}\))と角材の断面係数(\(Z_{square}\))は、次式となります。
$$Z_{rod} = \frac \pi {32} D^3$$
$$Z = \frac 1 {6} B H^2$$
丸棒と角材の形状(寸法)を以下の値とします。
- 丸棒:直径(\(D = 1\))
- 角材:縦(\(H = 1\))、横(\(B = 1\))
上記値を入れて計算すると、
$$Z_{rod} = 0.0981$$
$$Z_{square} = 0.1666$$
$$Z_{rod} / Z_{square}= 0.58$$
となり、丸棒の断面係数は角材の約60%となります。
この時、丸棒と角材の断面積をそれぞれ、\(S_{rod}\)、\(S_{square}\)とすると、
$$S_{rod} = D \ \pi = 0.785$$
$$S_{square} = B \ H = 1$$
$$S_{rod} / S_{square}= 0.79$$
となり、丸棒の断面積は角材の約80%となります。つまり、材料が約2割少なくて済むということになります。
以上の試算結果をまとめると、断面係数による単純な比較となりますが、上述の丸棒の直径と角材の縦横が同じ寸法の場合、丸棒の強さは角材の約60%、コストは約20%低いという結果になります。
参考:断面二次モーメントと断面係数の違い
断面二次モーメントと断面係数とはどの様なものなのかについて、同じような内容(意味)もありますが列挙しています。
断面二次モーメントは、次の様に変形のしにくさ(曲がりにくさ)を表します。
- 曲げモーメントに対して材料(梁など)がどの程度耐えられるかを判断するために使われる。
- 材料(梁など)のたわみにくさを表す。
断面係数は、次の様に、材料の曲げに対する強さを表します。
- 断面形状による曲がりにくさ(たわみにくさ)を表している。
- 曲げモーメントに対してどれだけ抵抗できるかを表している。
- 曲げ応力の生じにくさを表している。
- 曲げに対する抵抗力、強さを表している。

正直なところ断面二次モーメントと断面係数の違いを言葉で説明するのが難しいです。
断面二次モーメントと断面係数については、以下の記事もご参照ください。
まとめ
実際の設計では複雑な形状や加工方法に加えコストも重要です。このため、基本的な断面形状の素材について、材料の強さやコストを比較し力学的な裏付けを知っていることが重要です。
ここでは、実際に使われている材料を例に、断面形状と断面二次モーメントについて、以下の項目で説明しました。
- 丸棒、パイプ、角材、角パイプの断面二次モーメントと断面係数
- 丸棒の断面二次モーメントと断面係数
- パイプの断面二次モーメントと断面係数
- 角材の断面二次モーメントと断面係数
- 角パイプの断面二次モーメントと断面係数
- 丸棒とパイプの比較
- 丸棒と角材の比較
- 参考:断面二次モーメントと断面係数の違い



