ここでは、FFTアナライザによる振動や騒音の基本的な計測方法(FFTアナライザの使い方)についてまとめています。
ハンマリングについては、以下の記事をご参照ください。

1. 振動・騒音とFFTアナライザ
1.1 振動問題は音から見つかる
機械や家電製品などの騒音や振動問題は、まずは、「うるさい(騒音)」、「変な音がする(異音)」といった音の問題として始まることが多く、騒音や異音がどこから聞こえてくるか、どうして騒音や異音が発生するのかを調べていきます。
この際に使うのがFFTアナライザと呼ばれる計測器です。
1.2 振動や騒音と原因を探す
まずは、振動や騒音が発生している場所と、どのような振動や騒音が出ているかを調べます。例えば、どこから「問題の音が出ているのか」、「どの部品が振動しているのか」を探っていきます。
FFTアナライザを使い、振動であれば加速度センサーを使って振動の大きさを、騒音であれば音の周波数と強さを調べていきます。
実際には、「この部分(部品)を手で押さえると、問題の音が小さくなる」といった様に、振動や騒音の発生している場所や部品を見つけられることもあり、計測データにより詳細を調べていきます。
また、音は、ある部品の振動によって発生していることもあり、この場合には、音に関する指摘から始まるトラブルシュートも、最終的には振動対策につながっていきます。
1.3 振動の計測とFFTアナライザ
製品等の各部位(部品)から発生する振動が周波数の何Hzなのかは、製品あるいは部品の構造(形状)や材料により決まります。これを固有振動数(共振周波数)と呼びます。
FFTアナライザによる周波数分析データを利用すると、対象物のどこから音が出ていて、どの部位が何Hzで振動しているのかを調べることもできます。
後ほど紹介するバットの振動解析では、
- FFTアナライザを使い伝達関数(周波数応答関数)を計測する。
- 伝達関数の大きさと位相情報を利用してバットの共振周波数(固有振動数)における振動モード形を作成する。
- 振動モード形から、バットがどの様に振動するのかを考察する。
をします。
また、従来からの振動分析による設備管理・異常診断に加え、OA機器や家電製品など、静音性の評価や騒音原因及びその対策方法を検討するなど、振動や音の分析は様々な分野で行われています。
1.4 FFTアナライザを使う際のポイント
FFTアナライザを使う上でのポイントを紹介します。
- 対象物の振動を精度よく検出できる検出器(センサ)の選定
- FFTアナライザを正しく設定すること
- センサで検出した音や振動(センサの出力電圧)を正確にA/D(アナログ/デジタル)変換し必要な信号処理を行い、正確な振動計測データを得ること
機械の共振周波数の精密計測や周波数差の少ない騒音分析などもできるFFTアナライザですが、正確な計測のためにはノウハウがあります。
なお、正しい計測のためのノウハウは、今後も重要ではありますが、FFTアナライザの内部処理については、ブラックボックスとして扱ってもよいと考えています。
FFTアナライザの内部処理の一部を紹介します。
- サンプリング(標本化)とA/D変換
- サンプリング定理
- エリアシングを防ぐためのフィルタ(アンチエリアシングフィルタ)
- トリガ(ハンマリング試験では必須です。)
- 校正(キャリブレーション)
2. ハンマリング試験
ハンマリング試験の利点・欠点、ハンマリング時の注意点、計測したデータの確認方法などについて説明します。
2.1 ハンマリング試験とは
ハンマリング試験は、打撃試験とも呼ばれ、対象物をインパルスハンマで加振し、その結果生じる振動を加速度センサーなどで計測する試験方法です。
対象物の振動的な特性を調べたり、実験モード解析に使う伝達関数(周波数応答関数)の計測を行う場合などに、広く使われている試験方法の1つです。
インパルスハンマによるハンマリング試験は、準備が簡単で手軽に行えるため、簡単そうに思われがちですが、実際には意外に奥の深い試験方法でもあります。簡単な方法であるがゆえに、計測者の技術・経験やデータ処理(FFTアナライザの設定)が計測データに大きな影響を及ぼすからです。
実験モード解析は、共振周波数(固有振動数)と振動モード形(固有モード形状)を伝達関数(周波数応答関数)から求めます。したがって、計測する伝達関数の精度は、振動モードの形状に大きな影響を与えます。
プレテストやプレ解析のように、おおよその振動モード形状を把握するだけならまだしも、CAEと組み合わせて設計にフィードバックしたい場合には、精度のよい計測データや実験解析データを得ることが必須となってきます。
次項から、ハンマリング試験や実験モード解析に必要な基本的な知識について説明します。
2.2 ハンマリング試験の利点・欠点
ハンマリング試験の利点・欠点をまとめると次のようになります。
ハンマリングの利点
- 装置が簡単
- インパルスハンマ、センサ(加速度センサー)、FFTアナライザがあればよい。
- 方法が簡単
- 加振器では必須となる加振点の固定が不要。
- 応用範囲が広い
- 基本的にインパルスハンマで加振できるものなら計測できます。
- インパルスハンマは、大小様々なものが市販されています。
ハンマリングの欠点
- ガタや粘性などの非線形性を持つものには、基本的に適しません。
- 計測データの精度が、実験者の技術に大きく影響を受けます。
- 加振力の大きさ、周波数範囲などの調整がやりにくい(人に依存します)。
- 計測者が加振の調整をするには熟練の技術が必要ですし、人が調整する(加減する)と加振の再現性(繰り返し精度よく加振できるか)が問題となります。
- ハンマリングにより対象物に損傷を与える可能性があります。
2.3 インパルスハンマについて
一般的なインパルスハンマは、片手で軽くインパルス加振できる大きさですが、小型の対象物に対しては、全長10cm程度の小型のものから、大型機械や構造物などを加振できる大型のものまで様々な種類の製品が市販されています。
計測対象にあたる部分に使うインパクトチップは、対象物に合わせて各種材質のチップを使い分けます。
以下に、一般的なインパルスハンマのリンク先を紹介します。
インパクトハンマー PCB Piezotronics, Inc.
(当ブログでは、インパルスハンマと呼んでいます)
2.4 窓関数
ハンマリング試験(伝達関数の計測で使う)代表的な窓関数を下表に示します。
| 種類 | 周波数分解能 | 用途 |
|---|---|---|
| レクタンギュラ | 良 | インパルス波形などの過渡信号 |
| ハニング | 普通 | 一般的な連続信号 |
| フォース | - | インパルス波形などの過渡信号 |
| 指数 | - | 減衰信号 |
表1 代表的な窓関数
- レクタンギュラウィンドウは、方形窓または矩形窓とも呼ばれます。
2.5 ハンマリング試験の注意点(対象物の特性による影響)
対象物の非線形性
ハンマリング試験は、ガタなどの非線形を含む対象物には適しません。
ガタなどの非線形性を含む対象物を加振した場合、均一な加振や再現性のある計測が困難なためです。
対象物の減衰
対象物の減衰が大きい場合、応答がすぐに消えてしまい周波数分解能が低下してしまいます。
また、加振エネルギーが加振点周辺で吸収され、対象物全体を加振するのが難しくなります。
2.6 計測データの確認方法(よい計測データがとれたかどうかの確認)
ハンマリング試験は簡単に行えるので、良い計測結果も簡単に得られるように思われがちです。しかし、加振系に人が加わり実験者の技術の影響を受けてしまうため、良い結果を得ることは意外に難しいものです。
結果の有効性や計測精度を検証するための指標を以下に列挙します。
コヒーレンス関数(関連度関数)
コヒーレンス関数は、系の入力と出力の因果関係の度合を示すもので、0から1の間の値をとります。
- 1の場合は、その周波数における系の出力がすべて計測入力に起因していることを示しています。
- 0の場合、その周波数における系の出力は、計測入力にまったく関係ないということになります。
- 0~1の場合は、計測とは無関係な信号、系内部で発生しているノイズ、系の非直線性または系の時間遅延などがあると考えられます。
コヒーレンス関数が低下する原因には、以下のようなものがあります。
- 加振信号の中に検出できないノイズの混入
- 応答信号の中にノイズの混入(加振の再現性を向上させる)
- ハンマリングを平均化のために繰り返す中で、加振位置や方向がばらつくこと
- がたなどの非線形性の存在
応答信号のノイズ対策には、打撃の再現性を向上させて、平均化回数を増やすことで対応します。
加振信号のノイズは、同じ加振をしていないことになり、正しい平均化にならないため、フォースウィンドウを使用します。
反共振点近傍ではコヒーレンス関数が低下しますが、これは単に応答が小さく信号が誤差に埋もれているためなので、あまり気にする必要はありません。ただし、このような場合の反共振点近傍のデータは、モード特性を求めるためには使用しないほうが良いと考えています。
再現性(ハンマリング試験で同じように加振できたか?)
ハンマリング試験終了後、少なくとも1点は、試験時と同じ加振を繰り返し、結果を比較して再現性を確認します。
例えば、計測点が1~100点まである場合、計測点1から順に加振していき、計測点100まで計測が終わった後、もう1度計測点1で計測し最初の計測点1のデータと比較します。
比較した結果、加振中に対象物の構造などが変化していないか、一様に加振できたかどうかを判断し、違いが大きいと判断すれば最初からやり直しとなります。
線形性(加振力の振幅依存性)
加振力の大きさ(ハンマリングの強さ)で周波数応答関数が違ってくる場合、加振力の大きさを何通りか変えて周波数応答関数(伝達関数)を計測します。
周波数応答関数が異なる場合、対象物には振幅に依存する性質があると考えられます。(振幅依存性と呼ばれています。)
他の方法との比較
「結果がおかしい」、「何かおかしい」と経験的に感じる場合には、加振器を使うなど、他の方法と比較してみます。
大変抽象的ですが、直感が正しいことも実際には結構ありました。
3. ハンマリング試験での振動計測
振動計測(ハンマリング)の手順について、順に説明します。
3.1 実験モード解析に必要な計測データ
振動計測に限らず計測をする場合には、「何のために計測をするのか」という目的を明らかにすることが重要です。
振動計測の例を2つ紹介します。
例1 実験モード解析:対象物の振動モード形状を確認したい場合
- 計測データ:周波数応答関数(伝達関数)
- 計測方法:各計測点の伝達関数をできるだけ同一条件で計測
- FFTアナライザのチャンネル数:最低2チャンネル
例2 実稼動解析:対象物の実稼動状態での振動を可視化(実稼動アニメーション)したい場合
- 計測データ:パワースペクトル、クロススペクトル
- 計測方法 :多点の同時計測
- FFTアナライザのチャンネル数:計測点の数だけのチャンネル
上記は一例ですが、振動計測をする場合には、様々な目的がありそれに応じた計測データが必要になります。
だからといって、事例1や事例2のように計測の目的が定まっていれば、計測は単純作業なのかと言えば、そうでもありません。
例えば、解析周波数レンジ(測定する周波数の範囲)をどの程度に設定するかは、計測対象の固有振動数と何のためのモード解析か、ということに影響を受けます。いたずらに解析周波数レンジを高く設定すると、周波数分解能が不足し、低い周波数の振動モード形状を精度よく求めることが難しくなることもあります。
ここでの計測の目的は、「実験モード解析による振動の可視化」なので、FFTアナライザによる計測データとしては、伝達関数(周波数応答関数)が必要になります。
3.2 伝達関数(周波数応答関数)の計測に必要なデータ
実験モード解析に必要なデータは、伝達関数(周波数応答関数)があればよいのですが、正しく計測できたかどうかを確認するために、以下の計測データをFFTアナライザでモニタ(監視)します。
ここでは、伝達関数の計測時に観察する計測データ(FFTアナライザの関数)として、時間軸波形、パワースペクトラム、周波数応答関数、コヒーレンス関数について説明します。
FFTアナライザで入力信号と応答信号の2チャンネルを計測する場合を例にしています。
時間軸波形
センサ(インパルスハンマと加速度センサー)の信号レベルとFFTアナライザの電圧レンジが適正かどうか判断することができます。
伝達関数の計測では、インパルスハンマを使って同じ大きさ(FFTアナライザに入力される電圧のレベル)で加振できているかどうか(再現性)を確認します。
また、ハンマリングしている本人には気づかない様なダブルハンマに気付く(検出する)こともできます。
加速度センサーの信号は、インパルスハンマで加振した対象物の振動の大きさ(FFTアナライザに入力される電圧のレベル)と振動が減衰していく様子を確認します。
振動の減衰状況は、計測時間(FFTアナライザの取り込み時間)にも影響を与えるため、後に述べる窓関数の設定も必要になります。
パワースペクトラム
インパルスハンマのパワースペクトラムにより、設定した周波数レンジの中で何Hzぐらいまで加振できているかを確認します。
解析に必要な周波数までフラットに加振できていることが望ましく、必要に応じインパルスハンマのチップ変更などを行います。
高い周波数になるほど加振エネルギーが不足するため、ハンマリングによる加振が回数によらず均一に加振できているかがポイントになります。
対象物によっては、振幅依存性と呼ばれ、加振力によって応答が変わるものもあります。この場合でも同一条件で加振することにより、振幅依存性の影響を小さくすることができます。
応答点(加速度センサー)との関係では、加振点とセンサ取り付け位置が最も遠い位置関係にある場合においても、十分な加振力が得られる(応答点のパワースペクトラムの観測ができる)ことが重要になります。
本番の計測に入る前に、応答点を何箇所か選んで、一定の加振力で全ての応答点において必要なパワースペクトラムを観測できるか確認します。
特に計測ポイントが多い場合には、実際の計測点よりも少ないポイントのデータで振動モード形を確認したほうが、効率的な計測と実験モード解析による可視化につながります。
周波数応答関数
周波数応答関数は、(応答点)÷(入力点)のデータです。
周波数応答関数により、ある周波数における応答点の大きさと位相を知ることができます。
- 測定周波数の範囲で何Hz(ヘルツ)が大きい等
- 位相の向き(反転)
また、平均化処理をすることで、データ精度を高めるだけでなく、正しく計測できたかどうかを周波数領域で確認することができます。
ちなみにボード線図とは、周波数応答関数の位相特性とゲイン特性を1枚のグラフにまとめたものです。
コヒーレンス関数
平均化をした場合、1回目と2回目以降のデータの相関をみて、同じようにデータが取れたかどうかを確認することができます。
コヒーレンス関数は、その性質上平均化をしないと意味がなく、コヒーレンス関数を計測する場合は、必ず平均化を行います。
3.3 センサの選定及び設置
センサを計測対象物にどのような方法で固定するかにより、センサの周波数特性が変化します。
加速度ピックアップ
加速度ピックアップの選定と固定法についてまとめると、以下のようになります。
- 計測試料に対して十分に軽く、小さいものを選択する
- 加速度ピックアップを取り付けることにより、計測試料の固有振動に影響を与えます。
- センサケーブルの取りまわしなどにも注意する
- センサケーブルが対象物に接触して、減衰が変化する。
- インパルスハンマで加振したときに、ケーブルに接触してセンサの固定条件が変化し、計測データに影響が出ます。
センサの固定方法の一般的な長所・短所を下表に示します。
| 長所 | 短所 | |
|---|---|---|
| ワックス | 接着が簡単 |
接着度が弱い、熱に弱い。 高域の周波数まで検出不可能 |
| マグネット | 固定が簡単 | 接着度対象が限定される。 |
| 瞬間接着剤 |
固定が簡単 多種素材へ接着可能 |
計測試料を汚しやすい。 取り外す際に、センサを破壊しやすい |
| ネジ | 堅固な固定が可能 | 計測対象にピックアップ固定用のネジ穴を開ける必要がある。 |
表2 センサの固定方法の一般的な長所・短所
その他のセンサ
ハンマリング試験では、加速度ピックアップが使われることが多いのですが、私が使ったことのあるその他のセンサーについて紹介します。
渦電流式の変位計(変位センサ)
電磁力を利用したセンサで、対象物から離した状態(非接触)で高精度の変位測定が可能です。
その原理上、測定対象が金属である(渦電流が流れる)必要性があります。
レーザーを利用したセンサ
レーザーを利用したセンサには、レーザードップラー振動計や、レーザー変位計があります。
非接触でかつ高い周波数振動を計測することができます。
高精度、高感度のセンサーなので、測定ポイントのマーキングやセンサーを確実に固定する必要があります。
1軸の測定だけでなく、3軸同時の測定が可能なセンサーや、スキャニング方式のセンサーもありますが、高価なだけでなく、設置にも注意が必要です。
【参考】ハンマリングによる多点計測のポイント
正確な振動モード形を得るためには、マーキングした計測点を確実にハンマリングすることが重要です。
さらに、ハンマリングによる多点計測では、
- 実験モード解析であれば、目的の振動モード形を表現できる計測点であること
- 計測点を間違えずに計測すること
- 各計測点を正確かつ一様にハンマリングすること
がポイントになってきます。
計測点のマーキングはきっちりと
多点計測では、計測点のマーキングが重要なポイントになります。
金属バットのハンマリングの様に、計測点が直線的かつ数点~10点程度であれば、ハンマリング時に計測点とハンマリングの場所が多少ずれても計測データに大きな差とはならないことが多いと思います。
しかし、計測対称が平面や立体である場合、計測点数が数十点になってくるようになると、事前に計測点のマーキング(ハンマリングする場所と計測点番号)をきっちりとしておくことが、結果的に計測・解析時間の短縮につながります。
振動モード形を表せる計測点を選ぶ
計測点は、実験モード解析での振動モード形表示の形状モデルの座標点となるため、観測したい振動モード形をイメージして選定します。
が、まずは少ない計測点、計測回数でハンマリングを行い、どのような振動モード形をしているかのイメージをつかみます。
次に、詳しく観察したい部分の計測点を増やして、ハンマリングを行います。
FEMの固有値解析の利用
FEMの固有値解析による振動モード形状を利用して、計測点を決めていくこともできます。
この際、FEMの振動モード形状そのものを正確にハンマリング試験の計測点で表すのではなく、観察したい振動モード形状を表すことができる計測点を選ぶことがポイントになります。
レーザースキャニング装置による多点計測
多点計測では、ハンマリング以外に、レーザースキャニング装置を使う方法もあります。
解析モデルと計測点の対応についてはハンマリングと同様ですが、計測点数については、計測時間がハンマリングに比べ圧倒的に短いためそれほど気にする必要はありません。
というとメリットばかりのようですが、レーザースキャニング装置を使う場合、加振装置も併用することになるため、計測も大掛かりになりがちですし、何よりも費用対効果がネックになるかとが多いかと思います。
3.4 インパルスハンマによる加振方法
インパルスハンマによる加振方法
実験モード解析に使う伝達関数(周波数応答関数)を計測するため、インパルスハンマを使った加振試験について説明します。
対象物をインパルスハンマで加振し、その結果生じる振動を加速度センサーで計測します。
インパルスハンマによる計測手順は、加振点移動法と応答点移動法の2つの方法があります。以下、下図を使って説明します。
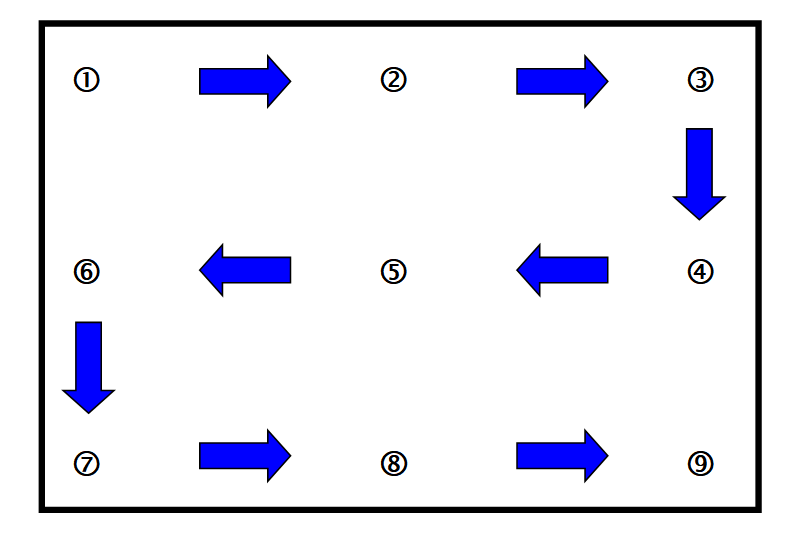
加振点移動法と応答点移動法の説明図
図1 加振点移動法と応答点移動法の説明図
加振点移動法
計測点の1箇所にセンサーを固定し、他の計測点を順次加振(ハンマリング)します。
加振点(ハンマリングする計測点)を移動していく方法です。
例えば、図において点①にセンサを取り付け、インパルスハンマで、点①から②、③、・・・、⑨と、順次ハンマリングを行います。
応答点移動法
加振点を計測点の1箇所に固定し、センサーを他の計測点に順次移動させます。
加振点(ハンマリングする計測点)を固定、つまり同じ計測点をハンマリングし、センサを移動させていく方法です。
例えば、図において加振点を点①に定め、センサ設置点を点①から②、③、・・・、⑨と、順次ハンマリングを行います。
インパルスハンマの選定・調整(サイズ、チップ)
インパルスハンマによる衝撃力(加振エネルギー)は、幅広い周波数範囲にわたり、ほぼ一定の力からなるため、その周波数範囲にあるすべての共振を起こすと考えられます。
衝撃力の振幅と周波数範囲(波形)はハンマのサイズ、長さ、材料および衝撃時の速度によって決まります。一般に加振できる周波数範囲は、衝撃キャップ(チップ)の材料によって決まり、加振エネルギーの大きさはハンマの質量と衝撃時(加振時)の速度によって決まります。
実験モード解析における加振力の周波数帯域の調整手順とポイントについて説明します。
- ハンマで試験対象を叩き(ハンマリングし)、FFTアナライザで平均化処理を行います。
- ノイズの影響を減らすため、必ず数回の平均化処理を行います。
- 計測結果を見て、以下の項目について確認します。
- 信号が適切であったか(SN比が十分かどうか)。
- 飽和現象(FFTの入力オーバーレンジや、ピークが一定時間平らになる)がないか。
- 計測中に、ときどきチップなどの接続部をチェックします。接続部が緩むと、センサーの信号が不安定になったり、ノイズが増加することがあります。
- 加振周波数帯域を確認します。
- インパルス波形の周波数波形(パワースペクトラム)が、対象物の共振周波数をカバーしているか。
- 必要に応じチップを変更します。
- チップは衝撃力をセンサーに伝えるとともに、センサー面を保護します。
- 剛性の異なるチップを使用することにより加振力を調整することができます。
- より高い周波数の応答が必要な場合、より硬いチップを使用します。
- 低い周波数の応答をより良くするには、より柔らかいチップを使用します。
- 必要に応じインパルスハンマのサイズを変更します。
- ハンマリングによる加振エネルギーを大きくするには、衝撃の速度かハンマの質量を大きくします。
【参考】チップによるインパルスハンマの感度調整
インパルスハンマによる加振力の周波数は、ハンマ先端のチップの材質によりおおまかな調整することができます。主なインパルスハンマのチップと特長を列挙します。
- ハード・チップ(金属製)
- インパルスの立ち上がり方が急峻で、高い周波数まで加振することができます。
- ダブルハンマリング(二度叩き)しやすくなり、パワースペクトル密度は小さくなります。
- ミディアム・チップ(プラスチック製)
- 金属製チップとビニール製チップの間の特性を持ちます。
- ソフト・チップ(ビニール製)
- パワースペクトル密度が大きく、加振エネルギーは低周波数域に集中します。
- 数Hz以下の加振を行うことは困難です。
インパルスハンマの使い方
ハンマリング試験は、計測実施者がインパルスハンマで対象物を加振します。つまり、加振系に人が含まれているため、加振器を使う場合に比べると人の技量や経験が加振の良否に大きく影響を与えます。
以下にハンマリング時のポイントを列挙します。
加振時
- ハンマはやわらかく軽く支える(握らない)。
- 人の力で叩くのではなく、ハンマの質量を利用して加振することが重要です。
- 叩き方は、できるだけ一様に一定にし、力の調節はハンマ側(大きさ、チップ等)で行います。
- 手はハンマに初速度を与えるだけとする(手で力を加えると加振が乱れ同じような加振ができません)。
加振点及び方向
- チップの先端は面積があるので、チップ中心を加振点に一致させるようにする。
- 加振点の位置決めを事前にきちんとしておく(加振点のマーキング)。
- 加振方向は、ハンマの力センサの向きと一致させます。
- ハンマが、対象物表面の法線方向から10度以上傾かないようにします(計測点に対しハンマを垂直に当てるイメージです)。
- 手を含めた加振系で回転運動とならないようにします。
加振の瞬間
- 加振の瞬間、ハンマが浮いた状態にあること。手で拘束しない(握らない)。
- インパルスハンマが対象物を叩くのと同時にすばやく引くイメージです。
- 当てるよりも引く方に意識を集中します。
【参考】加振エネルギーを叩き方で調整する場合
- 人が力の大きさを変えると、熟練者でも再現性を保つのが難しいので極力避けます。
- 単に衝突速度を変えるだけとし、叩く手の力を変えないようにします。
2度叩き(ダブルハンマリング)
2度叩き(ダブルハンマリング)とは、1度目の加振で振動を始めた対象物が、最初の反動で戻ってきたときにハンマと再度衝突してしまう現象のことです。
初心者では2度叩きとなってしまうことがよく見受けられます。これは、ハンマを手で拘束してしまうことに原因があることが多いです。

新人研修でバットのハンマリングをさせたところ、どうしても平均化できない人がいて、一発勝負のデータを採用したいこともありました。
計測者の練度が十分でない場合には、結局何度叩いても平均化ができない状態になってしまいます。このため、計測の効率を上げるためには、2度叩きをしないハンマリングの技術を習得することが必須となります。
3.5 計測対象物の支持方法
対象物の支持の重要性
振動計測をするためには、対象になる物(部品、機械や構造物などの小さいものから大きなものまで)を何らかの方法で固定する必要があります。
対象物の固定(支持)方法は、計測結果に大きな影響を与えるため、目的に合わせ対象物をきちんと固定(支持)する必要があります。インパルスハンマを使って計測対象を加振する場合、対象物の支持状態により結果が異なることがあるからです。
例えば、バットの伝達関数の計測では、グリップエンド部分を吊るして自由支持とする場合と、グリップエンド部分を固定した場合とでは、得られる振動モード形状が異なってきます。
加振ごとに支持条件が変化してしまうような場合には、計測データの精度や解析結果にも影響を与えてしまいます。
このため、振動計測においては、計測条件(FFTアナライザの設定条件など)だけでなく、どのような状態で加振したのかも含め記録として残しておくことにより、再計測(再実験)や解析の際に役立ちます。(質問する際には当然説明することになるので、記録を残すことは重要です。)
今ならばデジタルカメラを利用するなどして、対象物を含む全体の写真、加振方法、支持部(固定部)の写真などを残しておくことも簡単にできますので、面倒がらずに記録を残すことがポイントです。
対象物の固定条件は、自由、固定、弾性支持の3つに分けることができます。以下、それぞれについて説明します。
自由支持
自由支持とは、理想的には空間に浮かんだ状態で対象物が自由に動ける状態のことです。CAE(FEM)では簡単に設定できますが、実験では重力の影響で実現することができません。
しかし、実用的なレベルでは、比較的簡単にCAEなどの境界条件自由の状態を再現することができます。
例えば、対象物を吊ったり、空気バネを使ったり、ウレタンのようなスポンジ状の物の上に載せたりする方法により、自由支持とすることがあり、実際に使われています。
このときの注意点を以下に列挙します。
- 対象物を支持する物は、できるだけやわらかいものを選ぶこと
- 対象物に対して付加される質量や減衰の影響をできるだけ小さくすること
- 計測が安定してできるように対象物を支持すること
- 吊った場所やウレタン(スポンジ)などとの接触点が、固定のような特性を示す影響があるので、計測データ及び振動モード形状を見る際には、この点を考慮すること
自由支持の例を下図に示します。左側の図がウレタン上に置いた場合、右側の図が、対象物を吊ったイメージ図です。
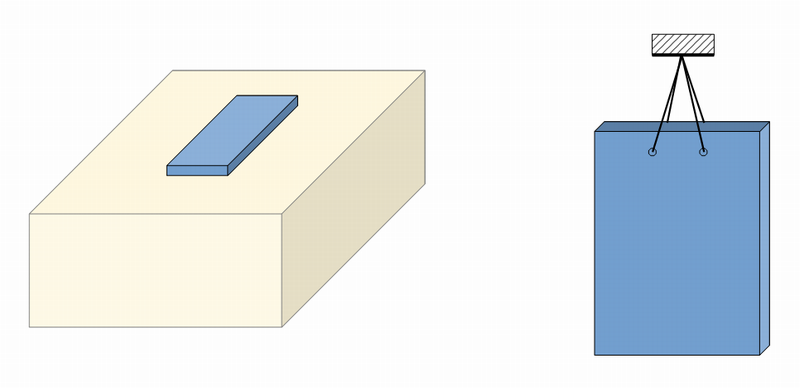
自由支持の例
図2 自由支持の例
固定支持
CAE(FEM)では、対象物の固定点の自由度をゼロに設定するだけで、固定支持を簡単に実現できますが、実験での実現は難しいため自由支持ほど一般的ではありません。
実計測で固定支持を実現するためには、質量と剛性が非常に大きい(理論的には無限大)物体に、対象物が一体になるよう溶接して取り付ける必要があります。
しかし、この方法は現実的には無理であるため、基礎や定盤のような物体にボルト締めをした状態を固定支持とみなしたりします。
この際の注意点を以下に列挙します。
- 基礎の一部または全体が、対象物と一緒に振動し付加質量としての挙動を示す場合があること
- ボルト固定をした場合、見掛け上は剛性が高そうでも、振動的には剛性の不足や接触面の粗さなどの影響による局部的な支持になっている場合があります。
- 実験モード解析をすると完全固定になっていないことを確認できます。
- 接触面では締め付けと直角方向の剛性が低下します。
- 基礎の弾性振動の影響により、主に高周波で連成振動が発生する場合があります。
このように、固定支持は自由支持よりも実現が困難であるため、振動計測ではできるだけ固定支持を避け、自由支持をする方が望ましいと言えます。
例えば、吊るしの状態を自由支持と近似することはできても、大きい基礎に対象物を設置したから固定支持になるとは限りません。
また、自由支持の結果から固定支持の結果を導くことは、自由支持の振動試験の結果から自由度を減らすことなので実現可能と言えますが、固定支持の結果から自由度を増やすことは現実的にはできないという側面もあります。
弾性支持
弾性支持は、対象物に対しバネなどを介して固定する方法です。
設置方法が難しい(構造的に複雑になる)ため、積極的に弾性支持を再現することは少ないようです。
ただし、実際の対象物が、構造上弾性支持のような固定方法になっている場合があります。
この様な場合の実験モード解析は、バネにより対象物が拘束されるため、自由振動だけでなく強制振動の要素も含まれることに注意が必要となります。
3.6 振動モード形と計測点の選定
計測点の選定は経験と観察力が重要です。

確かディスクブレーキのブレーキ鳴きを調べる時に、発生条件が分からないのに、観察していて、「ここから音が出ているので、この付近の振動モードが支配的なのではないか。」とある程度固有振動数まで絞り込んだベテランの方がいました。
振動モード形とは
ここでは、1本の棒を例に振動モード形について説明します。
物にはその物の構造や材料などにより決定される固有の共振周波数というものがあり、これを固有振動数呼びます。
固有モードは、周波数の低い方から1次、2次、・・・、N次モードと呼ばれ、振動試験で計測する信号には、1次~N次の振動モード、つまり固有振動数が含まれています。
これをイメージにすると下図のようになります。下図は、対象物には、1次モード、2次モード、・・・、N次モードが含まれているというイメージ図です。
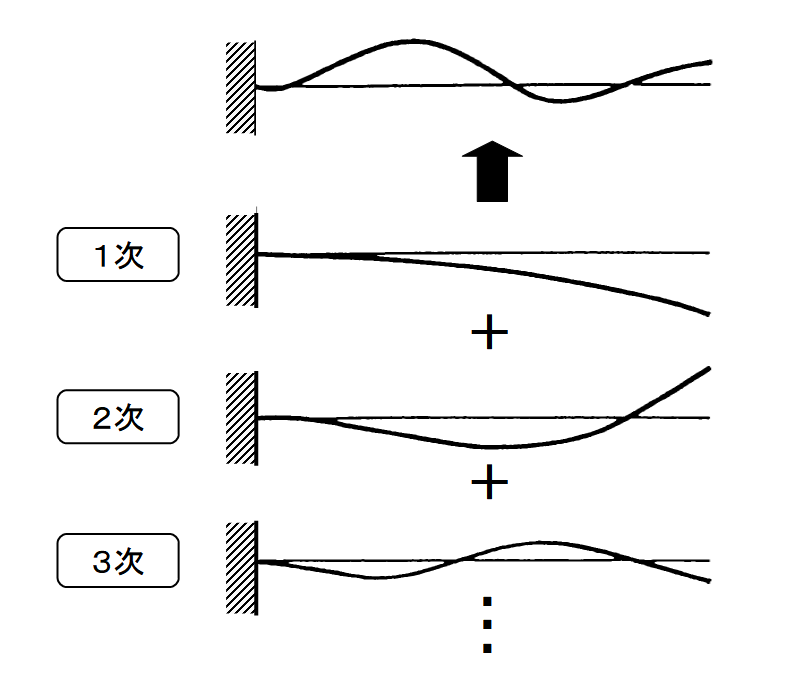
図3 振動モードのイメージ
線(棒)のモード形状(対象が梁状のもの)
実験モード解析においては、観察したい振動モード形を表現できるだけの計測点数が必要となります。
下図は1本の棒の両端の支持(固定)方法と振動モード形を並べています。各種支持方法(両端自由、片端固定、両端固定)により、振動モード形が違うことに注意してください。
対象物の形状が単純な棒でなくても、基本的な振動モード形状は共通になため、計測データや実験モード解析の結果を検証に役立ちます。
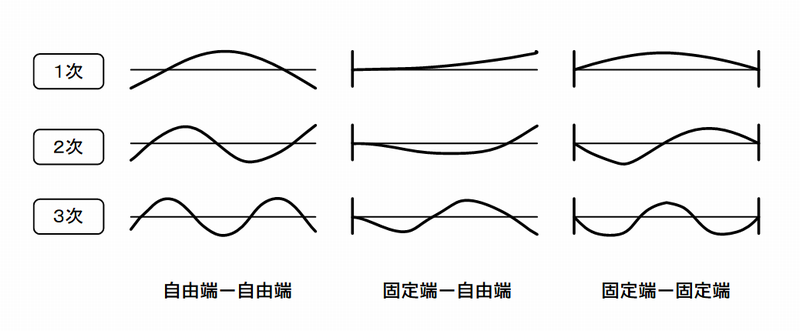
図4 各種支持方法と振動モード形
計測点数は、最低でも振動モード形状を表現できるだけの点数が必要となります。支持方法と最低必要な計測点の関係を、下図に示します。青の丸印と直線が、最小の計測点で表現できる各支持方法(固定条件)による振動モード形を表しています。
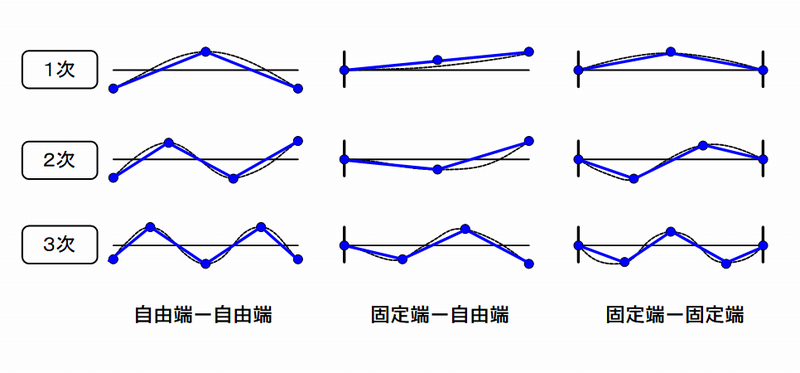
図5 振動モード形と計測点
また、実計測では完全固定は難しいため、固定端も計測点として含めています。
振動モード形状と最小計測点数の関係を下表に示します。
| 次数 | 両端自由 | 片端固定 | 両端固定 |
|---|---|---|---|
| 1 | 3 | 2(固定端含む) | 3(固定端含む) |
| 2 | 4 | 3(固定端含む) | 4(固定端含む) |
| 3 | 5 | 4(固定端含む) | 5(固定端含む) |
| N | N+2 | N+1 | N+2 |
表3 振動モード形状と最小計測点数の関係
面のモード形状(対象が平面の場合)
平面のモード形状は、棒(梁)のモード形状を平面に拡張する、つまり、X・Y方向の振動モード形を組み合わせで平面の振動モード形状を考えます。
平面の振動モード形の例を下図に示します。この図では、X方向の振動モード形が1次で、Y方向の振動モード形が3次の場合には、1-3モードと呼んでいます。
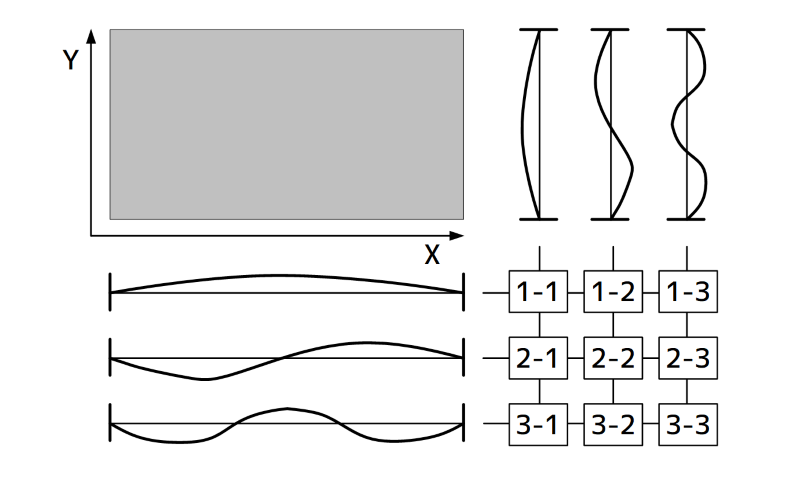
図6 平板の振動モード形と計測点の関係
機械のフレームなど平板のような単純な形状でない場合には、例えば10Hzの振動モードであれば、10Hzの振動モードと呼ぶことが一般的かと思います。
計測点数の考え方
基本的には、以下の考え方を組み合わせて、計測点数を決めることになります。
計測点数
計測点は多いほどきれいな振動モード形状を得ることができますが、計測時間だけでなく計測の難易度(同じように加振する)も高くなるため、全体の振動モード形状の傾向をつかんでから、計測点数を決める方が結果的には効率よく計測及び解析を進めることができます。
振動モードの個数
多数の振動モード形状を確認したい場合には、伝達関数を計測する周波数範囲を広く(共振周波数の数を多く)設定し、計測点数を減らして対象物がどのような振動をしているのか(振動モード形状を持つのか)を全体的に把握した後、より詳しく観察したい周波数範囲の計測点を増やし詳細な解析をします。
対象周波数が分かっている場合
問題となる(解析したい)周波数が分かっている場合には、その周波数の前後の共振周波数を観察するため、その付近の共振周波数が低い方から何個目かで、計測点をどの程度細かくするかを決めることができます。
振動モード系の節と加振点(可制御・可観測)
対象物をハンマリングする際、振動モード形の節を加振した場合には、その振動モード形の共振周波数(固有振動数)は計測できないことに注意が必要です。
同様に、振動モード系の節にセンサを設置した場合には、その振動モード形の共振周波数(固有振動数)は計測(観測)できないことに注意が必要です。
【参考】基本的な振動モード形
平板を例に、平板の支持方法(拘束条件)による振動モード形状の違いを、FreeCADの固有値解析を使った振動モード形をまとめました。
以下をご参照ください。
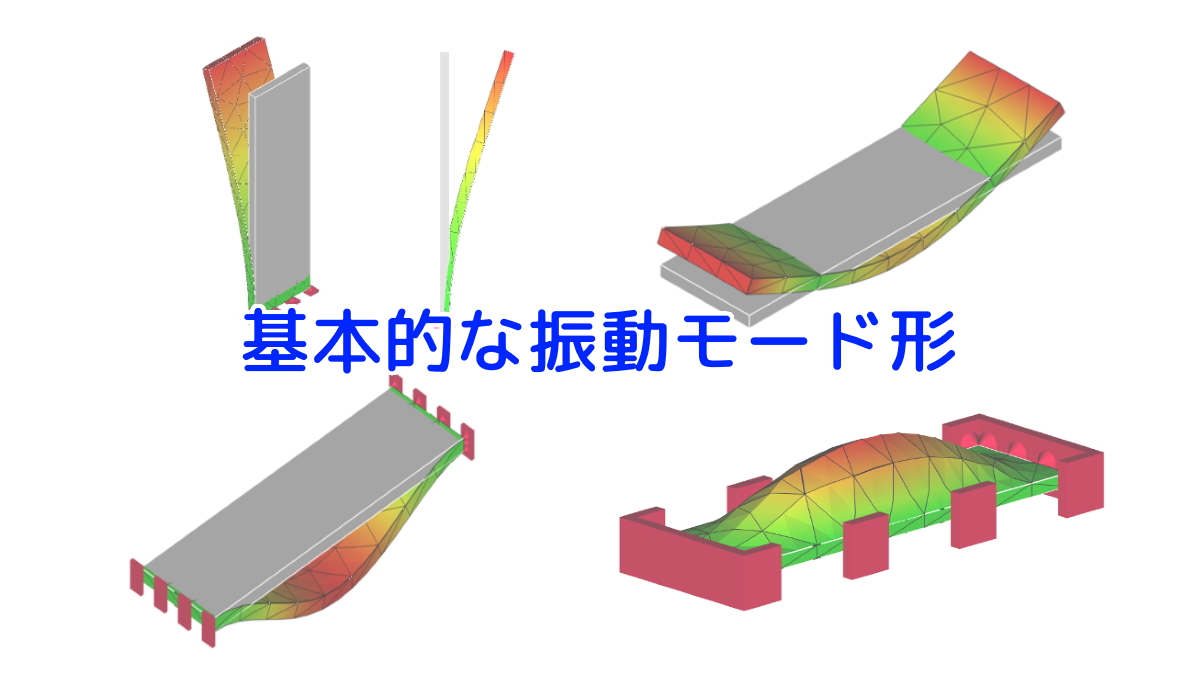
まとめ
ここでは、ハンマリング試験や実験モード解析でのFFTアナライザによる振動の基本的な計測方法(FFTアナライザの使い方)についてまとめました。
- 振動・騒音とFFTアナライザ
- 振動問題とFFTアナライザについて説明しました。
- ハンマリング試験
- ハンマリング試験の利点・欠点や注意点、必要な計測データについて説明しました。
- ハンマリング試験での振動計測
- ハンマリング試験で確認する計測データ、インパルスハンマの使い方、計測対象物の支持方法、計測点の選定などについて説明しました。


