ここでは、ホームランを振動から考えてみる方法の1つとして、振動モード形状に着目したバットの振動解析のうち、以下について説明します。
- 計測:ハンマリング試験による周波数応答関数(伝達関数)の計測
- データ処理:簡易的な振動モード形状の作成
ここでは、ハンマリング試験により得た伝達関数から、簡易的に振動モード形状を作成する方法について説明します。
なお、金属バットのハンマリング試験について体験実習ガイドを想定してまとめていますので、併せてご参照ください。

ハンマリングによる伝達関数(周波数応答関数)の計測方法
計測対象のバットは減衰が小さいため、ハンマリングによる応答が収束する前に、次のハンマリングをしてしまう可能性があります。
このため、計測が終了した後、バットに手を触れ、残留振動とバットの揺れを抑えてから次のハンマリングを行います。
計測点を下図に示します。計測点は5か所、センサは計測点①に設置します。
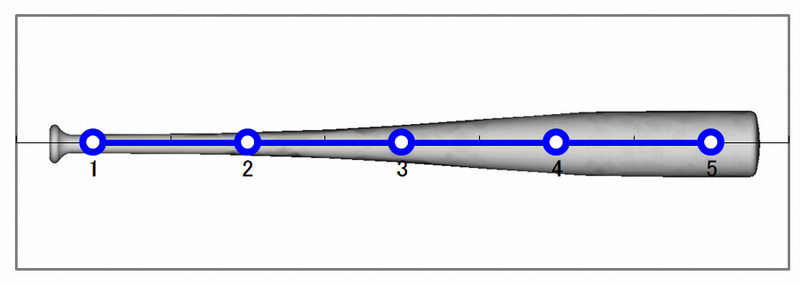
バットの計測点
下図は、周波数応答のゲイン(アクセレランス)、位相の計測データの一例です。
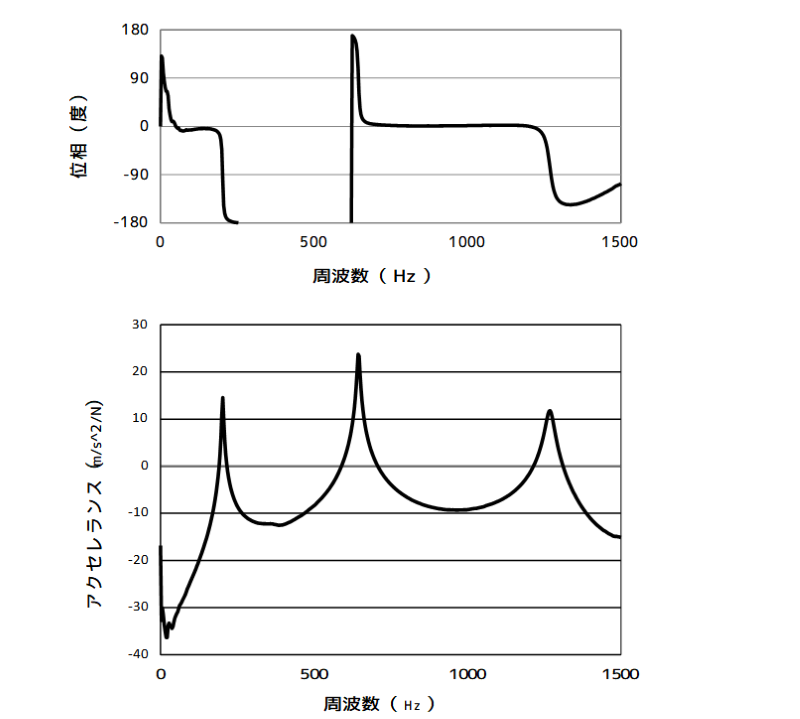
周波数応答関数のデータ例
簡易的な振動モード形状の作成
ゲイン(振動の大きさ)及び位相(振動の向き)データ整理
計測した周波数応答関数から、以下の表を作成します。
バットの1次から3次モードの共振周波数における周波数応答関数の大きさ(ゲイン)の値と位相(プラスかマイナスか)を記入します。
| 計測点 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1次モード | 43 | 33 | 39 | 25 | 35 |
| 位相 | + | - | - | - | + |
| 2次モード | 35 | 44 | 34 | 34 | 34 |
| 位相 | + | - | + | + | - |
| 3次モード | 11 | 9 | 15 | 15 | 13 |
| 位相 | - | - | + | - | + |
表 計測結果の一例
振動モード形の作成
表計算ソフトを使ったバットの振動モード形の作図例を以下に示します。
上からバットの1次、2次、3次モードです。
計測点を増やすとより滑らかな振動モード形を得ることができます。
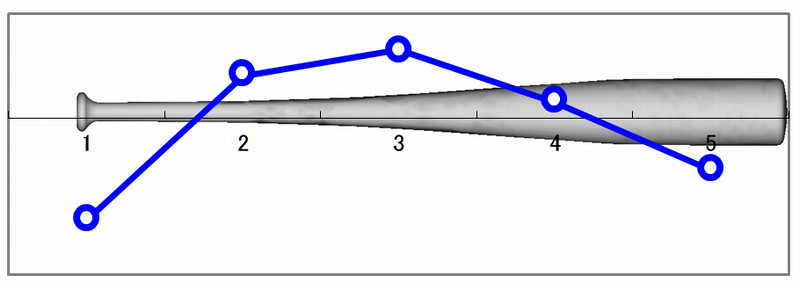
バットの1次モード
(1)バットの1次モード
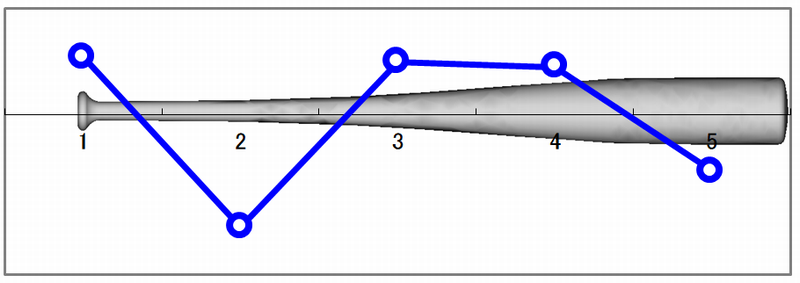
バットの2次モード
(2)バットの2次モード
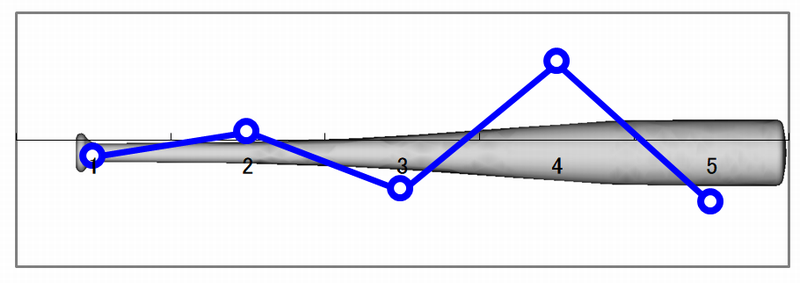
バットの3次モード
(3)バットの3次モード
図 表計算ソフトを使った作図例
【参考】ハンマリングによる多点計測
ここでの例では計測点を5点にしていますが、2次、3次の振動モード形について考察するためには、計測点を増やすことが必要になります。
例えば、バットの例であれば、5か所の計測点の間に4点追加して合計9点とするとより滑らかな振動モード形を得ることができます。
また、計測点を増やすことで平板等の面についても、ここで紹介した周波数応答関数による簡易的な振動モード形の作成は可能です。
平面の振動モード形の可視化であれば、表計算ソフトを利用して振動モード形を表示することもできますので、工夫してみてください。
まとめ
ここでは、ハンマリング試験により得た伝達関数から、簡易的に振動モード形状を作成する方法と作成例について以下の項目で説明しました。
- 計測:ハンマリング試験による周波数応答関数(伝達関数)の計測
- データ処理:簡易的な振動モード形状の作成


