ここでは、実験モード解析と理論モード解析(FEMによる固有値解析)のうち、振動モード形状に着目したバットの振動解析について、以下の項目を説明します。
- 実験モード解析
- CAEによるモード解析(FEMによる固有値解析)
- 実験モード解析の分類
専門用語や理論的な内容なので、軽く目を通していただけるとよいかと思います。
実験モード解析
ここでいう実験モード解析は、モード特性(固有モード、固有振動数、モード減衰比)を実験的に同定することを意味しています。
モデルという観点からは、モード特性(固有モード、固有振動数、モード減衰比)はモードモデルを、物理特性(質量、剛性、減衰)からは物理モデルを作成することができます。
3つのモード特性のうち、固有振動数、モード減衰比は、対象の系全体で共通であり、加振点や応答点が変わっても変化しないため、全体項と呼ばれます。
固有モードは、対象物の系の内部の応答の分布状態を示しており、加振点や応答点による変化するため、局所項と呼ばれます。

理論モード解析(FEMによる固有値解析)
CAE(FEM:有限要素法)でのモード解析(固有値解析)(このブログでは、実験モード解析と区別するため理論モード解析と呼んでいます)では、運動方程式から固有値解析によりモードモデルを作成し、振動モード形を表示、あるいはアニメーションとして可視化します。
これに対し、実験モード解析では、対象物の周波数応答関数(伝達関数)から、カーブフィットによりモード特性を求め、振動モード形を表示あるいはアニメーションとして可視化します。

FEMの固有値解析と実験モード解析の違い
有限要素解析(FEM)による理論モード解析(固有値解析)と実験モード解析、両者共最終的に振動モード形を得ることができる点は確かに同じですが、振動モード形を得る方法(プロセス)が異なる点には注意が必要です。
下図に、実験モード解析とFEMによる固有値解析の違いを示します。
- 実験モード解析は、実物のバットから解析モデル(モード形)を作ります。
- FEMによる固有値解析は、バットの形状データから解析モデルを作ります。
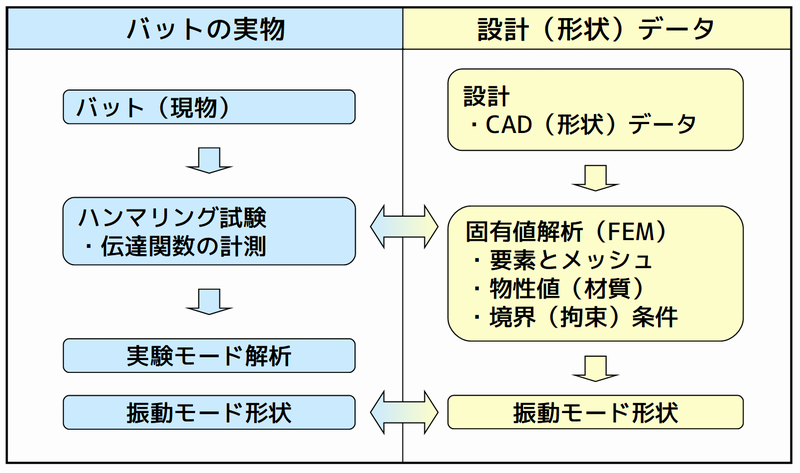
振動モード形を作成する方法の比較
実験モード解析の自由度による分類
ここで、実験モード解析の方法を自由度で分類すると、1自由度法と多自由度法に分けられます。
1自由度法は、対象物に含まれる複数のピーク(共振周波数)を、互いに独立な1自由度系のピークであるとの前提で、各固有モードと特性を求める方法のことです。
多自由度法は、異なる固有モード間の影響を考慮しながら、複数の固有モードのモード特性を同時に決定する方法のことです。
多自由度法は、さらに1点毎の多自由度法と多点同時参照の多自由度法に分類され、両者ともさらに周波数領域法と時間領域法とに分類できます。
1点参照は、加振点移動法もしくは応答点移動法のように、加振点または応答点(センサ)を1つに固定しデータを計測し、1点参照のカーブフィット処理を行います。
多点参照では、多点の加振点または応答点(センサ)を使用するため、計測が大規模になる傾向があります。しかし、対象物がほぼ同じモードを持つ場合にも、多点参照カーブフィットは、1点参照よりも精度良くモードパラメータを求めることができます。
このように、実験モード解析には、1自由度法のように簡単なものから、多点参照多自由度法などのように複雑な解析を行う方法もありますが、簡単だからよくないということはなく、計測データの精度や解析結果に求める内容などに応じて、選択することになります。
以下に、1自由度法と多自由度法の概要を説明します。
1自由度法
実験モード解析の対象となる機械や構造物は、多自由度系(連続体)です。多自由度系の周波数応答関数(伝達関数)は、1自由度系の周波数応答関数の重ね合わせで表現することができます。
対象物の固有モードの共振周波数付近で、減衰が小さい(ピークが鋭い)場合には、この共振周波数近傍の周波数応答関数を1自由度系であると仮定して、この固有モードだけのモード特性を個別(独立)に求めることができ、これを1自由度法と呼びます。
なお、以下のような場合には、1自由度法では精度が落ちるため、多自由度法が適しています。
- 減衰が大きくピークがなだらかな場合
- 隣接するピークが接近している場合
- ピークが小さい場合
- 他の大きなピークの裾に含まれてしまいピークとして識別が難しい場合
- ノイズが大きい場合
多自由度法
多自由度系の周波数応答関数は、複数の1自由度系の周波数応答関数の和として表すことができます。
仮に、対象となる系が非線形性を含まず、さらに、計測した周波数応答関数の計測値に全く誤差を含まないのであれば、理論式による周波数応答関数と計測データの周波数応答関数は一致するはずです。
しかし、実際の振動計測では、対象となる系に多少なりとも非線形性が含まれていることが多く、加振、計測、信号処理など、様々な原因による誤差が混入することもあり、計測データと理論式が一致しないことが一般的です。
対象となる系で周波数応答関数を計測した段階では、対象物のモード特性は、依然未知であるため、理論値の周波数応答関数も求められていません。
そこで、計測データに誤差が含まれていることを仮定し、計測データに「全体として最も適合するように」最適な理論曲線を選択します。実際には、理論式のモード特性を決めることになり、複数の固有モードのモード特性を同時に決めてしまうのが、多自由度法です。
「全体として最も適合するように」という表現は分かりにくいかもしれませんが、よく使われる方法は最小自乗法です。
まとめ
ここでは、実験モード解析と理論モード解析(FEMによる固有値解析)のうち、振動モード形状に着目したバットの振動解析について、以下の項目を説明しました。
- 実験モード解析
- 理論モード解析(FEMによる固有値解析)
- FEMの固有値解析と実験モード解析の違い
- 実験モード解析の自由度による分類


