FEM(有限要素法)解析で解析する際には、特異点に注意する必要があります。
特異点というと難しそうですが、CADで描く図面上の形状と実際のモノの違いや応力シミュレーションをする際のモノの固定方法(拘束条件)、外力(荷重条件)の設定の際の注意点と考えています。
市販されているFEMソフトであればソフト側で対応していることが多いと思われます。ここでは、FreeCADを使ってFEM(応力解析)で注意する特異点について説明します。
特異点が解析結果に与える影響
特異点とは、FEMのメッシュの違い(細かさの違い)により解析結果に違いが出てくる点のことです。
応力解析の場合に注意すべき特異点には、解析対象の形状で角(済)の部分、拘束条件設定部分の他、集中荷重を点でかけた場合などが相当します。
FEMの解析モデルは、外形こそ3Dとなっていますが、実際のモデルは多くの要素で構成されており、各要素は節点で相互につながっています。
下図は、ソリッドモデルでよく使うテトラ要素です。
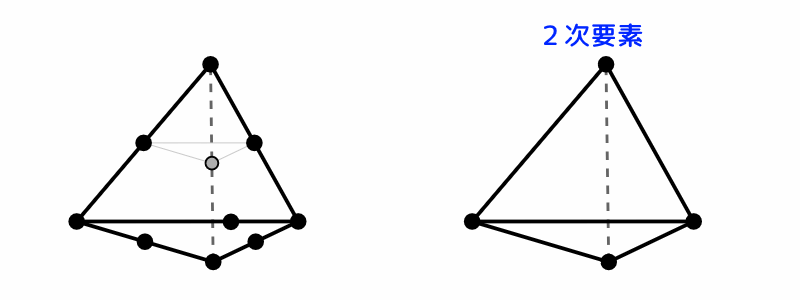
FreeCADのシェル要素 三角錐(テトラ)
図1 FreeCADのシェル要素 三角錐(テトラ)
また、FEMの解析座標系の自由度は、下図に示す、X、Y、Z軸の並進の3自由度に加え、各軸周りの回転3自由度の計6自由度になりますので、特に実験と解析値を比較する場合には拘束条件の設定に注意が必要です。

6自由度の完全拘束とするのではなく、並進の1軸のみ拘束するといったことです。感覚的には理解できるのですが、説明できるほどに理解できていませんので、ご了承ください。

解析座標系
図2 解析座標系
以下、特異点の例について説明します。
有限要素法の要素については、以下をご参照ください。

角部分の特異点
角部分の特異点とは、例えば下図のL字金具の内側の直角部分のことです。
下図の右側がL字金具の変形が絶対変位、色が応力(フォン・ミーゼス応力)で赤い部分に応力が集中しています。
下図左側は内側の角部分にRを追加したもので、最大応力はL字金具両端の角部分に発生しています。
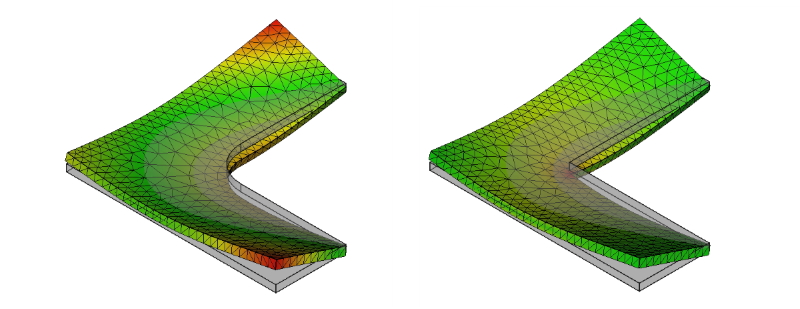
L字金具の応力解析例
図3 L字金具の応力解析例
3D CADで解析モデルと作る場合には、上図のL字金具の内側の角の部分は90度になります。しかし、実際のL字金具は、製作過程でRの大小の差はあってもRがついています。

実際に直角に加工する必要がある場合には、放電加工という特殊な方法を使います。
上図のL字金具の内側の角部分が特異点と呼ばれます。上記形状の他、切り欠きでも同様なので、特異点近傍の解析値を知りたい場合には注意が必要です。
拘束条件による特異点
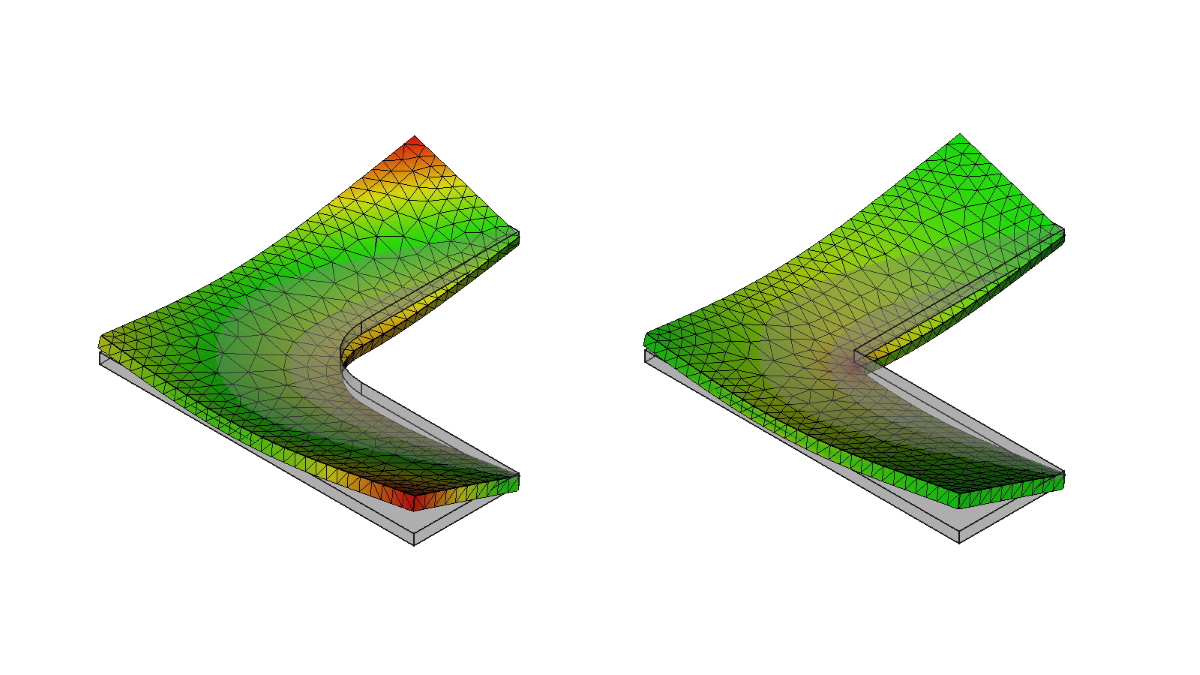
下図は、片持ち梁の応力解析結果の例です。
片持ち梁の左側の面を拘束し、先端部の上方向に力を加えています。
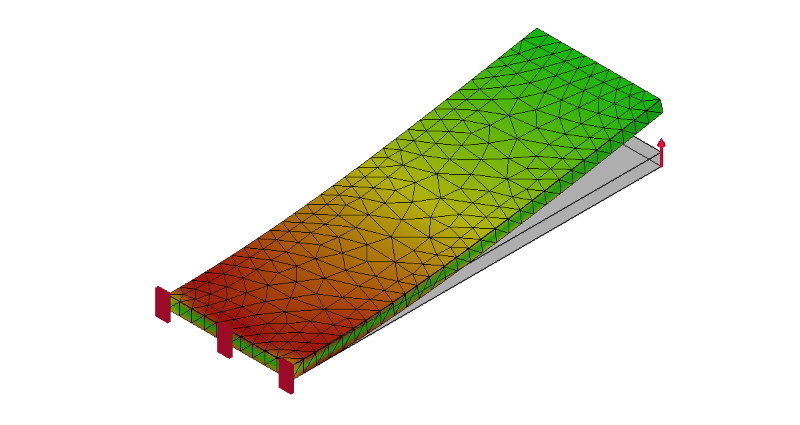
片持ち梁の応力解析例
図4 片持ち梁の応力解析例
この場合、特異点は、物体を固定している拘束部分となります。
下図は、上図を側面から見たものですが、拘束点に近い部分が赤色で応力が集中しているところが特異点になります。
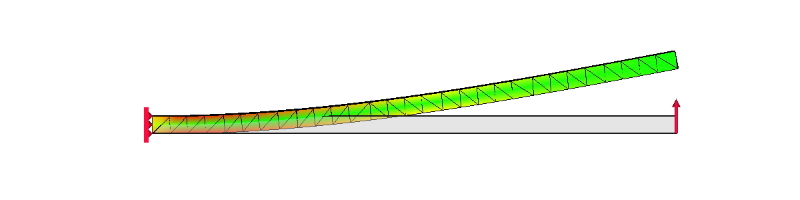
片持ち梁の応力解析例(側面図)
図5 片持ち梁の応力解析例(側面図)
拘束部分では、固定部分の変位が完全にゼロとなり伸縮しません。つまり、拘束部分が特異点となってしまい、現象としてはメッシュを細かくすると応力も変わってしまいます(真値に収束しないという意味です)。また、拘束を節点、ライン(線)や面で拘束すると解析結果に違いが出てきます。
実際の片持ち梁で先端に荷重を加えれば、拘束部分は変形しますし、ハンマリング試験で固定部分を加振しようとしても、片持ち梁の拘束部分をハンマリングすることは難しいのが現実です。
したがって、FEMで実際の応力値を求めたい場合には、拘束条件の設定にノウハウが必要となってくるため注意が必要です。
集中荷重による特異点
下図は、片持ち梁のメッシュですが、要素の1点に集中荷重を加えると、その点の応力は無限大になってしまい特異点となります。
つまり、応力は荷重と面積で表されますが、点には面積がゼロであるため、応力が無限大となってしまい特異点となります。
荷重を加えた点の応力を知りたい場合には、上述した拘束点と同様に、荷重についても集中荷重ではなく、分布荷重に変更する必要があります。

実際のモノにどの様に荷重がかかるかを想像すればよいということなのですが、実験を全く知らないとイメージがわきにくいかと思います。
設計者も体験でよいから実験や加工を経験した方がよいと私が考える理由の1つです。
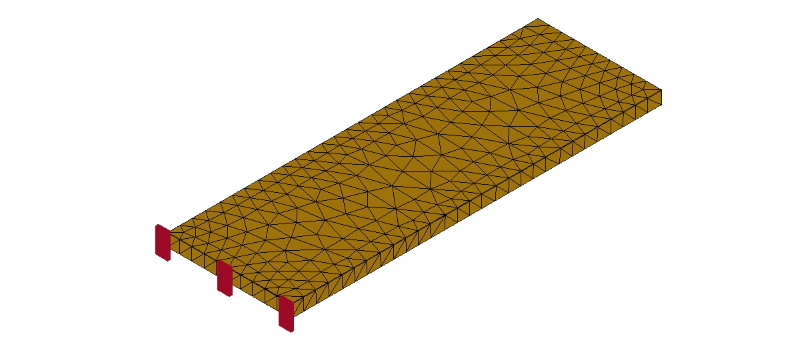
片持ち梁のメッシュ
図6 片持ち梁のメッシュ
なお、FreeCADのバージョン0.18では点(ノード)に荷重を加えることもできるようになった様なのですが、使い方が悪いのか私は実現できていないため、解析例がありません。
まとめ
FEMの特異点というと難しそうに聞こえますが、簡単にまとめてしまうと拘束や荷重を設定するときには、解析座標系の6自由度に注意することが必要です。
ここでは、FEMの応力解析では、解析モデルの形状、拘束や荷重条件について、以下の項目で説明しました。
- 特異点が解析結果に与える影響
- 角部分の特異点
- 拘束条件による特異点
- 集中荷重による特異点