ここでは、FEM(有限要素法)により得られた解析結果を評価するために必要な、FEM(有限要素法)の基礎知識として、
- 有限要素法と要素分割(メッシュ)
- メッシュの種類
- メッシュと計算精度
- メッシュの細かさについての考察
について説明します。
要素の選定や要素分割については、パソコンの性能向上とFEMのソフトウェアの進歩により、要素分割(メッシュ切り)において困る、手間がかかることも少なくなっていると思われます。
しかし、要素分割したモデルが解析目的に適したモデルになっているかを判断するために、有限要素法や要素についての基礎的な知識は不可欠だと考えています。
有限要素法と要素分割(メッシュ切り)
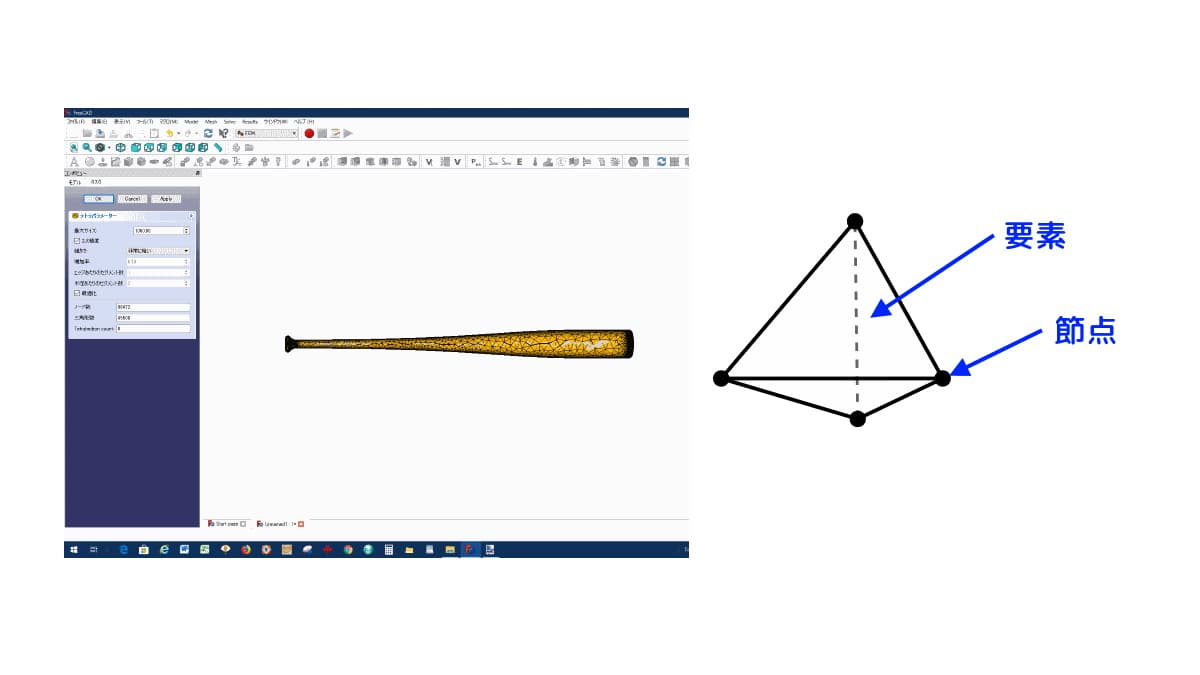
有限要素法という言葉から難しいイメージを持ちがちですが、「有限要素法」とは、構造物を複数の有限個の要素(メッシュ)に分割してシミュレーションを行うことです。
つまり、有限要素法では 「解析できるように解析対象の形状を要素で分割する」 ことが必要です。
バットの形状を要素で分割した例を下図に示します。
下図は、メッシュ分割を「非常に粗い」、「中程度」、「非常に細かい」場合のメッシュの分割例です。
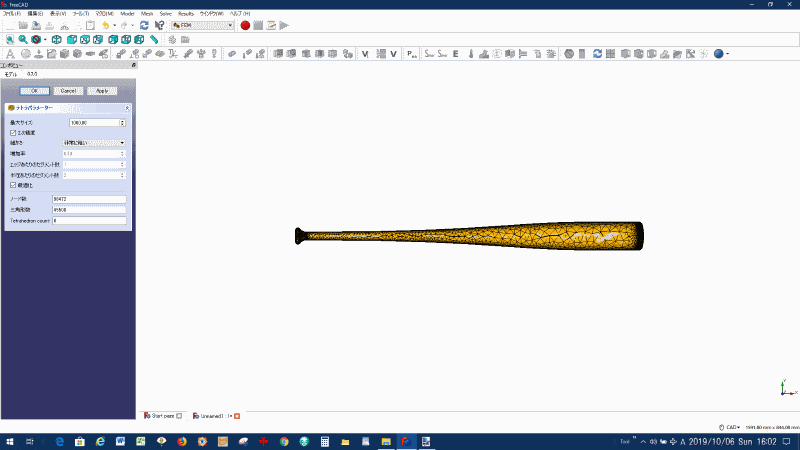
バットのメッシュ分割:非常に粗い
図1 バットのメッシュ分割:非常に粗い
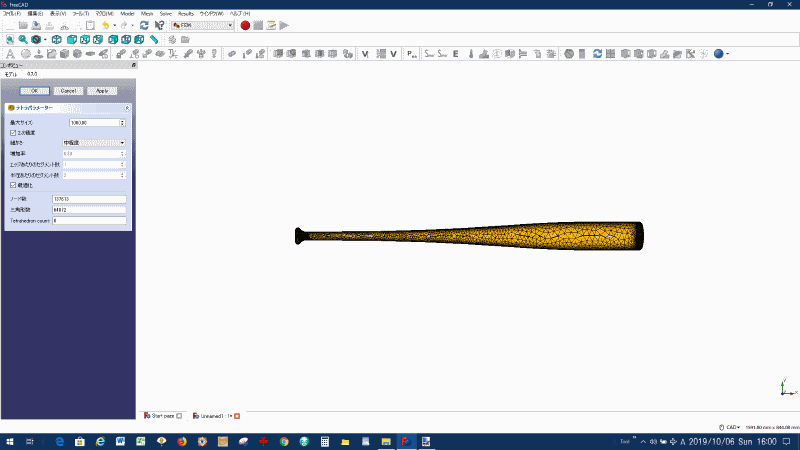
バットのメッシュ分割:中程度
図2 バットのメッシュ分割:中程度
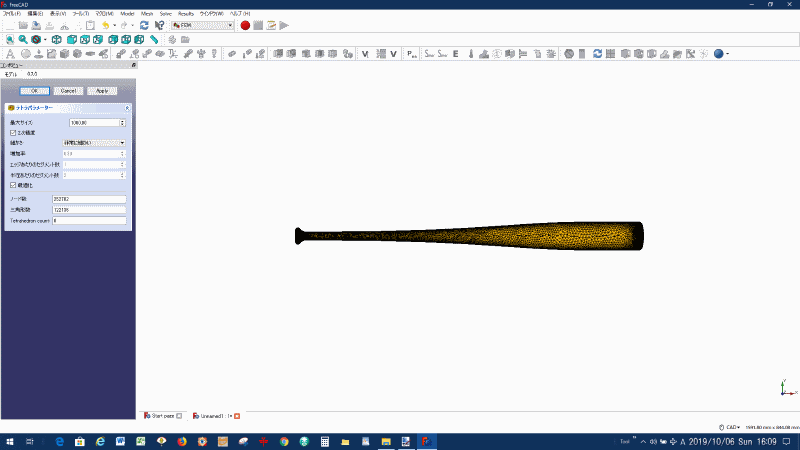
バットのメッシュ分割:非常に細かい
図3 バットのメッシュ分割:非常に細かい
メッシュが細かいほど解析精度も上がりますが、反面、
- ソルバーでの計算時間が長くなる。
- 解析結果を表示する処理が重くなる。
などの影響も出てきます。
使用するパソコンの性能(CPUの処理速度、画像表示)には限りがありますので、この要素の分割、メッシュを切る際に、解析目的に合った要素を選び、適切なメッシュサイズにすることが、解析目的を効率よく達成するためには必要です。
解析モデルの作成:形状モデルのメッシュ分割
解析モデルのメッシュ分割について、下図のような形状のモデル(解析対象の形状モデル)を、
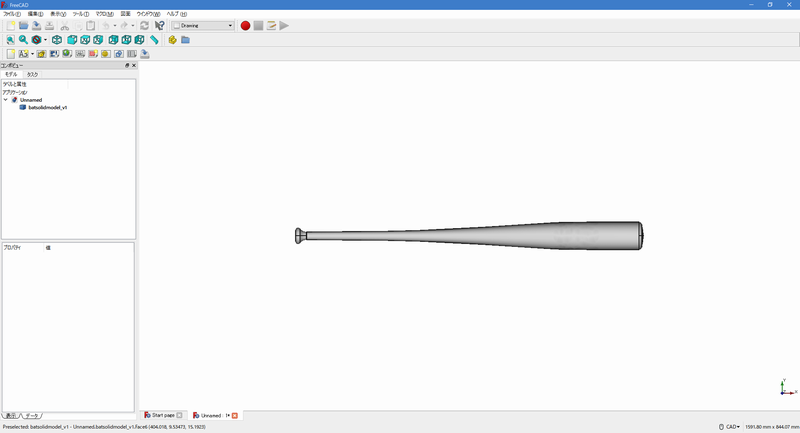
バットの形状モデル
図4 バットの形状モデル
次のような要素で分割し、
FreeCADのソリッド要素
図5 FreeCADのソリッド要素
下図のような解析モデルを作ります。
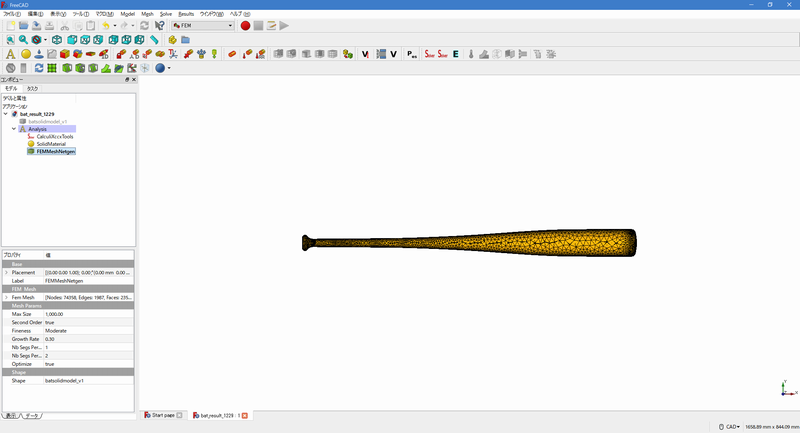
バットの解析モデル(メッシュ分割)
図6 バットの解析モデル(メッシュ分割)
解析条件を設定し、ソルバーで計算すると、次のような解析結果を得ることができます。
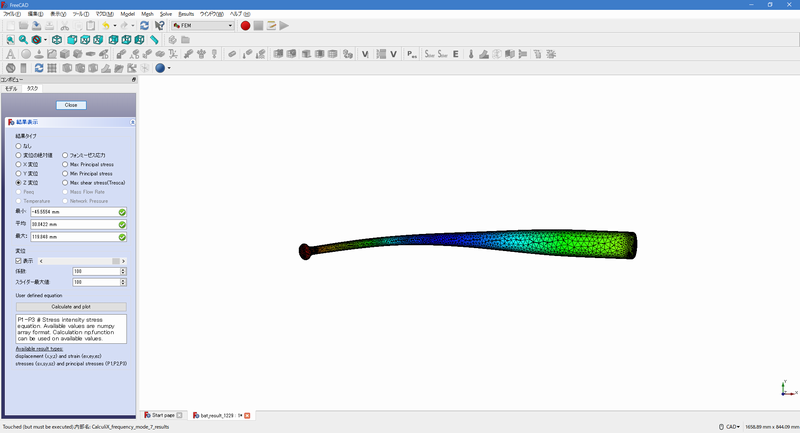
バットの固有値解析結果例(振動モード形と応力表示)
図7 バットの固有値解析結果例(振動モード形と応力表示)
メッシュを切る要素の種類
主なメッシュを紹介します。
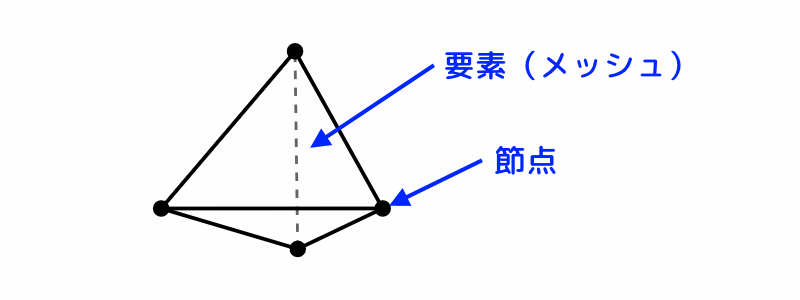
各々の要素について、中間節点がある要素は、解析精度の高い2次要素です。
中間節点とはどの様なものなのかについては、要素の説明図をご覧ください。
ビーム要素
ビーム要素は、配管(パイプ)などの解析に使用します。

FreeCAD:ビーム要素
図8 FreeCAD:ビーム要素
シェル要素
シェル要素には、三角形と四角形の要素があります。
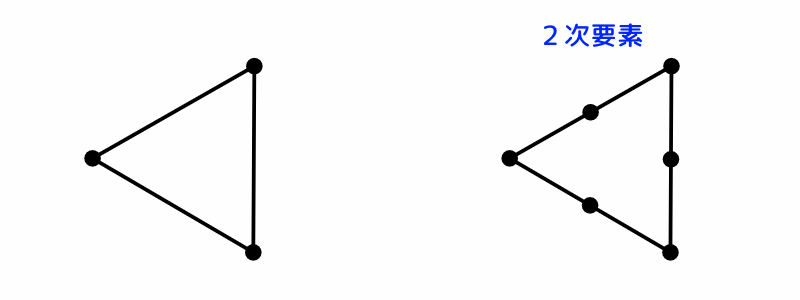
FreeCAD:シェル要素 三角形
図9 FreeCAD:シェル要素 三角形
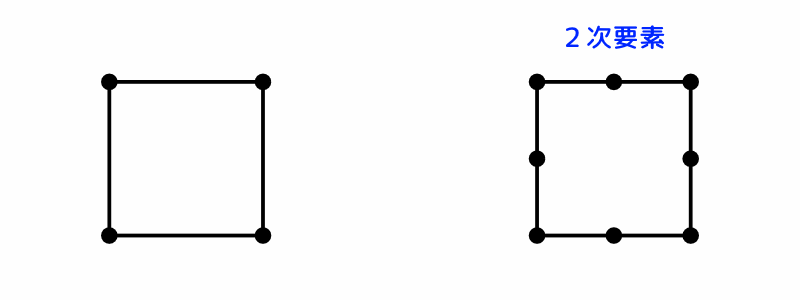
FreeCAD:シェル要素 四角形
図10 FreeCAD:シェル要素 四角形
ソリッド要素
ソリッド要素には、三角錐(テトラ)と四角錘の要素があります。
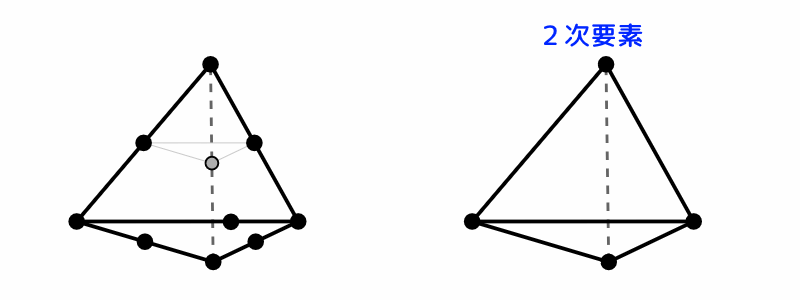
FreeCAD:シェル要素 三角錐(テトラ)
図11 FreeCAD:シェル要素 三角錐(テトラ)
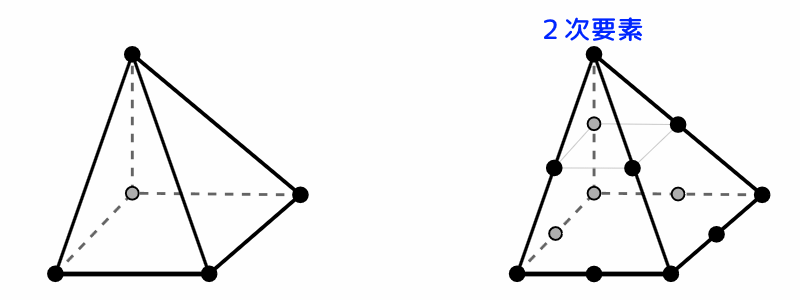
FreeCAD:シェル要素 四角錘
図12 FreeCAD:シェル要素 四角錘
メッシュと計算精度
FEMでは、要素によって計算精度が異なります。
三角形と四角形の要素とでは、四角形の要素の方が計算精度がよいと言われています。
計算精度をさらに良くするためには、メッシュの次数を上げます。
「メッシュの次数を上げる」 とは、下図の様に節点間に中間節点を入れるということです。元の要素が 「1次要素」 、中間節点を入れた要素を 「2次要素」 といいます。
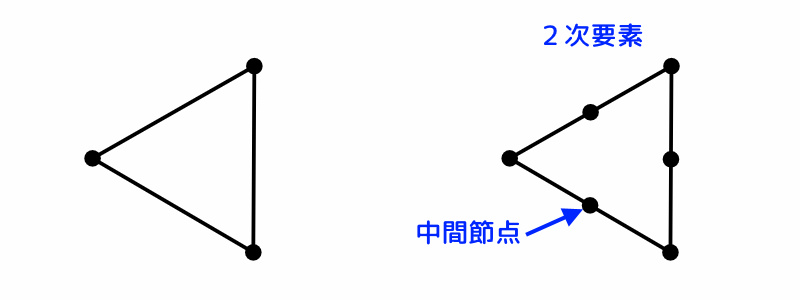
FreeCAD:シェル(三角形)の2次要素
図13 FreeCAD:シェル(三角形)の2次要素
ソリッド要素の利用
今では、3D CADでモデルを作ることが多いので、ソリッド要素を使うケースが多いと思われます。
例えば、平板の場合には、ソリッド要素のテトラではなく四角形のシェル要素を使うなど、解析対象によっては、ソリッド要素ではなくシェル要素を使うことで、計算精度と計算速度(量)を両立することができます。
メッシュ形状と解析精度
メッシュの形状は、解析精度に影響があります。
例えば、三角形要素の形状が、下図の右側の様なつぶれた三角形になっている場合には、計算精度が落ちてしまいます。
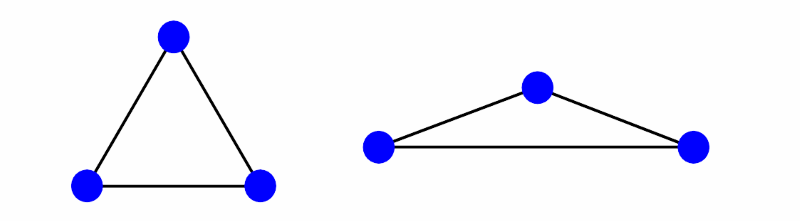
メッシュ要素の形状と解析精度
図14 メッシュの要素形状と解析精度
このような場合には、
- 部分的にメッシュを修正する。
- ちょっと面倒です。
- メッシュサイズ(=要素のサイズ)を小さくする。
- 簡単ですが、解析モデルサイズ(節点数)が大きくなってしまいます。
と改善されます。
メッシュの細かさについての考察
計算精度がよくなるということは、理論解に近くなることを意味します。
解析の計算精度に影響を与える要素には、次のようなものがあります。
- メッシュの細かさ
- メッシュを細かくすればするほど、計算精度が良くなる。
- メッシュの種類
- 三角形よりも四角形の要素の方が計算精度が良くなる。
- メッシュの次数
- 次数を上げると計算精度が良くなる。
解析の計算精度を上げると、解析時間(ソルバーによる計算時間)が長くなります。
このため、解析の精度を上げるには、解析目的に応じて次のように進めます。
- まずは、粗いメッシュで解析する。
- 得られた解析結果から、必要な解析精度に上げる。
設計や解析は、限られた期間内(納期迄)で実施することが求められます。
つまり、理論解を求める(近づける)よりも、設計としてはどの形状がより適しているかを判断するための、相対比較の解析が設計では求められるということです。
これは設計に限らず、トラブルシュートからの原因究明のための解析でも同様で、解析の目的や状況に応じた判断が必要となります。
メッシュの細かさと節点数の例
「FreeCADで始める固有値解析入門」のFreeCADによる固有値解析では、メッシュの細かさは中程度で2次要素を使っています。
下図は、メッシュの細かさとノード数(節点数)のグラフです。
グラフから、メッシュの細かさとノード数(節点数)は、比例しているのではなく、メッシュを細かくすると急激に増えていくことが分かります。
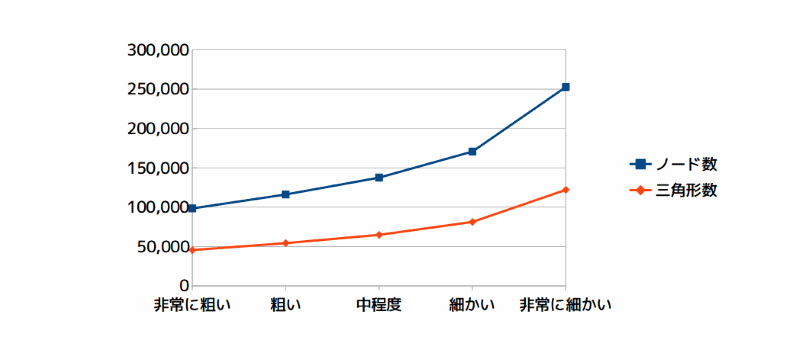
バットの固有値解析:メッシュの細かさとノード数
図15 バットの固有値解析:メッシュの細かさとノード数
ノード数が増えれば、解析時間(ソルバーの計算時間)が増えるだけではありません。
下図は下から、メッシュの細かさを「非常に粗い」、「中程度」、「非常に細かい」設定にした場合の解析モデルの図です。
メッシュを細かくして解析精度を上げると、理論解に近づきますが、同時に解析結果のデータ量も増えます。つまり、解析結果を表示したり、方向を変える際の画像処理にも時間がかかることになります。
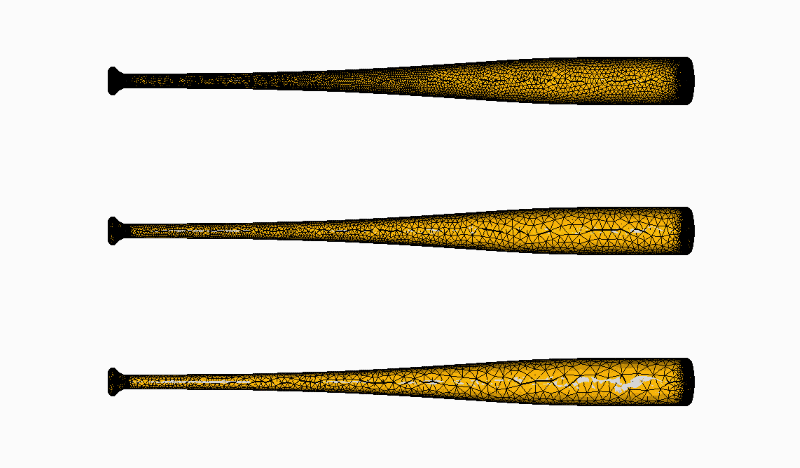
メッシュ設定(細かさ)による解析モデルの比較
図16 メッシュ設定(細かさ)による解析モデルの比較

今どきのパソコンであれば、それほど気にしなくてよいようにも思えますが、ムダに精度を高くするとムダな時間も増えますので、解析ノウハウとして適当な解析精度の目安や決め方などを残していくとよいと考えています。
まとめ
ここでは、FEM(有限要素法)により得られた解析結果を評価するために必要な、FEM(有限要素法)の基礎知識として、以下に項目について説明しました。
- 有限要素法と要素分割(メッシュ)
- メッシュを切る要素の種類
- メッシュと計算精度
- メッシュの細かさについての考察