製品設計でよく使われるFEM(有限要素法)によるシミュレーションが、応力解析です。
設計者は、使用する材料、製品の形状などの設計条件を満足できるのか、複数の設計案の中でどれがよいのかなどをFEMの応力解析で検証や比較をすることができます。
FEM(有限要素法)を使うためには、材料力学の知識が必要ですが、材料力学について勉強するとき、まずはじめに学ぶのが応力かと思います。
ここでは、FEMソフトを使う、解析結果を理解するために必要な応力についての基本的な知識について説明します。
応力とは何か?
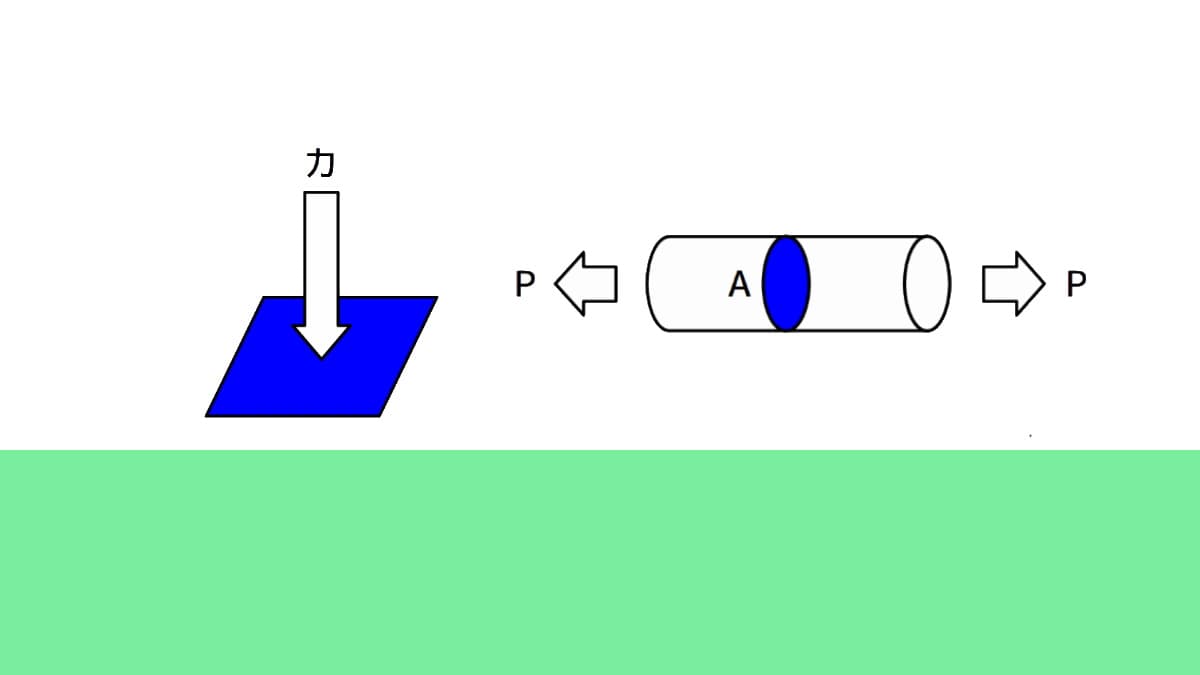
応力とは、材料(部材、部品)内に発生している単位面積あたりの力のことです。
図示してみると下図の様に、\(1 \; mm^2\)当たりにかかる力が応力です。
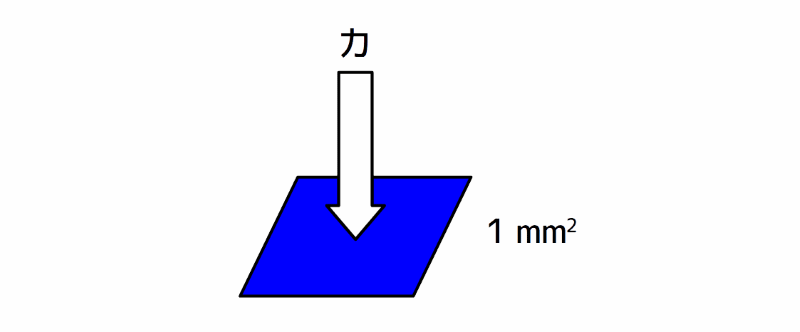
応力のイメージ
図1 応力のイメージ
部品内に発生する応力が大きくなっていくろ、やがて部材は破損(破壊)してしまいます。
下図に示すように、引張力(\(P\))を棒の断面積(\(A\))で割った値が応力となり、

丸棒に加わる応力
図2 丸棒に加わる応力
次式となります。
$$\sigma=P / A$$
ただし、
応力:\( \sigma \; (N/mm^2) \)
引張力:\(P \; (N)\)
断面積:\(A \; (mm^2)\)
例えば、断面積が\(10 \; mm^2\)の丸棒を\(100 \; N\)の力で引っ張った時に発生する応力は、次式のように求めることができます。
$$\sigma=P / A = 100 / 10 = 10 \; (N/mm^2)$$
応力についての少し詳しい説明
応力についてもう少し詳しく説明します。
下図は、図2の丸棒の断面(\(A\))の位置で切断した図になります。

丸棒に加わる応力の少し詳しい説明
図3 丸棒に加わる応力の少し詳しい説明
断面(\(A\))には、引張力(\(P\))による変形に対してこれを妨げる力として内力(\(Q\))がかかります。
内力(\(Q\))は、引張力(\(P\))に応じて生じる作用・反作用による力で、引張力と同じ大きさで逆方向の引張力であり、引張力とつり合いが取れています。
この内力(\(Q\))の単位面積当たりの力が応力\( \sigma \)です。
つまり、応力\( \sigma \)は、内力(\(Q\))を断面積(\(A\))で割った値となります。
ここで、内力(\(Q\))と引張力(\(P\))は、釣り合っていますので、次式となります。
$$Q = P$$
従って、応力\( \sigma \)、内力(\(Q\))と引張力(\(P\))との関係は、次式表すことができます。
$$ \sigma = Q / A = P / A $$
応力の単位は、力を断面積で割っているため、(\( N/mm^2 \))となります。
太さの変わる丸棒の応力の説明
下図の様に太さの変わる(断面形状が変化する)丸棒について、引張力を加えてみます。
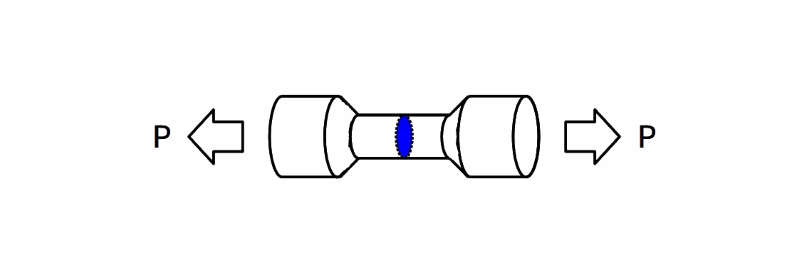
太さの変わる丸棒に加わる応力
図4 太さの変わる丸棒に加わる応力
この丸棒に引張力を加えていくと、細い部分が伸びてやがて壊れる(破断する)ことはイメージ的にも理解できるかと思います。
それでは、この壊れる部分の応力について考えてみます。
図2の丸棒の断面積が\(10 \; mm^2\)でした。
ここで、細い部分の断面積を、図2の半分の\(5 \; mm^2\)とすると、その時の応力\( \sigma \)は、次式となります。
$$\sigma=P / A = 100 / 5 = 20 \; (N/mm^2)$$
つまり、断面積が半分となり、応力は2倍になったことになります。
この結果から、次のことが分かります。
- 応力は部品の材料ではなく、形状により決まってくる。
- 形状により、応力が高くなったり、低くなったりする。
ここまで説明してきた例では、部品に引張力を加えた場合の応力は、下図の様にどの断面でも同じ応力値となるため、分かりやすいと思います。

断面と応力のイメージ
図5 断面と応力のイメージ
実際の製品設計における応力とFEM
これまでの説明での結果、形状により、応力が高くなったり、低くなったりするということが分かりました。
製品設計での応力解析とその利用については、次のようなイメージかと思います。
- 実際に応力解析をした結果、製品のある部分の応力が高すぎる場合には、形状を変えて応力を下げます。
- 逆に応力が低く設計余裕大きすぎる場合にも、形状を変更します。
これまで説明してきた丸棒のような形状であれば、部品に引張力を加えた場合の応力は、断面がシンプルなのため分かりやすく、手計算で求めることもできます。
しかし、実際の製品設計で知りたい応力は、製品を曲げる、ねじるなど、引張力などの力が均等に作用しないため、応力解析も簡単ではありません。
また、製品に加わる力の方向は様々であり、したがって内部に発生する応力も一様ではなく、部位ごとに異なるなど単純ではないことも事実です。
丸棒という簡単な部材(部品)を例に応力について説明してきました。
FEM(有限要素法)の解析結果(計算結果)をそのまま信用するのではなく、
- 応力は形状によって決まること
- 製品に加わる力は様々、同様に発生する応力も様々
であることを頭の隅に覚えておいて、FEMを利用することが大切だと考えています。
まとめ
ここでは、FEMソフトを使うための材料力学の基礎知識の1つとして、解析結果を理解するために必要な応力についての基本的な知識について以下の項目でまとめました。
- 応力とは何か?
- 応力についての少し詳しい説明
- 太さの変わる丸棒の応力の説明
- 実際の製品設計における応力とFEM