FEM(有限要素法)による応力解析に必要な材料特性には、ヤング率やポアソン比があります。
ここでは、鋼材を例にヤング率とポアソン比について説明します。
ヤング率やポアソン比についての理解を深めるためには、応力と歪(ひずみ)について理解することが必要です。
応力と歪(ひずみ)については、以下のリンク先をご参照ください。
FEMを使うために必要な基礎知識:応力とは何か
FEMを使うために必要な基礎知識:歪(ひずみ)とは何か
FEMに必要な材料特性
材料特性は、解析により様々なものがあります。
ここでは、FEMによる応力、振動解析に必要な、
- ヤング率(縦弾性係数)
- ポアソン比
について説明します。
ヤング率(縦弾性係数)
ヤング率(縦弾性係数)は、鋼材などの物を引っ張ったときの「応力」と「歪(ひずみ)」との関係を示しています。
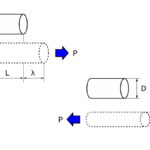
下図は、長板を長手方向に引張荷重を加えた(引っ張った)場合の、鋼材の「応力」と「歪(ひずみ)」との関係を示しています。
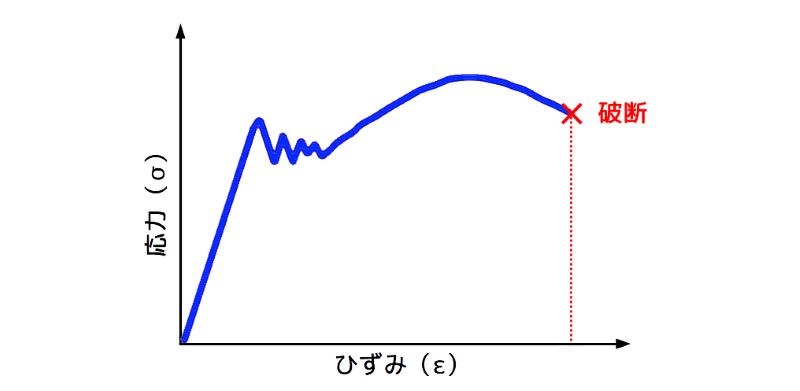
応力-歪(ひずみ)線図の一例
図1 応力-歪(ひずみ)線図の一例
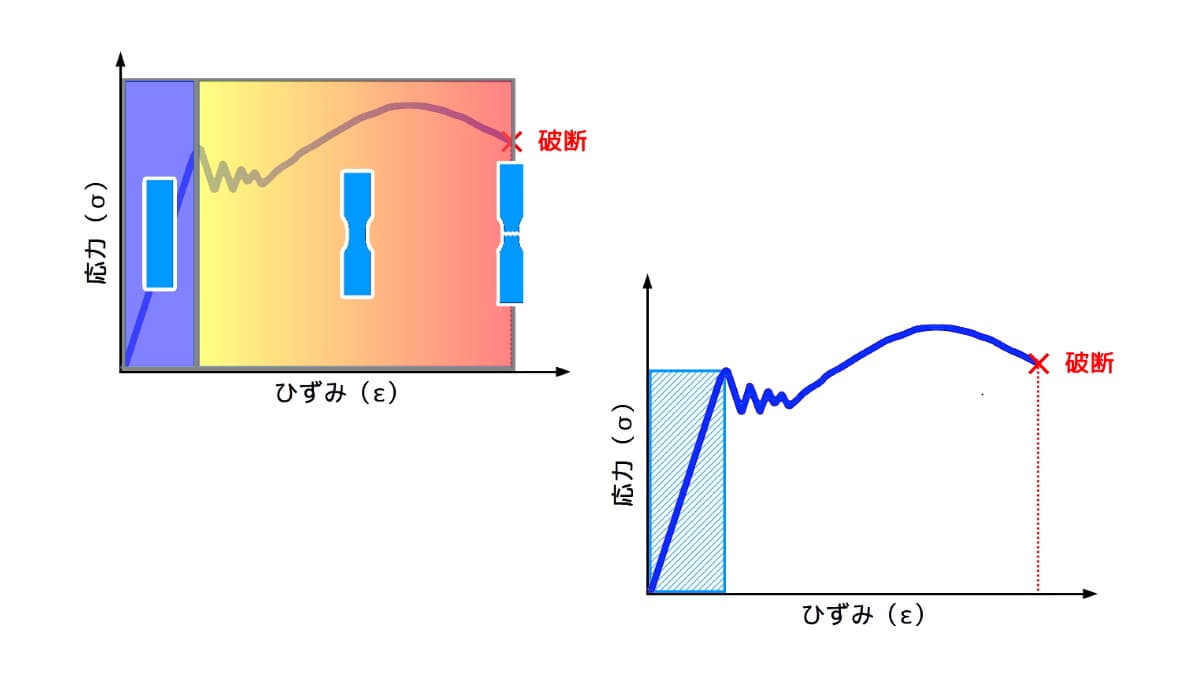
下図には、応力-歪(ひずみ)線図に、引張荷重を加えた際の板材の変形イメージを加えています。
下図の青い部分は、引張荷重を加えた場合に、「応力」と「歪」が比例関係にある弾性範囲部分です。
弾性範囲を超えて荷重を加えていくと、材料は塑性変形を起こし、元の形状に戻らなくなります。
さらに荷重を加えていくと材料は伸びてやがて破断します。
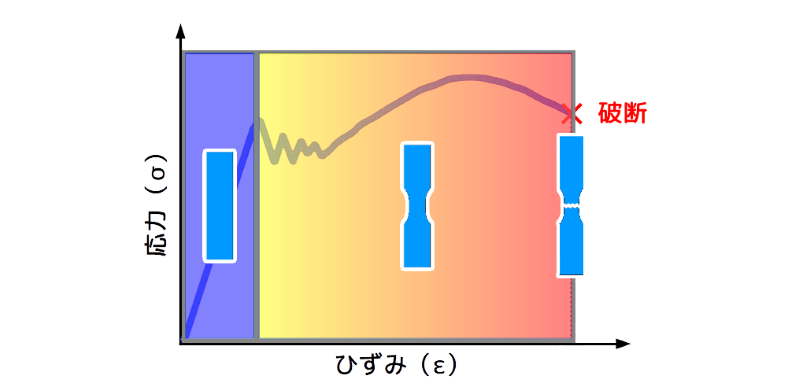
図2 応力-歪(ひずみ)線図と変形イメージ
FEMは線形解析であり、物体に引張荷重を加えた場合に、「応力」と「歪」との関係が比例関係となる範囲(弾性範囲)が解析対象となります。
下図の青の斜線部分が設計範囲であり、弾性範囲内となります。
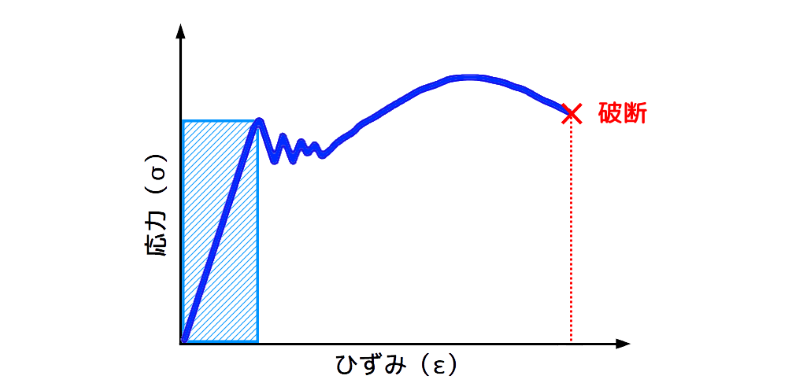
応力ー歪(ひずみ)線図と弾性範囲(設計範囲)
図3 応力-歪(ひずみ)線図と弾性範囲(設計範囲)
「弾性範囲」では、「応力」と「歪」との関係が比例関係にあるということは、次式のように、弾性範囲において、ヤング率は比例定数となることを意味しています。
$$\sigma=E \times \varepsilon$$
ただし、
応力:\( \sigma\)
ヤング率:\(E\)
歪(ひずみ):\(\varepsilon\)
したがって、ヤング率の大きさと材料との関係は、次のようになります。
- ヤング率の値が大きい = 変形しにくい材料
- ヤング率の値が小さい = 変形しやすい材料
例えば、
- 金属は、変形量(歪)が小さくても大きな応力が発生する
- ゴムは、変形量(歪)が小さいと応力がとても小さい
また、弾性範囲では、次のような特性があります。
- 引張力を大きくすると「歪」が大きくなる。
- 引張力を小さくすると「歪」が小さくなる。
- 引張力を取り除くと、荷重前(力を加える前)の状態に戻る。
参考:非線形解析とは
ちなみに、弾性範囲の範囲にない、材料の「応力」と「歪」とが比例関係にない範囲での解析は、「非線形解析」と呼ばれる別の解析となります。
引張試験で破壊まで行うと、弾性変形、塑性変形、破断へと進みますが、これを解析する場合には、線形解析と非線形解析の組み合わせとなります。

まずは、FEMによる線形解析(応力解析)について理解すればよいと考えています。
ポアソン比
ポアソン比は、引張方向に垂直な歪と引張方向の歪の比のことで、次式で表されます。
(ポアソン比)=(横歪)/(縦歪)
同じ様に引張荷重を加えた場合でも、材料により伸び方は違ってきます。このため、ポアソン比は、材料により違った値となります。
ヤング率とポアソン比の例(参考値)
ヤング率とポアソン比は、材料により異なります。
下表にヤング率とポアソン比の例(参考値)を示します。
| 材料 | ヤング率(GPa) | ポアソン比 |
|---|---|---|
| 圧延鋼 | 206 | 0.3 |
| ステンレス | 200 | 0.3 |
| アルミニウム合金 | 69 | 0.34 |
| チタン | 106 | 0.32 |
まとめ
ここでは、FEM(有限要素法)による応力解析に必要な材料特性であるヤング率やポアソン比について、以下の項目で説明しました。
- FEMに必要な材料特性
- ヤング率(縦弾性係数)
- ポアソン比
- ヤング率とポアソン比の例(参考値)