製品設計でよく使われるFEM(有限要素法)によるシミュレーションが、応力解析です。
ここでは、応力解析によく出てくる2つの応力、フォン・ミーゼス応力と主応力の基本的なことについて説明します。
応力や歪(ひずみ)については、以下の記事をご参照ください。
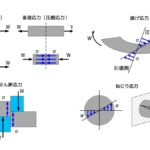
4つの応力(垂直・曲げ・せん断・ねじり)と弾性係数との関係は、以下の記事をご参照ください。
応力解析で得られる解析結果、変位と応力について
応力解析では、変位と応力の解析結果を得ることができます。
解析結果の変位からは、どの程度変形するか(変形量)が分かります。
これにより、
- 変形により製品の機能に影響が出ないか
- 設計範囲(想定した範囲)内に収まっているか
を確認することができます。
解析結果の応力からは、
- 設計範囲内の応力(許容応力)以下となっているか
- 弾性範囲に収まっているか
を確認することができます。
ここで弾性範囲について補足します。
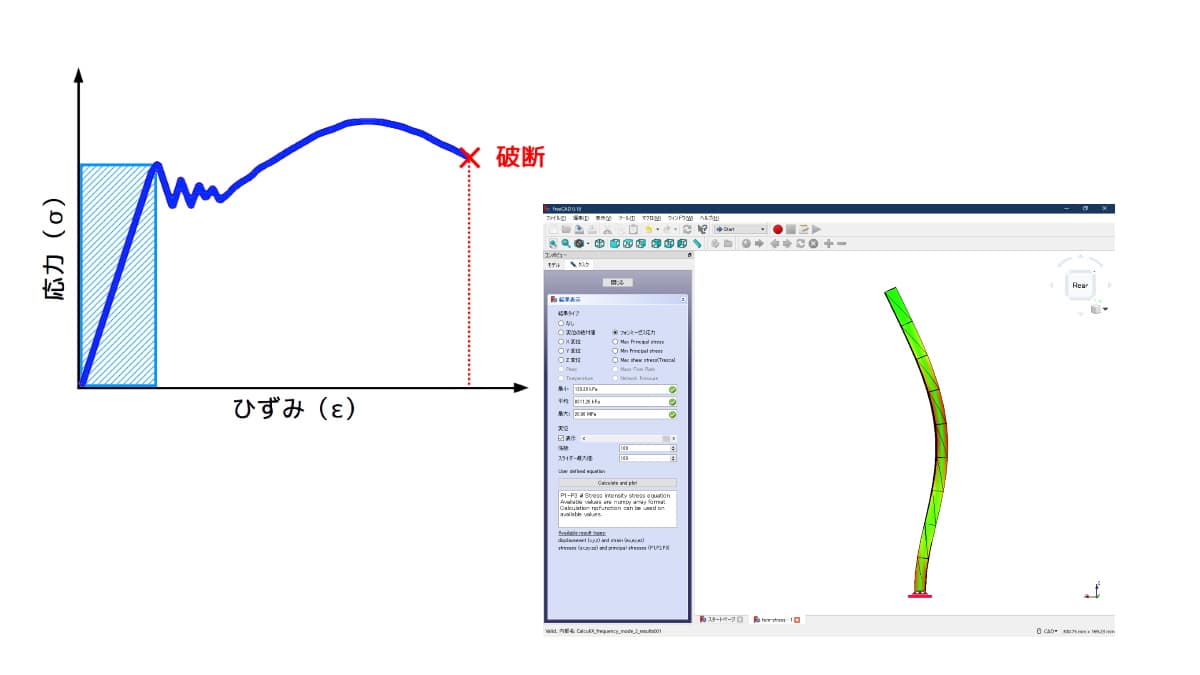
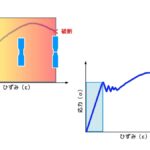
弾性範囲とは、下図の青の斜線部分に示す範囲のことで、次の様な特性があります。
- 弾性範囲内であれば、荷重を取り除くと元の形状に戻る。
- 弾性範囲を超えると、元の形状に戻らない。つまり、これが変形です。
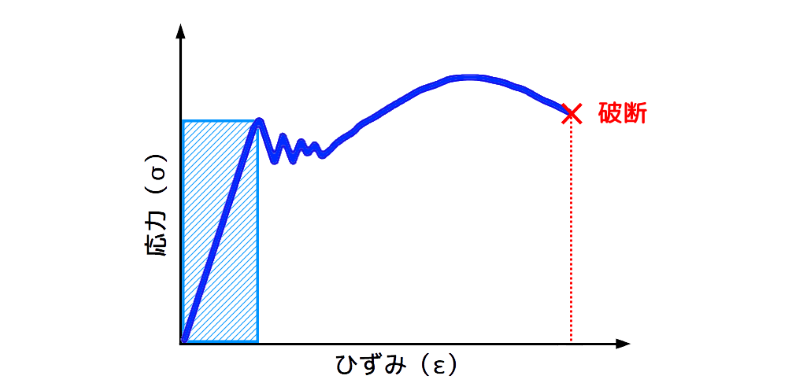
応力-歪(ひずみ)線図と弾性範囲(設計範囲)
図1 応力-歪(ひずみ)線図と弾性範囲(設計範囲)
応力の考え方(理論)について
ここでは、応力の理論について簡単に説明します。
材料の強度試験では、1軸方向、例えば上下に引張力を加えていき、材料に降伏や破断生じる力を調べます。
しかし、実際の製品では、1軸方向だけでなく、様々な方向に力が発生し、力同様応力も複雑です。
そこで複雑な応力を1軸に置き換えて評価します。
この様に、製品に発生する複雑な応力を一軸に置き換える考え方(理論)は、 「強度理論」 と呼ばれています。
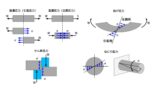
ここでは、以下の3つの強度理論についてその概要を説明します。
- 最大主応力説
- 最大せん断応力説(トレスカの説ともいいます)
- せん断ひずみエネルギー説
最大主応力説
最大主応力説では、部材の内部に発生する応力のうち、最大となる応力(主応力)が材料の強度に達した時、破損を生じると考えます。
主応力には、「大きさ」 と 「方向」 があります。
下図は、FreeCADの最大主応力と最小主応力の表示例です。
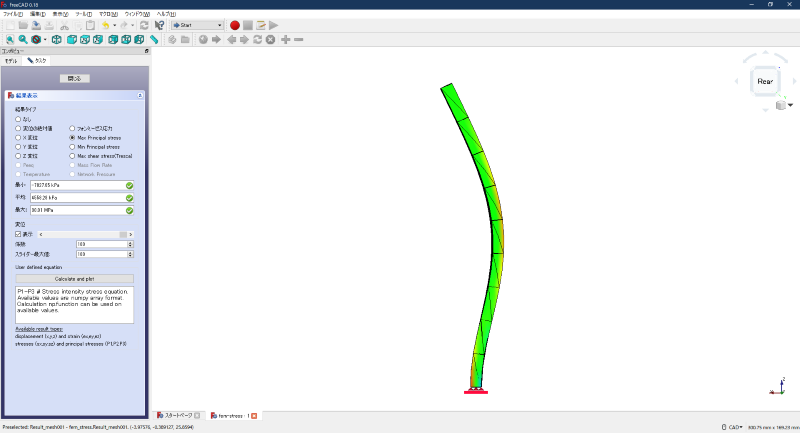
最大主応力の表示例
図2 最大主応力の表示例
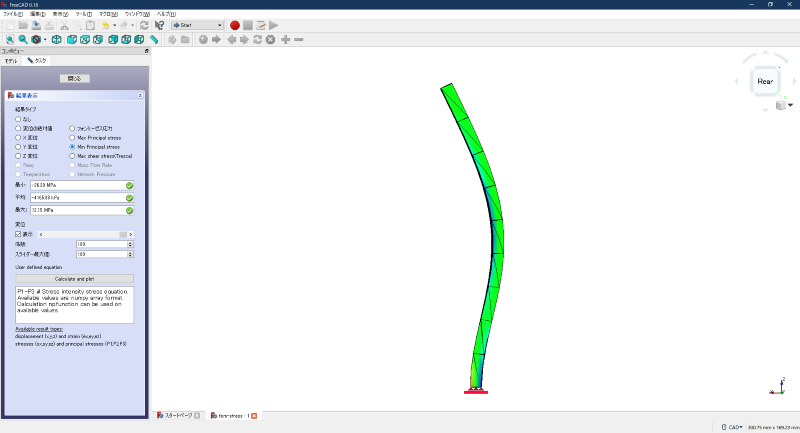
最小主応力の表示例
図3 最小主応力の表示例
最大せん断応力説
最大せん断応力説では、材料に生じる最大せん断応力が、材料の強度に達した時破損を生じると考えます。
材料によっては、他の応力よりせん断応力の方が小さい値でも、破損することがあります。
下図は、FreeCADの最大せん断応力の表示例です。
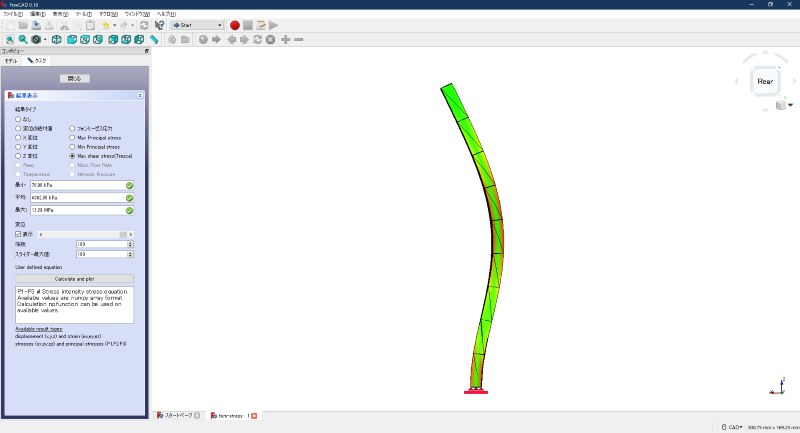
最大せん断応力の表示例
図4 最大せん断応力の表示例
せん断ひずみエネルギー説
せん断ひずみエネルギー説では、材料に蓄えられる全ひずみエネルギーのうち、体積変化を伴わないせん断ひずみエネルギーが、材料の強度に達した時に破損すると考えます。
せん断ひずみエネルギーに比例する相当応力をフォン・ミーゼス応力といい、主応力のように方向を持たない応力となります。
下図は、FreeCADのフォン・ミーゼス応力の表示例です。
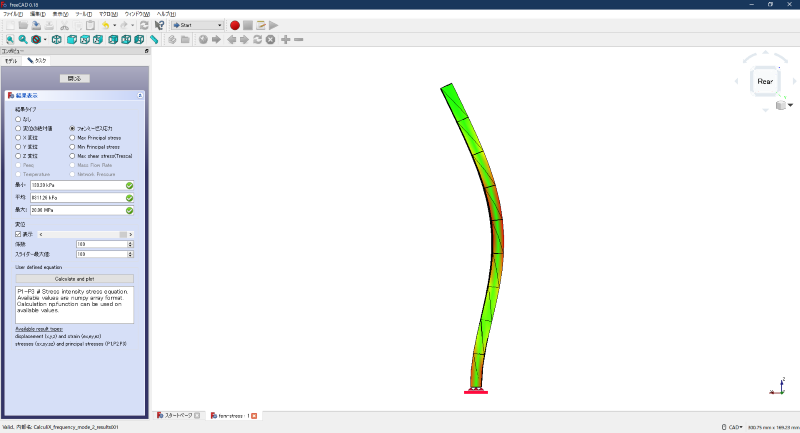
フォン・ミーゼス応力の表示例
図5 フォン・ミーゼス応力の表示例
フォン・ミーゼス応力の補足説明
材料が弾性の限界を超えても破壊されず、引き伸ばされる性質をもつ材料を延性材料といいます。
延性材料 の破損は、
「最大せん断応力説」と「せん断ひずみエネルギー説」
で評価します。
「せん断ひずみエネルギー説」は、実験結果との対応(相関)もよいことから、FEMの解析結果を評価する際によく使います。
せん断ひずみエネルギーに比例する相当応力を、フォン・ミーゼス応力といいます。
フォン・ミーゼス応力は、方向を持たない応力となります。
最大主応力の補足説明
鋳鉄(鋳物)などの脆い(もろい)性質を持つ「脆性材料」は、引張試験から得られる応力ひずみ線図がほぼ直線的で、降伏を示さずに破壊に至ります。
また、次の様な特徴があります。
- 引張強さと比較して、圧縮強さのほうが大きい
- ねじり強さは、ほぼ同じ
といった特徴があります。
そのため、脆性材料の解析には、「最大主応力説」が多く用いられています。
最大主応力は、引張応力、最小主応力は圧縮応力となります。
まとめ
ここでは、応力解析によく出てくる2つの応力、フォン・ミーゼス応力、主応力について、以下の項目で説明しました。
- 応力解析で得られる解析結果、変位と応力について
- 応力の考え方(理論)について
- 最大主応力説
- 最大せん断応力説(トレスカの説)
- せん断ひずみエネルギー説
- フォン・ミーゼス応力の補足説明
- 最大主応力について