ここでは、「振動計測(ハンマリング試験)」に必要な基礎的な知識として、
- 実験モード解析に必要なデータ
- 伝達関数の計測に必要なデータ
- センサの選定及び設置
- ハンマリングによる多点計測のポイント
について説明します。

ハンマリング試験について計測から簡易的な振動モード形の作成までを以下のページにまとめました。(2019.6.24)

実験モード解析に必要な計測データ
振動計測に限らず計測をする場合には、次の事例のように「何のために計測をするのか」という目的を明らかにすることが重要です。
事例1 対象物の振動モード形状を確認したい場合(実験モード解析)
- 計測データ:周波数応答関数(伝達関数)
- 計測方法:各計測点の伝達関数をできるだけ同一条件で計測
- FFTアナライザのチャンネル数:最低2チャンネル
事例2 対象物の実稼動状態での振動を可視化(実稼動アニメーション)したい場合(実稼動解析)
- 計測データ:パワースペクトル、クロススペクトル
- 計測方法 :多点の同時計測
- FFTアナライザのチャンネル数:計測点の数だけのチャンネル
上記は一例ですが、振動計測をする場合には、様々な目的がありそれに応じた計測データが必要になります。
だからといって、事例1や事例2のように計測の目的が定まっていれば、計測は簡単なのかと言えば、そうでもありません。
例えば、解析周波数レンジ(測定する周波数の範囲)をどの程度に設定するかは、
- 計測対象の固有振動数が何Hzなのか
- 何のためにモード解析をするのか
ということに影響を受けます。
いたずらに解析周波数レンジを高く設定すると、周波数分解能が不足し、低い周波数の振動モード形状を精度よく求めることが難しくなることもあります。
ここでの計測の目的は、「実験モード解析による振動の可視化」としましたので、FFTアナライザで計測するデータは、伝達関数(周波数応答関数)になります。
伝達関数(周波数応答関数)の計測に必要なデータ
実験モード解析に必要なデータとしては、伝達関数(周波数応答関数)があればよいのですが、正しく計測できたかどうかを確認するために、以下の計測データをFFTアナライザでモニタ(監視)します。
ここでは、伝達関数の計測時に観察する計測データ(FFTアナライザの関数)として、
- 時間軸波形
- パワースペクトラム
- 周波数応答関数
- コヒーレンス関数
について説明します。
なお、FFTアナライザで入力信号と応答信号の2チャンネルを計測する場合を例にしています。
時間軸波形
センサ(インパルスハンマと加速度センサー)の信号レベルとFFTアナライザの電圧レンジが適正かどうか判断することができます。
伝達関数の計測では、インパルスハンマを使って同じ大きさ(FFTアナライザに入力される電圧のレベル)で加振できているかどうか(再現性)を確認します。
また、ハンマリングしている本人には気づかない様なダブルハンマに気付く(検出する)こともできます。
加速度センサーの信号は、インパルスハンマで加振した対象物の振動の大きさ(FFTアナライザに入力される電圧のレベル)と振動が減衰していく様子を確認します。
振動の減衰状況は、計測時間(FFTアナライザのデータ取り込み時間)にも影響を与えるため、窓関数の設定も必要になります。窓関数については、後で説明します。
パワースペクトラム
インパルスハンマのパワースペクトラムにより、設定した周波数レンジの中で何Hzぐらいまで加振できているかを確認します。
解析に必要な周波数までフラットに加振できていることが望ましく、必要に応じインパルスハンマのチップ変更などを行います。
高い周波数になるほど加振エネルギーが不足するため、ハンマリングによる加振が回数によらず均一に加振できているかがポイントになります。
対象物によっては、振幅依存性と呼ばれ、加振力によって応答が変わるものもあります。この場合でも同一条件で加振することにより、振幅依存性の影響を小さくすることができます。
応答点(加速度センサー)との関係では、加振点とセンサ取り付け位置が最も遠い位置関係にある場合においても、十分な加振力が得られる(応答点のパワースペクトラムの観測ができる)ことが重要になります。
本番の計測に入る前に、応答点を何箇所か選んで、一定の加振力で全ての応答点において必要なパワースペクトラムを観測できるか確認します。
特に計測ポイントが多い場合には、実際の計測点よりも少ないポイントのデータで振動モード形を確認したほうが、効率的な計測と実験モード解析による可視化につながります。
周波数応答関数
周波数応答関数は、(応答点)÷(入力点)のデータです。
周波数応答関数により、ある周波数における応答点の大きさと位相を知ることができます。
- 測定周波数の範囲で何Hz(ヘルツ)が大きい等
- 位相の向き(反転)
また、平均化処理をすることで、データ精度を高めるだけでなく、正しく計測できたかどうかを周波数領域で確認することができます。
ちなみにボード線図とは、周波数応答関数の位相特性とゲイン特性を1枚のグラフにまとめたものです。
コヒーレンス関数
平均化をした場合、1回目と2回目以降のデータの相関をみて、同じようにデータが取れたかどうかを確認することができます。
コヒーレンス関数は、その性質上平均化をしないと意味がなく、コヒーレンス関数を計測する場合は、必ず平均化を行います。
センサの選定及び設置
センサを計測対象物にどのような方法で固定するかにより、センサの周波数特性が変化します。
加速度ピックアップの選定と固定法についてまとめると、以下のようになります。
- 計測試料に対して十分に軽く、小さいものを選択する
- 加速度ピックアップを取り付けることにより、計測試料の固有振動に影響を与えます。
- センサケーブルの取りまわしに注意する
- センサケーブルが対象物に接触して、減衰が変化する。
- インパルスハンマで加振したときに、ケーブルに接触してセンサの固定条件が変化し、計測データに影響が出ます。

小型のセンサは、便利なのですが、お値段もそれなりにします。
特に3軸で小型のセンサは貴重なので大切に使った覚えがあります。
センサの固定方法の一般的な長所・短所を下表に示します。
| 長所 | 短所 | |
|---|---|---|
| ワックス | 接着が簡単 |
接着度が弱い、熱に弱い。 高域の周波数まで検出不可能 |
| マグネット | 固定が簡単 | 接着度対象が限定される。 |
| 瞬間接着剤 |
固定が簡単 多種素材へ接着可能 |
計測試料を汚しやすい。 取り外す際に、センサを破壊しやすい |
| ネジ | 堅固な固定が可能 | 計測対象にピックアップ固定用のネジ穴を開ける必要がある。 |
ハンマリングによる多点計測のポイント
正確な振動モード形を得るためには、マーキングした計測点を確実にハンマリングすることが重要です。
さらに、ハンマリングによる多点計測では、
- 実験モード解析であれば、目的の振動モード形を表現できる計測点であること
- 計測点を間違えずに計測すること
- 各計測点を正確かつ一様にハンマリングすること
がポイントになってきます。
計測点のマーキングはきっちりと
多点計測では、計測点のマーキングが重要なポイントになります。
金属バットのハンマリングの様に、計測点が直線的かつ数点~10点程度であれば、ハンマリング時に計測点とハンマリングの場所が多少ずれても、計測データの大きな差となってくる場合は少ないと思います。
しかし、計測対称が平面や立体である場合、計測点数が数十点~100点を超えるようになってくると、事前に計測点のマーキング(ハンマリングする場所と計測点番号)をきっちりとしておくことが、結果的に計測・解析時間の短縮につながります。
振動モード形を表せる計測点を選ぶ
計測点は、実験モード解析での振動モード形表示の形状モデルの座標点となるため、観測したい振動モード形をイメージして選定します。
が、まずは少ない計測点、計測回数でハンマリングを行い、どのような振動モード形をしているかのイメージをつかみます。
次に、詳しく観察したい部分の計測点を増やして、ハンマリングを行います。
FEMの固有値解析の利用
FEMの固有値解析による振動モード形状を利用して、計測点を決めていくこともできます。
この際、FEMの振動モード形状そのものを正確にハンマリング試験の計測点で表すのではなく、観察したい振動モード形状を表すことができる計測点を選ぶことがポイントになります。
基本的なモード形状については、以下をご参照ください。
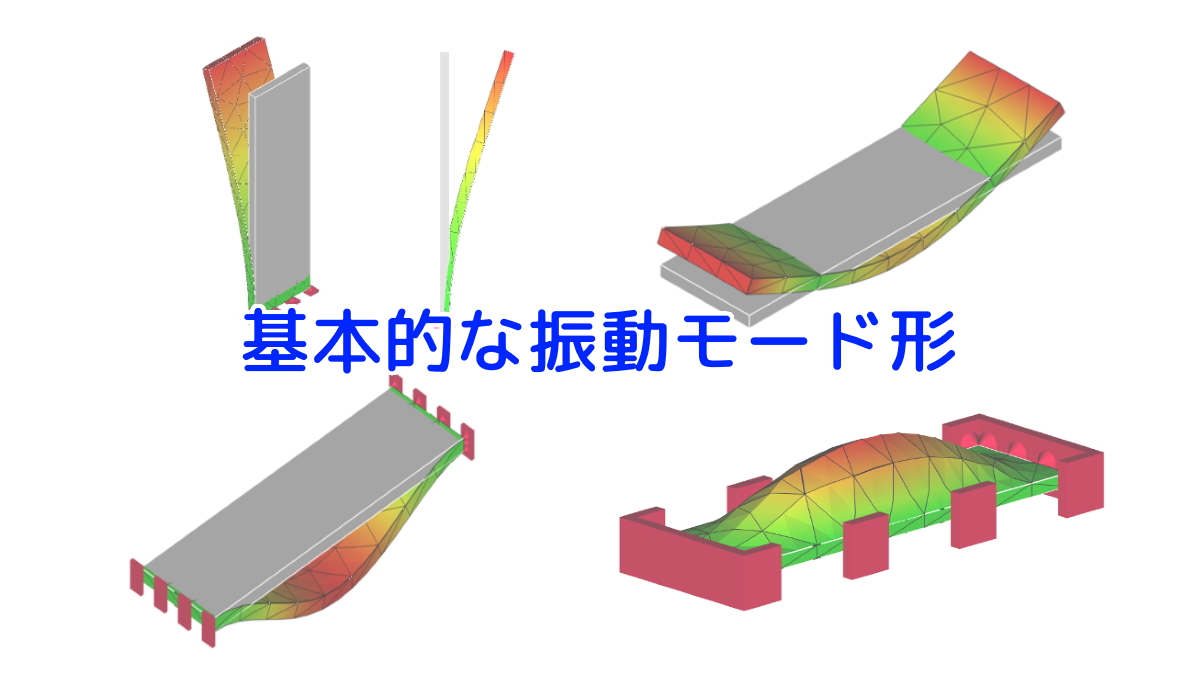
レーザースキャニング装置による多点計測
多点計測では、ハンマリング以外に、レーザースキャニング装置を使う方法もあります。
解析モデルと計測点の対応についてはハンマリングと同様ですが、計測点数については、計測時間がハンマリングに比べ圧倒的に短いためそれほど気にする必要はありません。
というとメリットばかりのようですが、レーザースキャニング装置を使う場合、加振装置も併用することになるため、計測も大掛かりになりがちですし、何よりも費用対効果がネックになるかとが多いかと思います。
まとめ
ここでは、ハンマリング試験に必要な基礎的な知識として、振動計測(ハンマリング)の手順について、以下の内容について説明しました。
- 実験モード解析に必要な計測データ
- 伝達関数(周波数応答関数)の計測に必要なデータ
- 時間軸波形
- パワースペクトラム
- 周波数応答関数
- コヒーレンス関数
- センサの選定及び設置
- ハンマリングによる多点計測のポイント


