梁の強さと断面形状について、以下の記事でまとめました。

断面係数は、断面二次モーメントと似ていて、曲げモーメントに対してどれだけ抵抗できるかを意味しており、次の様に使い分けます。
- 断面二次モーメントは、梁の変形のしにくさを表す。(曲がりにくさ、たわみ)
- 断面係数は、梁の曲げの強さを表す。(応力に対する強さ)
ここでは、梁の断面係数と断面二次モーメントについて図と計算式で説明します。
断面二次モーメントとは
梁の曲りづらさと強さは、梁の断面形状によって決まります。
そして、断面二次モーメントは、断面の強さに関係していて、材料の断面の性質の一つでもあります。
ここで、材料の曲がりにくさについて考えてみます。
木材や鉄などはゴムよりも曲がりにくい材料です。
同じ「曲げる」ことをしても、材料(金属、木材、プラスチック、ゴムなど)により、曲がりやすかったり、曲がりにくかったり、材料によっては曲がらずに折れたりします。
この「曲がりにくさ」は材料によって決まるものです。
この材料の曲がりにくさの指標としては、材料の定数(ヤング率)があります。
また、同じ材料でもその断面の形状によって曲がりにくさは異なります。
例えば、断面積の広さ(大きさ)により、材料の曲がりやすさ、曲がりにくさは異なります。
- 例 1枚の板より、2枚の板を重ねた場合のほうが曲がりにくい。
また、同じ断面積でも、断面の形状により材料の曲がりやすさ、曲げにくさは異なります。
- 例 梁の縦置きと横置き
断面二次モーメントは、曲げモーメントに対して材料がどのくらい耐えることができるのかを判断するために使われます。
縦(\(h\))、横(\(b\))の下図に示す長方形の断面二次モーメント(\(I\))は、次式で表されます。
$$I = \frac 1 {12} b h^3$$
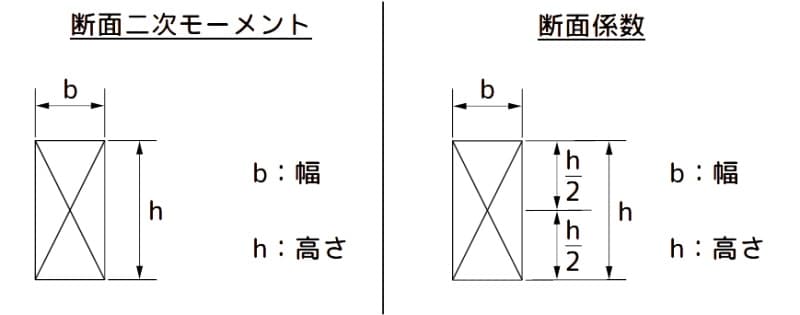
断面二次モーメントと断面係数の諸元
図1 断面二次モーメントと断面係数の諸元
断面二次モーメントとたわみ
下図の様に梁に力を加えると、梁は変形します。この変形(図2では下方向への変形)が、たわみです。
梁に力を加えてたわみが生じている時、梁に加わる力と曲げモーメント下図の様になります。曲げモーメントは、下図の様に梁の両側で同じ様に発生しています。
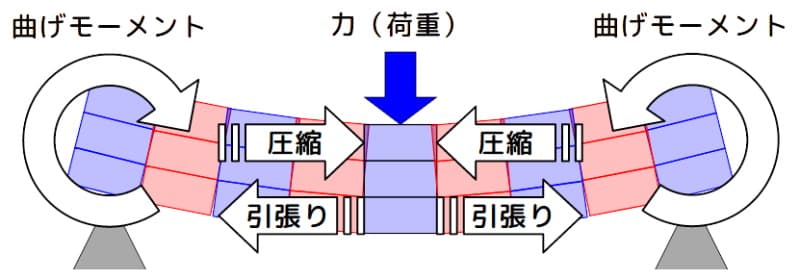
梁に力を加えた時の曲げモーメントのイメージ
図2 梁に力を加えた時の曲げモーメントのイメージ
この時、断面二次モーメントは、変形のしにくさを表しており、変形(たわみ)が小さいと断面二次モーメントの値も小さくなります。逆に断面二次モーメントの値が大きいほど、変形しにくい(たわみにくい)ということです。
つまり、断面二次モーメントは、変形のしにくさ(曲がりにくさ)を表す値と言うことになります。
縦(\(h\))、横(\(b\))の下図に示す長方形の断面二次モーメント(\(I\))は、次式で表されます。
$$I = \frac 1 {12} b h^3$$
断面係数とは
断面係数とは、文字通り断面に関する係数です。
同じ断面積の材料でも、断面の形状によって曲がりにくさは異なります。
断面係数は、断面二次モーメントと同じような意味であり、曲げモーメントに対してどれだけ抵抗できるかを意味しています。
つまり、断面係数は、曲げに対する強さを表し、断面係数が大きい方が曲げに対して強いということになります。
また、断面係数は、上述の断面二次モーメントを使い求めることができるのですが、まずは断面係数の公式から説明します。
断面係数(\(Z\))は、次式となります。
\(Z\) = (図心を通る軸についての断面二次モーメント(\(I\)))/(図心軸から縁までの距離)
ここで、図3を再掲して、断面係数について説明します。

断面二次モーメントと断面係数の諸元
図3(再掲) 断面二次モーメントと断面係数の諸元
図心とは、上図の長方形の中心点のことです。
断面係数(\(Z\))の右辺の分子は、断面二次モーメント(\(I\))です。
断面係数(\(Z\))の右辺の分母の「図心軸から縁までの距離」は、上図の長方形中心から長方形の上辺か下辺のことです。
つまり、
$$図心軸から縁までの距離 = \frac h 2$$
となります。
これを、上述の断面係数(\(Z\))に代入して整理すると、次式となります。
$$Z = \frac I {\frac h 2} = \frac {\frac 1 {12} b h^3} {\frac h 2} = \frac 1 {6} b h^2$$
断面二次モーメントと断面係数のまとめ
断面二次モーメントと断面係数は、どちらも梁の強さに関連していますが、次の様な違いがあります。
- 断面二次モーメントは、梁の変形のしにくさを表す。(たわみ量)
- 断面係数は、梁の曲げの強さを表す。(応力に対する強さ)
まとめ
断面係数は、断面二次モーメントと似ていて、曲げモーメントに対してどれだけ抵抗できるかを意味しており、次の様に使い分けます。
- 断面二次モーメント:梁の変形のしにくさを表す。(曲がりにくさ、たわみ)
- 断面係数:梁の曲げの強さを表す。(応力に対する強さ)
ここでは、梁の断面係数と断面二次モーメントについて、以下の項目で説明しました。
- 断面二次モーメントとは
- 断面二次モーメントとたわみ
- 断面係数とは
- 断面二次モーメントと断面係数のまとめ


