FEM(有限要素法)による応力解析に必要な材料特性には、ヤング率やポアソン比があります。
ヤング率やポアソン比についての理解を深めるためには、応力と歪(ひずみ)について理解することが必要です。
ここでは、歪(ひずみ)についての基本的な知識について説明します。
歪(ひずみ)とは何か?
例えば、棒を引っ張ると伸びます。
この伸びた量を変形量とすると、歪(ひずみ)とは、棒の元の長さに対する変形量の割合(比率)のことです。
縦歪(ひずみ)
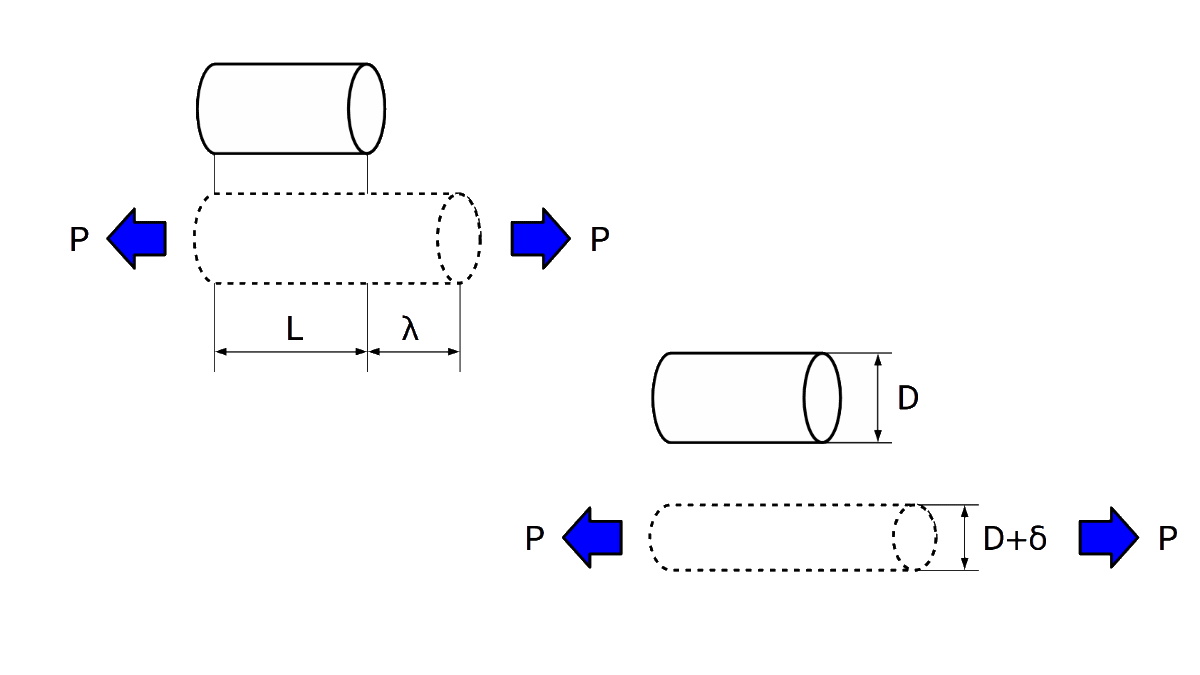
下図の丸棒を例に、説明します。
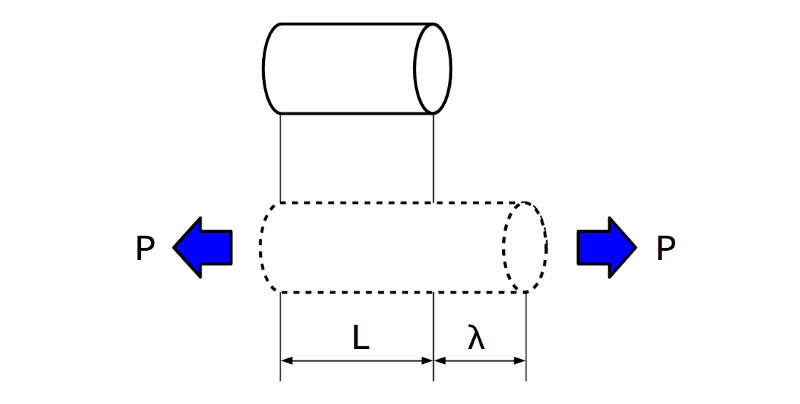
引張方向の歪(縦ひずみ)
図1 引張方向の歪(縦ひずみ)
上図において、各記号は以下の通りです。
丸棒の元の長さ:\(L\)
丸棒を引っ張ったときに伸びた量(変形量):\( \lambda \)
歪は、元の長さに対する変形量で、次式で表すことができます。
$$\varepsilon = \lambda \; / \; L $$
この、引張り方向のひずみを 「縦ひずみ」 といいます。
横歪(ひずみ)
横ひずみは、引張り方向に垂直なひずみです。
下図の丸棒で説明します。

引張方向に垂直な歪(横ひずみ)
図2 引張方向に垂直な歪(横ひずみ)
上図において、各記号は以下の通りです。
丸棒の元の直径:\(D\)
丸棒を引っ張ったことによる縮んだ量(変形量):\( \delta \)
引張り方向に垂直な方向では、棒は縮みます(細くなります)。
この縮み量\( \delta \)を元の径\(D\)で割った値が「横ひずみ」\( \varepsilon \)となり、縦ひずみと同様次式で表すことができます。
$$\varepsilon = \delta \; / \; D $$
ポアソン比
丸棒であれば、棒の長手方向(縦方向)に伸びると、これに垂直な方向(棒の直径方向)には縮みます(細くなります)。
下図に、ゴム板のような長方形の板を長手方向に引っ張った場合のイメージ図です。
長手方向に引っ張ると短手方向には縮むことをイメージしています。
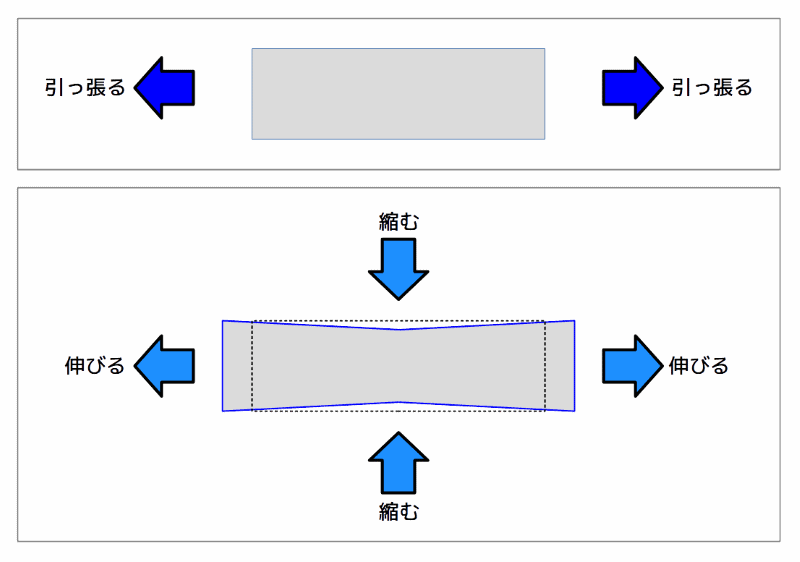
長手方向に引っ張った場合のゴム板の変形イメージ
図3 長手方向に引っ張った場合のゴム板の変形イメージ
この長手方向に伸び、短手方向に縮む関係が、ポアソン比です。
ポアソン比(\( Y \))は、縦ひずみと横ひずみから求めることができます。
\( Y \) = (横ひずみ)/(縦ひずみ)
ポアソン比は、材料によって異なりますが、伸びやすい材料ほどポアソン比が大きくなる傾向にあります。
代表的なものを以下に列挙しますが、FEMソフトには材料特性として主な材料のポアソン比は組み込まれていて選べるようになっています。
| 材料 | ポアソン比(例) |
|---|---|
| 鋼 | 0.34 |
| 鋳鉄(鋳物) | 0.27 |
| 銅 | 0.343 |
| アルミニウム | 0.345 |
| コンクリート(参考) | 0.2程度 |
| ゴム(参考) | 0.49程度 |
圧縮歪(ひずみ)
圧縮歪は、引張歪と同じ様にして求めることができます。
下図の丸棒で説明します。
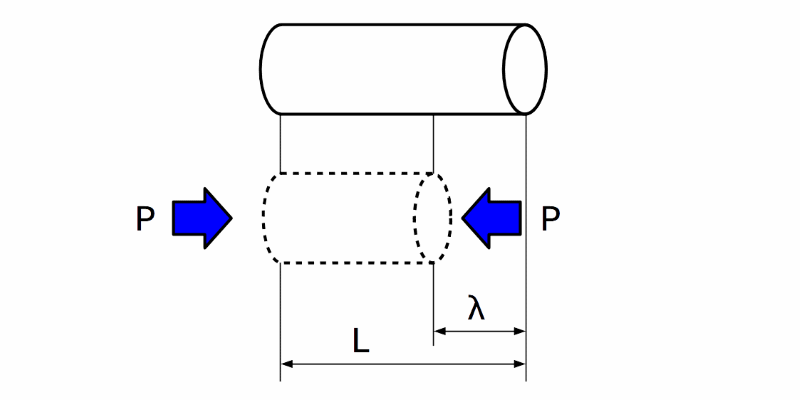
圧縮歪(ひずみ)
図4 圧縮歪(ひずみ)
上図において、各記号は以下の通りです。
丸棒の元の長さ:\(L\)
丸棒を圧縮したことによる縮んだ量(変形量):\( \lambda \)
丸棒を圧縮すると、引張と逆方向に荷重が加わります。
圧縮歪(\( \varepsilon \))は、次式で表すことができます。
$$\varepsilon = \lambda \; / \; L $$
せん断歪(ひずみ)
下図の様に、ある物体に力を加えた場合、その物体の一部を取り出してみると、ひし形に変形しています。
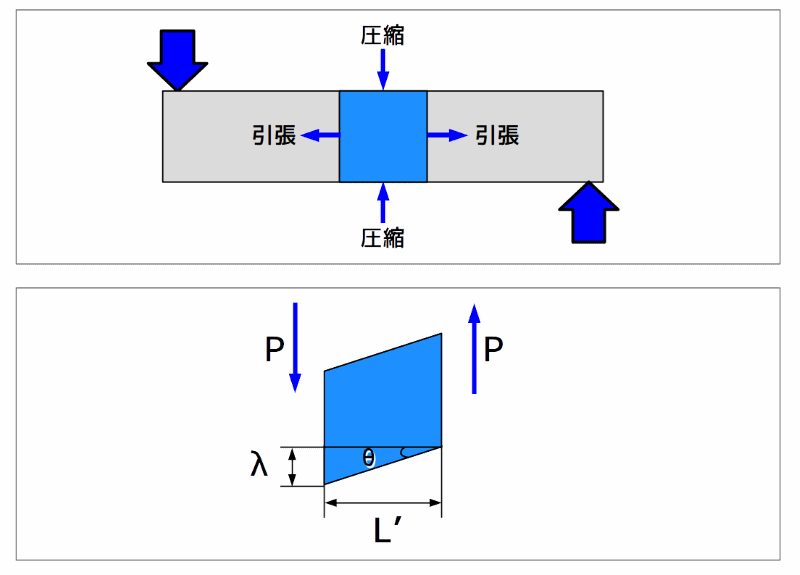
せん断歪(ひずみ)
図5 せん断歪(ひずみ)
上図において、各記号は以下の通りです。
せん断力を受けている微小距離:\(L’\)
せん断変形量:\( \lambda \)
せん断によりずれた角度:\( \theta \)
せん断歪(\( T \))は、次式で表すことができます。
$$T = \lambda \; / \; L’ $$
上式の\( \lambda \; / \; L’ \)は、図5より\( tan \theta \)となります。
せん断によりずれた角度(\( \theta \))は、微小角度であるため、次式の関係となります。
$$ tan \theta = \theta$$
従って、せん断歪は、せん断によりずれた角度(変形した角度)と等しくなります。
まとめ
FEM(有限要素法)による応力解析に必要なヤング率とポアソン比についての理解を深めるためには、応力と歪(ひずみ)についての理解が必要です。
ここでは、歪(ひずみ)についての基本的な知識について、以下の項目で説明しました。
- 歪(ひずみ)とは何か?
- 縦歪(ひずみ)
- 横歪(ひずみ)
- ポアソン比
- 圧縮歪(ひずみ)
- せん断歪(ひずみ)