ここでは、振動制御について、制御系設計に必要な制御理論やモデリングについて説明します。
何か具体的な制振の例(イメージ)があった方が分かりやすくなると思いますので、まずは事例を紹介します。
振動制御の例:超高層ビル、長大橋
振動制御の例として、超高層ビル(塔状構造物)と長大橋の制振について紹介します。
超高層ビルの制振
超高層ビルにおいて、強風や地震に耐える構造的な強さは当然必要ですが、高層階は眺望の良さなどの付加価値が高い反面、風などの外乱により高層階ほど揺れが大きいという問題があります。
このため、制振(振動制御)により積極的に揺れを抑えることで、眺望がよく快適な空間、住居やホテルなどにも利用できるようになります。
長大橋の場合
大きな橋を建設する場合、当然ながら初めのうちは橋脚がタワーの様に単独で建設されます。
橋脚は、長大橋として完成すれば構造的に強くなりますが、建設中は風などの外乱に弱い状態で、建設作業にも影響が出てきます。そこで、振動制御で橋脚の揺れを抑えるため制振装置を設置します。
このような目的のため設置された制振装置は、長大橋の完成後でも有効に機能するためそのまま使われているそうです。
では、実際に振動制御をするために何をするのか、制御系設計とモデリングについて説明します。
制御系設計とモデリングとの関係
振動制御をするためには、制振対象のモデリングと制御系設計が必要となります。
制御系設計とモデリングとの関係は、下図のようになります。
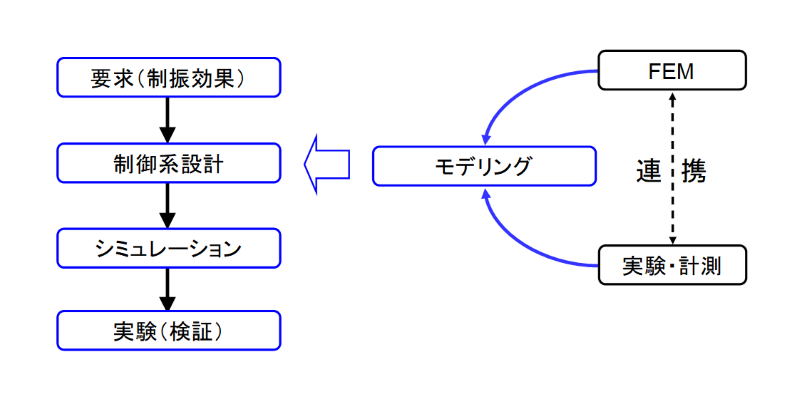
制御系設計とモデリング
上図の各プロセスについて説明します。
要求(制振効果)
振動制御をする目的、どの程度の制振効果を得るか目標値を決めます。
例えば、
- 超高層ビルや長大橋などの建築物であれば、過度な制振は制振対象の構造そのものへのダメージになりますし、突発的な地震と風による対策とでは要求が違ってきます。
- 工作機械の加工精度を維持するために、できるだけ大きな制振効果を得たい場合もあります。
- アクティブ・サスペンションであれば、制振に使うエネルギー(動力)を抑えたいという要求もありそうです。
モデリング
このブログでは、振動モード形の節を利用したモデリングを使っています。
振動モード形の節を積極的に利用したモデリング、「不可制御・不可観測性を利用した低次元化モデル作成法」は、私も研究生時代に使っていました。
このため、FEM(有限要素法)の固有値解析と実験モード解析の結果から、制振対象のモデルを作成します。
制御系設計とシミュレーション
現代制御理論の1つであるLQ制御を使い状態フィードバックを実現します。
シミュレーショにより、フィードバックゲインを調整します。
実験(検証)
実験によりシミュレーション結果を検証します。
次に、制御理論についての簡単な説明と、制御系設計についてもう少し詳しく説明します。
古典制御から現代制御理論による制御系設計
ここで、制御系設計にはかかせない、制御理論の一部について説明します。
古典制御理論の代表PID制御
古典制御理論の代表は、PID制御です。
PID制御(Proportional-Integral-Differential Controller)は、以下のPIDという3つの要素、
- 比例(Proportional)
- 積分(Integral)
- 微分(Differential)
を使った制御のことです。
この3つの要素を調整することで、1入力1出力の制御系を設計することができます。
現在でも産業界では主力の制御系だと言われています。
現代制御理論による多入力多出力系の制御系設計
今では(だいぶ前からですが)、多入力多出力系の制御系設計が必要とされ、実際の制御系にも現代制御理論が使われるようになっています。
現代制御理論を使った制御系設計は、多入力多出力系の制御系を設計ツールを使って簡単に行うことができます。
ざっくりとまとめてしまうと、制振対象の運動方程式を立てれば、現代制御理論を使った安定性の保証された制御系を設計できるということです。
現代制御理論による最適制御手法は他にもありますし、ポスト現代制御理論なるものも出ていますが、本質的には、制御系の安定性を確保(保証)したうえで、どの様な制振効果を得るかを設計することに変わりはないと考えています。
また、実際の構造物や機械に組み込むためには、制振効果だけでなく、
- 実際の制御プログラムの制御器(コントローラ)のプログラムのサイズ
- 制御プログラムを動かすデバイス(DSP、組込用CPUなど)
- 制振装置(制御用アクチュエータ)の信頼性
- 維持管理(メンテナンス)を含むコスト(ライフサイクルコスト)
なども考慮することになります。
制振装置の設計は、
- 机上のシミュレーション
- 実験による理論検証
- 実機モデルによるシミュレーションと実験(試験)
を経て、
- 試験運用
- 実運用
となるのですが、ユーザーとしてはこれらを意識することはほとんどないと思います。
また、制振効果を感じる機会もほとんどないと思います。
制振装置のON/OFFを体験できる機会があれば、制振効果について感じることもできるでしょうが、メンテナンスでもない限り経験することはないと思うからです。
こういった意味では、制振はインフラの一部となっていると考えています。
次項でモデリングと制御系設計について説明します。
LQ制御による2自由度系の制御系設計
例えば、現代制御理論の1つであるLQ制御を使い2自由度系モデルのフィードバック制御系を設計(2入力1出力の制御系)する流れは、次のようになります。
LQR:Linear Quadratic Regulator
まず、制振対象の2自由度系のモデルを作成します。
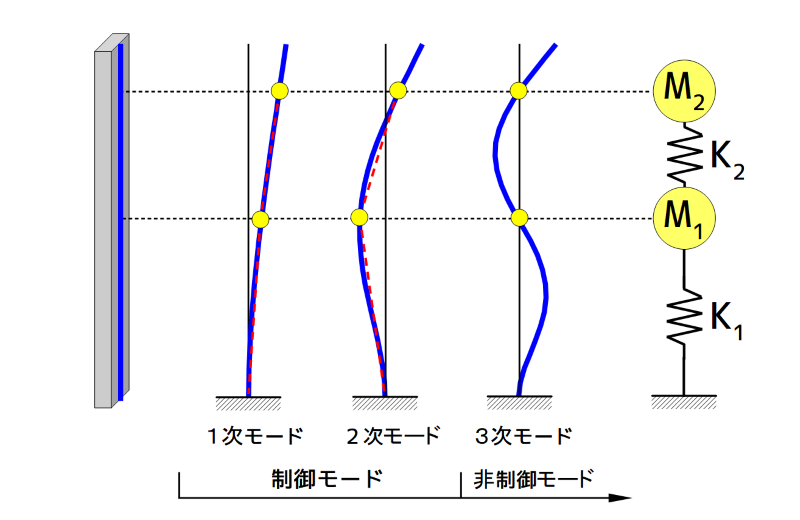
制振対象の2自由度系のモデル作成イメージ
- 制振対象の2自由度系モデルと制振装置1自由度系の運動方程式を立てます。
- 運動方程式を状態方程式に変換します。
- 運動方程式と状態方程式は、表記方法が異なるだけで展開すれば同じ内容です。
- LQ制御系を設計します。
ここでは、状態フィードバックを行います。
- 評価関数を最小にするフィードバックゲインを求めます。
- LQ制御では、線形2次形式の評価関数を使います。
- 制御系の安定性は、最適制御理論により保証されています。
- 制御系(制振効果)の調整をします。
- 評価関数の重み係数により簡単に調整できます。
- 重み係数には、QとRがあります。
- 重み係数Qは、制御特性を調整します。
- Qには、運動方程式の速度項と変位項にかかる重み係数があり、どのような制御をかけるか調整することができます。
- Rは制御量を調整します。
- フィードバックゲインを求めるために、Riccati方程式を解きます。
- MATLABやScilabで簡単に求めることができます。
実験によるシミュレーション結果の検証
実験によりシミュレーション結果の検証をします(モデルの検証でもあります)。
これらの一連のシミュレーションは、制御系ツール(MATLABやScilab)を使うことで簡単に行うことができます。
身近にある振動や振動対策については、以下をご参照ください。
まとめ
ここでは、振動制御について、制御系設計に必要な制御理論やモデリングについて、以下の項目を説明しました。
- 振動制御の例:超高層ビル、長大橋
- 制御系設計とモデリングとの関係
- 古典制御から現代制御理論による制御系設計
- LQ制御による2自由度系の制御系設計
- 実験によるシミュレーション結果の検証