柔軟構造物の低次元化モデル作成法：質量と剛性パラメータ

「振動モード形を利用したモデリング入門」の「柔軟構造物の低次元化モデル作成法」では、

質量パラメータを使った固有モード修正による２質点系モデル作成法

について説明しました。

ここでは、

質量と剛性パラメータを使った固有モード修正による２質点系モデル作成法

について説明します。

柔軟構造物の低次元化モデル作成法（質量と剛性パラメータによる固有モード修正）
質量・剛性パラメータによる２質点系モデル作成法
- 平行板ばね構造物の２自由度系モデル作成例
まとめ

柔軟構造物の低次元化モデル作成法（質量と剛性パラメータによる固有モード修正）

モード座標系と物理座標系との関係を活用すると、分布定数系の固有モードを集中定数系の固有モードに修正して、柔軟構造物の任意の点を質点とする低次元化モデルを作成することができます。

参考：「振動モード形を利用したモデリング入門」

ここでは、

質量と剛性パラメータを使った固有モード修正による２質点系モデル作成法

について説明します。

質量・剛性パラメータによる２質点系モデル作成法

低次元化モデルを作成する際に、質量集中の条件に加え、仮定したばねマスモデルに、質量・剛性行列を共に整合させる手法について説明します。

下図は、質量・剛性パラメータによる２質点系モデル作成法のイメージを示しています。

同図の左から、制振対象、制振対象の１次〜３次の振動モード形、及び、２個の質点と２個のばねからなる低次元化モデル（２自由度系モデル）です。

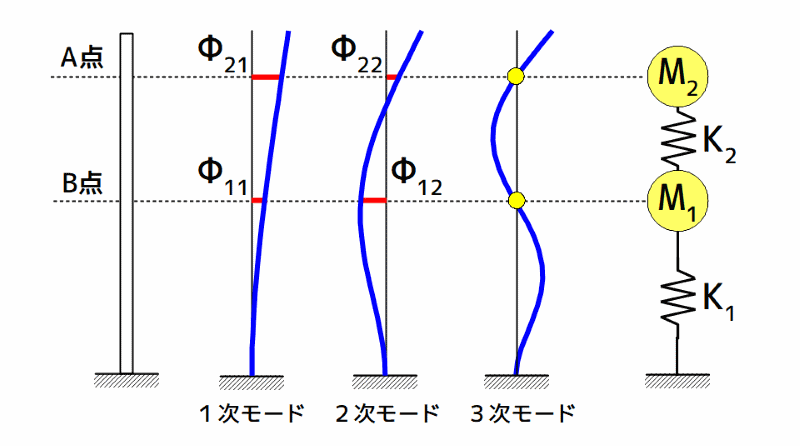
質量・剛性パラメータによる２質点系モデル作成イメージ

図１　質量・剛性パラメータによる２質点系モデル作成イメージ

まず、２個の質量とばねを持つ物理モデルを仮定し、１次と２次のモーダルパラメータから２自由度系の物理モデルを作成します。

なお、ここではモード質量を単位行列にするように正規化した固有モードを、正規モードと呼ぶことにします。

正規モードを用いれば、物理座標系の質量行列、剛性行列は次のよう表されます。

$$\Phi \Phi^T = \boldsymbol{M}^{-1} \tag{式-1}$$

$$\Phi ( \Omega^2 )^{-1} \Phi^T = \boldsymbol{K}^{-1} \tag{式-2}$$

ここで、質点の位置を３次モードの節である図１に示すＡ点とＢ点とし、モード解析により１次の振動モード形から求めたＡ点とＢ点の

１次の固有モード成分を$\Phi_{11}$、$\Phi_{21}$

同様に、

２次の固有モード成分を$\Phi_{12}$、$\Phi_{22}$

とすると、仮の固有モード行列は、次のようになります。

$$\Phi = \begin{bmatrix} \phi_{11} & \phi_{12} \\ \phi_{21} & \phi_{22} \end{bmatrix}$$

従って、(式-1)、(式-2)は次式のようになります。

$$\begin{bmatrix} {\phi_{11}}^2 + {\phi_{12}}^2 & \phi_{11} \phi_{21} + \phi_{12} \phi_{22} \\ \phi_{11} \phi_{21} + \phi_{12} \phi_{22} & {\phi_{21}}^2 + {\phi_{22}}^2 \end{bmatrix} = \begin{bmatrix} \frac{1}{M_1} & 0 \\ 0 & \frac{1}{M_2} \end{bmatrix} \tag{式-3} $$

$$\left[ \begin{array}{cc} \frac{{\phi_{11}}^2}{{\omega_1}^2} + \frac{{\phi_{12}}^2}{{\omega_2}^2} & \frac{\phi_{11} \phi_{21}}{{\omega_1}^2} + \frac{\phi_{12} \phi_{22}}{{\omega_2}^2} \\ \frac{\phi_{11} \phi_{21}}{{\omega_1}^2} + \frac{\phi_{12} \phi_{22}}{{\omega_2}^2} & \frac{{\phi_{21}}^2}{{\omega_1}^2} + \frac{{\phi_{22}}^2}{{\omega_2}^2} \end{array} \right]= \begin{bmatrix} \frac{1}{K_1} & \frac{1}{K_1} \\ \frac{1}{K_1} & \frac{1}{K_1} + \frac{1}{K_2} \end{bmatrix} \tag{式-4} $$

このとき、一般に(式-1)、(式-2)は成立しません。

これは、固有モード行列を分布定数系の振動モードから任意に抽出された固有モード成分から得ているため、(式-2)を満足し、(式-1)の右辺が対角行列となる固有モード行列を得られないため、集中定数系の条件を満足することができないためです。

そこで、これらの式を成立させ、２自由度系物理モデルに変換するためには、以下の拘束条件を満たす必要があります。

$$\phi_{11} \phi_{21} + \phi_{12} \phi_{22} = 0 \tag{式-5} $$

$$\left( \frac{\phi_{11} \phi_{21}}{{\omega_1}^2} + \frac{\phi_{12} \phi_{22}}{{\omega_2}^2} \right) \; – \; \left( \frac{{\phi_{21}}^2}{{\omega_1}^2} + \frac{{\phi_{22}}^2}{{\omega_2}^2} \right) = 0 \tag{式-6} $$

ここで、

(式-5)は、質量集中の条件を満たすための条件

(式-6)は、剛性行列の整合性を取るための条件

になります。

仮にこの拘束条件がなければ、ばねを２個とする仮定を満たさなくなります。
両式を物理モデルへの変換誤差と考え、次式の誤差関数$\varepsilon_1$、$\varepsilon_2$を定義します。

$$\varepsilon_1 = \phi_{11} \phi_{21} + \phi_{12} \phi_{22} \tag{式-7} $$

$$\varepsilon_2 = \frac{\phi_{11} \phi_{21} \; – \; {\phi_{21}}^2}{{\omega_1}^2} + \frac{\phi_{12} \phi_{22} \; – \; {\phi_{22}}^2} {{\omega_2}^2} \tag{式-8} $$

これらの誤差関数$\varepsilon_1$、$\varepsilon_2$を零（ゼロ）にするように固有モードを修正します。

そこで、固有モードに対する誤差関数の感度行列を次のように定めます。

$$\begin{bmatrix} \frac{\partial \varepsilon}{\partial \Phi} \end{bmatrix} = \begin{bmatrix} \frac{\partial \varepsilon_1}{\partial \Phi_{11}} & \frac{\partial \varepsilon_1}{\partial \Phi_{21}} & \frac{\partial \varepsilon_1}{\partial \Phi_{12}} & \frac{\partial \varepsilon_1}{\partial \Phi_{22}} \\ \frac{\partial \varepsilon_2}{\partial \Phi_{11}} & \frac{\partial \varepsilon_2}{\partial \Phi_{21}} & \frac{\partial \varepsilon_2}{\partial \Phi_{12}} & \frac{\partial \varepsilon_2}{\partial \Phi_{22}} \end{bmatrix} \tag{式-9} $$

ここで、$\Phi_{11}$、$\Phi_{21}$、$\Phi_{12}$、$\Phi_{22}$について、各々の修正量を$\delta{\Phi_{11}}$、$\delta{\Phi_{21}}$、$\delta{\Phi_{12}}$、$\delta{\Phi_{22}}$とします。

誤差関数を$\varepsilon_1$、$\varepsilon_2$を共に零とする固有モードの修正量を求めるには、以下の式を解けば良いことになります。

$$\begin{bmatrix} \frac{\partial \varepsilon} {\partial \Phi} \end{bmatrix} \begin{bmatrix} \delta \Phi_{11} & \delta \Phi_{21} & \delta \Phi_{12} & \delta \Phi_{22} \end{bmatrix}^T = \; – \; {\begin{bmatrix} \varepsilon_1 & \varepsilon_2 \end{bmatrix}}^T \tag{式-10} $$

つまり、次式で表される修正量を最小ノルム解を使った一般化逆行列により求め、誤差を零に収束させれば、(式-5)、(式-6)を満足する固有モードを得ることができます。

$$\begin{bmatrix} \delta \Phi_{11} & \delta \Phi_{21} & \delta \Phi_{12} & \delta \Phi_{22} \end{bmatrix}^T = \begin{bmatrix} \frac{\partial \varepsilon} {\partial \Phi} \end{bmatrix} {\left( \begin{bmatrix} \frac{\partial \varepsilon} {\partial \Phi} \end{bmatrix} {\begin{bmatrix} \frac{\partial \varepsilon} {\partial \Phi} \end{bmatrix}}^T \right)}^{-1} \left( \; – \; {\begin{bmatrix} \varepsilon_1 & \varepsilon_2 \end{bmatrix}}^T \right) \tag{式-11} $$

なお、誤差の収束範囲については、修正後の固有モードによるモード形と実際のモード形の形状や節の位置を比較し、ほぼ同一の形状となればよいと考えています。

ところで、ｉ次モードのｊ点における等価質量を$M_{eqij}$とすると、等価質量と固有モードの関係は次式となります。

$$M_{eqij} = \frac{1}{{\Phi_{ij}}^2} \tag{式-12} $$

従って、モード解析より求めた固有モードと、１自由度等価質量同定法により求めた各モードにおける最大振幅点での等価質量から、固有モード行列を求めることができます。

なお、正負については、伝達関数における位相を参照することにより決定しています。

平行板ばね構造物の２自由度系モデル作成例

下図に示す平行板ばね構造物を例にして、これまで述べてきた質量・剛性パラメータによる２質点系モデル作成法について説明します。

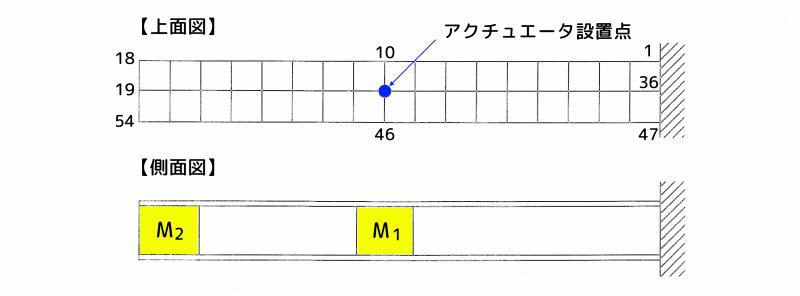
平行板ばね構造物

図２　平行板ばね構造物

平行板ばね構造物は、厚さ2mm、幅80mm、長さ720mmの鋼板２枚により、２個の鋼製ブロックを挟み込む平行板ばね構造となっています。

まず、実験モード解析により、制振対象である平行板ばね構造物の固有振動数と振動モード形を調べます。

下図に、実験モード解析により得た平行板ばね構造物の固有振動数と振動モード形、及び、２自由度系に低次元化した物理モデルを示します。

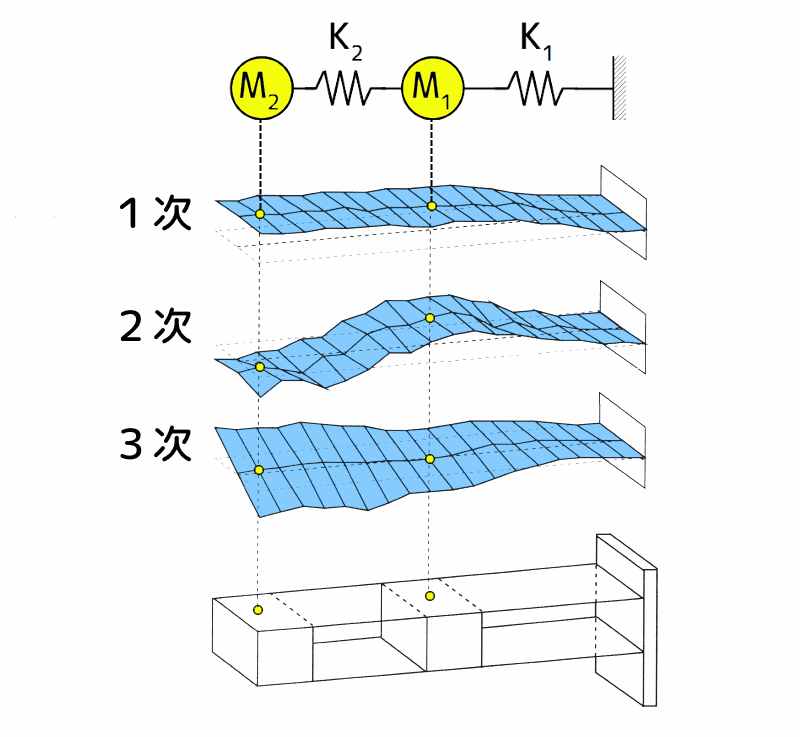
平行板ばね構造物の振動モード形と物理モデル

図３　平行板ばね構造物の振動モード形と物理モデル

実験モード解析の際の要素分割は、図２の【上面図】に示す通りです。

ここでは、制御対象モードを、１次と２次モードとします。

２自由度系モデルにより制御を行った場合、３次モードによるスピルオーバーの発生が懸念されます。

そこで、３次モードの節上にある上図の黄色〇印を質点の位置に決め、２自由度系物理モデルを作成します。

　参考：等価質量同定法について

(式-7)、(式-8)の誤差関数$\varepsilon_1$、$\varepsilon_2$を零にするように固有モードを修正した一例を以下に示します。

表　固有モード修正結果の一例

	修正前	修正後
固有モード行列	$$\Phi = \begin{bmatrix} 0.61 & 0.44 \\ 0.70 & 0.44 \end{bmatrix}$$	$$\Phi = \begin{bmatrix} 0.61 & 0.44 \\ 0.48 & 0.66 \end{bmatrix}$$
質量行列	$$\boldsymbol{M} = \begin{bmatrix} 2.05 & -0.69 \\ -0.69 & -1.71 \end{bmatrix}$$	$$\boldsymbol{M} = \begin{bmatrix} 1.77 & 0 \\ 0 & 1.51 \end{bmatrix}$$
剛性行列	$$\boldsymbol{K} = \begin{bmatrix} 32300 & -26100 \\ -26100 & 24600 \end{bmatrix}$$	$$\boldsymbol{K} = \begin{bmatrix} 15200 & -15200 \\ -15200 & 21800 \end{bmatrix}$$