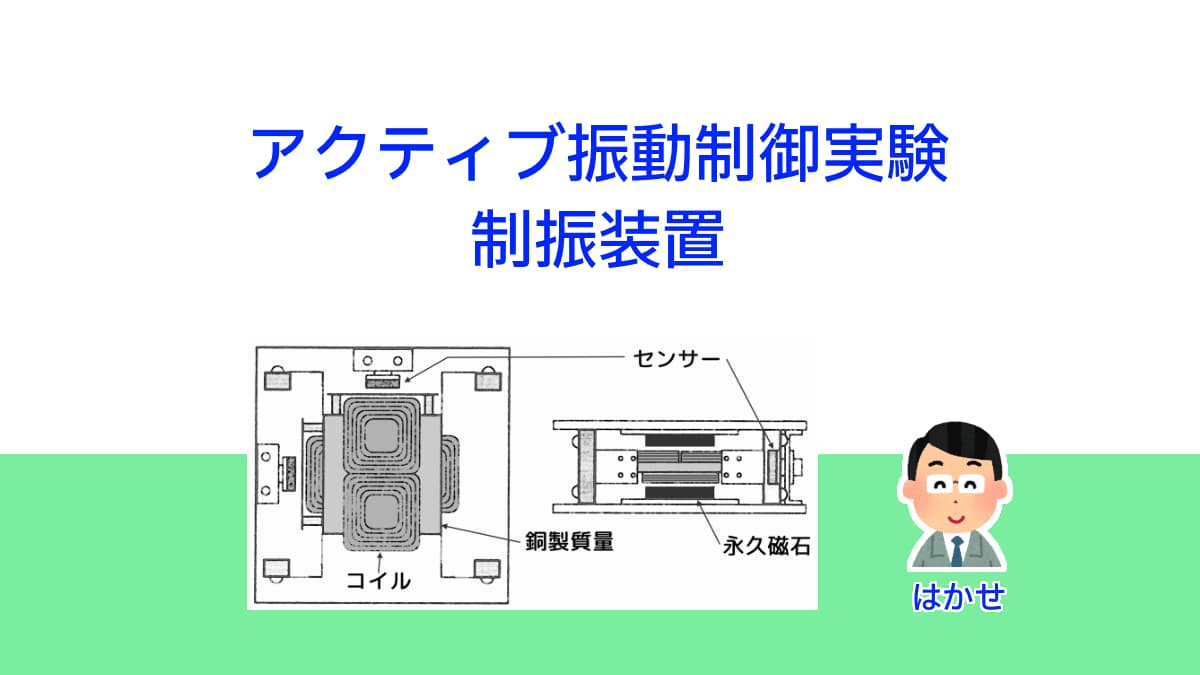
ここでは、アクティブ振動制御実験で使う制振装置を紹介します。
大学の研究室で振動制御実験をするときに使っていたものです。
学生向けの振動制御実験で使う場合には、いわゆる摩擦や減衰を考慮せずに使える制振装置の方がなにかと便利かと思います。
これは、振動制御では、モデリング、制御系設計、シミュレーション、実験とすべてやる必要があるからです。
まずは、研究室で学生の指導をする際に、振動制御とはどの様なものかを知り、少しづつ掘り下げていく進め方がよいと考えています。

研究室では、学生さん一人一人に合わせるようにはしていましたが、どこまでできていたかは分からないのですが。
ここで紹介している制振装置は、電磁力を利用しています。
電磁力については、以下のリンク先の「ガンプラのために学ぶ電気の法則」こちらを参照してください。

制振装置の分類
制振装置は、質量、ばね、ダンパの各要素からなり、パッシブ型、セミアクティブ型、アクティブ型、及び、ハイブリッド型の4通りに分類することができます。
慣性力利用方式の制振装置の分類を下図に示します。
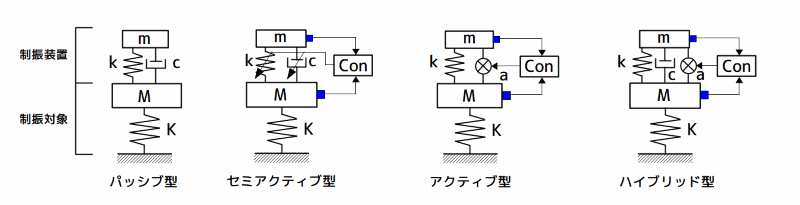
制振装置の分類
図1 制振装置の分類
これらの慣性力利用方式の基本的な考え方は、ある固有振動数を有する減衰のない制振対象に、質量・ばね・ダンパ要素からなる制振装置の固有振動数を同調し、さらに適当な減衰を付加することにより、制振対象に効果的な減衰を付与しようとするものです。
以下、4種類の慣性力利用方式の制振装置、パッシブ型、セミアクティブ型、アクティブ型、及び、ハイブリッド型について説明します。
パッシブ型(動吸振器)
パッシブ型は最適調整法が確立され、エネルギーを必要としない反面、制振対象のパラメータ変動により、その制振性能が左右されてしまいます。
このため、パラメータ変動に強い制振効果を必要とする場合には、アクティブ型の制振装置を使用する方が有利になります。
アクティブ型
アクティブ型は制振効果が高い反面、制御系に何らかのトラブルが生じた場合には、当然のことながら制振効果を得られないという問題があります。
また、アクティブ型は、その高い性能を機能を発揮するためには、常時エネルギーを必要とすることも課題となります。
このため、ハイブリッド型やセミアクティブ型の制振装置が使われることが多くなっています。
ハイブリッド型
ハイブリッド型は、パッシブ系とアクティブ系の制御系を含むため設計が複雑になるとういう面はあります。
しかし、アクティブ型と同等の制振性能を有し、かつ、制御系にトラブルが生じた場合にパッシブ型として機能するため信頼性の高い制振装置となります。
セミアクティブ型
セミアクティブ型は、制御力を加えるのではなく、制振装置の剛性(ばね)とダンパ(減衰)を調整することができる制振装置です。
アクティブ型やハイブリッド型ほど複雑な制御系を必要としない制振装置となります。
2次元ハイブリッド動吸振器
ここでは、2次元ハイブリッド動吸振器について説明します。
ハイブリッド動吸振器は、アクティブ動吸振器の持つ高い制振性能とパッシブ動吸振器の持つ高い信頼性を合わせ持ちます。
このため、何等かの理由によりアクティブ動吸振器の機能が停止した場合においても、パッシブ動吸振器の機能により安全性を確保する信頼性の高い構造と言えます。
また、塔状構造物の様に平面2方向で同様の振動特性を有する構造物には、X 軸とY軸の水平2方向の制御が可能な制振装置が必要となります。
下図に、水平2方向の振動制御に使える2次元ハイブリッド動吸振器の構造を示します。
左側の図が上方から、右側の図が側面から見た図です。
銅製のアクティブ質量(上図の黄緑色の部分)は、4個のL字型板ばねで支持されており、水平面内を自由に動けるようになっています。
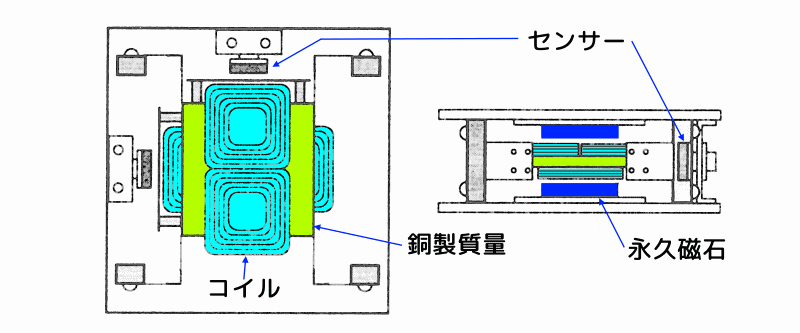
2次元ハイブリッド動吸振器の構造
図2 2次元ハイブリッド動吸振器の構造

機械的接触(摩擦)がない構造なので、シミュレーションと実験との比較がしやすいというメリットもあります。摩擦や減衰を考慮するとそれが研究テーマの1つになってしまいます。
アクティブ質量と構造物本体との相対変位は、X軸とY軸方向の2個の変位センサーより検出します。
アクティブ動吸振器としての機能
アクティブ動吸振器としての機能は、電磁力を利用しています。
アクティブ質量の両面に各々一対取り付けられたロ型の駆動コイルが、上下に置かれた永久磁石が作る磁場内で磁束を直角によぎる構造となっています。
アクティブ質量の上面と下面に設置したコイルに与える電流の向きを直交させることにより、アクティブ質量に電磁力による水平2方向の動きを与えることができます。
パッシブ動吸振器としての機能
パッシブ動吸振器としての機能は、磁気減衰力を利用しています。
アクティブ質量は、導体である銅で作られています。
アクティブ質量が上下の永久磁石により作られた磁場内で、磁束と直交して移動する時に渦電流が発生し、移動方向と逆向きの磁気減衰力が発生します。この磁気減衰力により、パッシブ動吸振器としての機能を実現しています。
この様に、アクティブ質量には磁気減衰力と電磁力が同時に作用する構造となっており、受動的動吸振器とアクティブ動吸振器の特性を兼ね備えたハイブリッド動吸振器を実現しています。
また、ここで紹介している2次元ハイブリッド動吸振器は、使用する永久磁石が一対で済み、1個のアクティブ質量で2方向の運動を制御することが可能なため軽量化と構造の簡素化を同時に実現しています。
アクティブ動吸振器
下図に、アクティブ動吸振器の構造を示します。
アクティブ動吸振器の構造
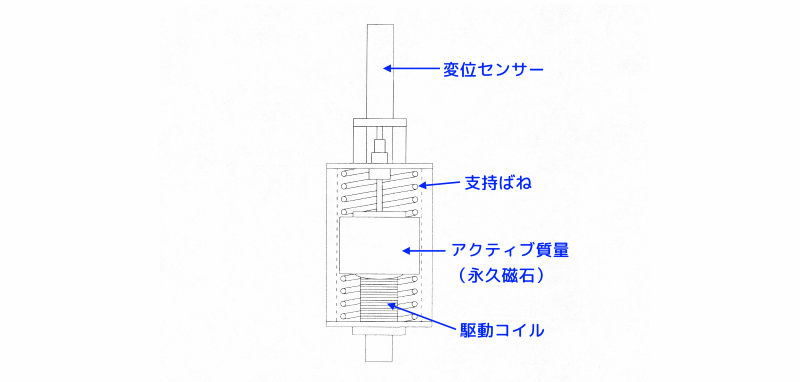
図3 アクティブ動吸振器の構造
このアクティブ動吸振器は、案内面支持による電磁力式リニアアクチュエータ方式です。
- リング状磁気回路を有するアクティブ質量を上下から支える支持ばねで支持しています。
- 変位センサーでは、本体とアクティブ質量間の相対変位を測定します。
考察:アクティブ動吸振器のヒステリシス特性
アクティブ動吸振器単体の特性を調べるため、アクティブ動吸振器を定盤に固定します。
制御力を加えこの時のアクティブマスの変位を動吸振器に設置されている変位センサーで検出します。
下図に、その測定結果の一例を示します。
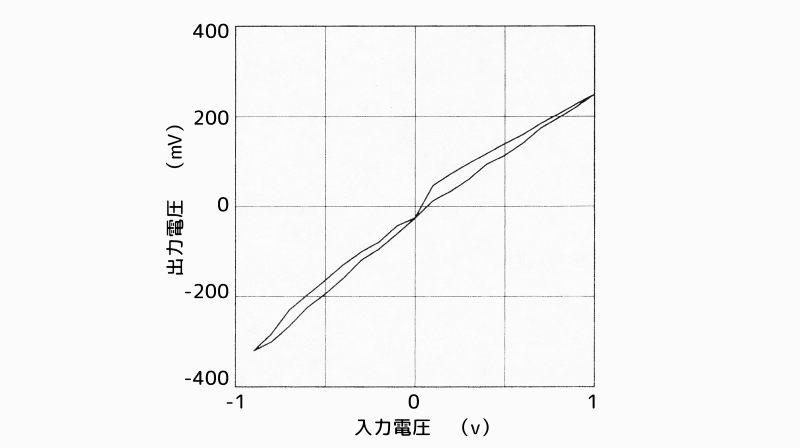
横軸にアクティブ動吸振器に加える入力電圧の値、縦軸に変位センサーの出力電圧を取り、入力電圧を連続的に変化させ、これに応じて出力される変位センサーの電圧をプロットしています。
アクティブ動吸振器の特性
図4 アクティブ動吸振器の特性
上図から、この動吸振器にはヒステリシス特性が存在することが分かります。
ヒステリシスの原因としては、次のように考えています。
アクティブマスを固定したシャフトは、ベアリングにより保持され、摩擦の影響を小さくする設計となっています。
しかし、シャフトとベアリングとの間に生じるわずかな摩擦の影響により、ヒステリシスが生じていると考えられます。
なお、ハイゲインの制御や精密な制御をする場合には、このヒステリシスが悪影響を与える恐れがあります。
この様な場合の対策としては、非線形成分であるヒステリシスを制御系設計において考慮する方法もありますが、重み係数行列によりヒステリシスの影響を緩和する方法があります。詳細は、以下のリンク先をご参照くだしさい。
3センサ式2次元ハイブリッド動吸振器
2次元ハイブリッド動吸振器は、X軸とY軸方向のアクティブ質量と構造物本体との相対変位の検出に、各軸1個計2個の変位センサーを使用しています。
この方法により測定された各軸の変位信号には、アクティブ質量のローリング成分が含まれています。
これまで紹介している振動制御例では、このローリング成分の影響を考慮しなくても特に問題とはなりませんでした。
振動モード形を利用したモデルによるタワー構造物のLQ最適制御入門
しかし、ハイ・ゲインにした場合や、より精度の高い制御を行なう場合においては、アクティブ質量のローリング成分によるスピルオーバ現象の発生が懸念されます。
そこで、以上の様な場合においてもスピルオーバーを防止できる、アクティブ質量のローリング成分を考慮したX・Y軸方向の変位を検出する方法について説明します。
この方法は、以下に示すように、3個の変位センサを使用することにより、容易に実現できます。
下図に、3個の変位センサを用いた場合の、センサとアクティブ質量との幾何学的関係を示します。

論文をまとめている頃、三角関数を使って数式を追いましたが、かなりてこずったことだけは覚えています。
頭の体操にいかがですか?
アクティブ質量と3個のセンサの幾何学的関係
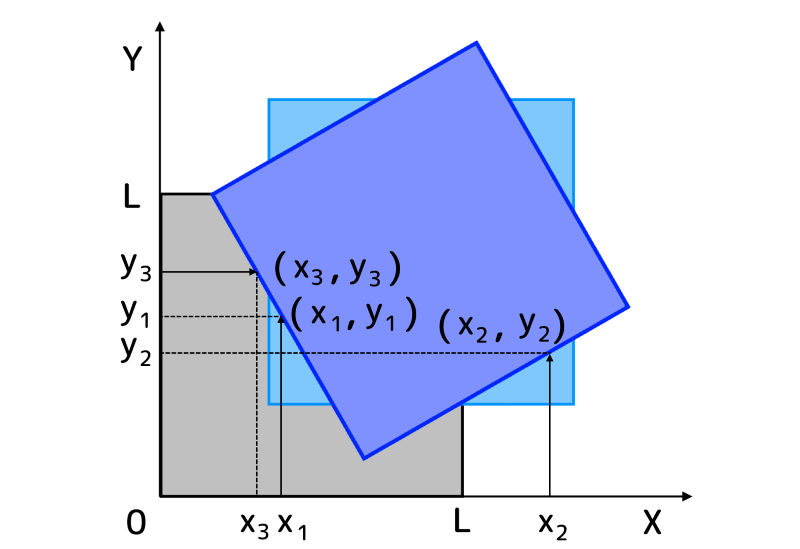
図5 アクティブ質量と3個のセンサの幾何学的関係
アクティブ質量は、1辺Lの正方形であり、変位センサは、X軸上に2個、Y軸上に1個の計3個設置します。
アクティブ質量が移動する前のそれぞれの変位計の座標を\( ( x_1 , 0 ) \)、\( ( x_2 , 0 ) \)、\( ( 0 , y_3 ) \)とし、それぞれの変位計が検出するアクティブ質量までの変位量を、\( y_1 \)、\( y_2 \)、\( x_3 \)とします。
また、もとのアクティブ質量の座標を\( ( x , y ) \)とし、X・Y方向にそれぞれ\( x_0 \)、\( y_0 \)移動し(上図水色の部分)、\( \theta \) 回転した時(上図青色の部分)のアクティブ質量の中心座標を\( ( x_r , y_r ) \)とすると、次の関係式が得られます。
$$ y \; – \; y_r = \tan \theta \; ( x \; – \; x_r ) \; – \; \frac{1}{2 \cos \theta}\tag{式-1}$$
$$ x \; – \; x_r = \; – \; \tan \theta \; ( y \; – \; y_r ) \; – \; \frac{1}{2 \cos \theta}\tag{式-2}$$
上式を整理すると、次式が得られます。
ここで、測定点の座標\( ( x_1 , y_1 ) \)、\( ( x_2 , y_2 ) \)、\( ( x_3 , y_3 ) \)を代入し、次式で整理すると、
$$ \Delta x = x_1 \; – \; x_2 $$
$$ \Delta y = y_1 \; – \; y_2 $$
次の関係式が得られます。
上式に含まれる変数は、全て既知、または、計測可能です。
したがって、ローリング成分を除去したアクティブ質量の変位を得ることができます。
これにより、ローリング成分によるスピルオーバーを防止すると共に、センサが2個の方式よりもさらに精密、あるいは、ハイ・ゲインの制御を実現することが可能となります。
動吸振器型ハイブリッド動吸振器
下図に、動吸振器型ハイブリッド動吸振器の構造を示します。
動吸振器型ハイブリッド動吸振器の構造
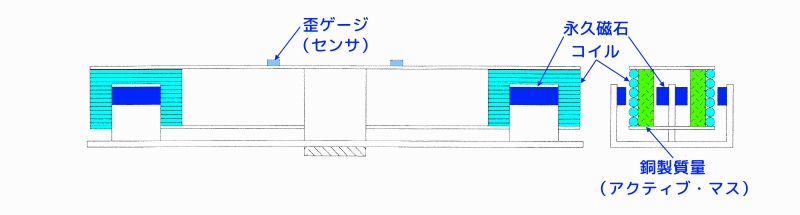
図6 動吸振器型ハイブリッド動吸振器の構造
上図のハイブリッド動吸振器は、二重動吸振器の銅製質量(アクティブ・マス)にコイルを巻いてハイブリッド・マスとしています。
すなわち、図中に示す2組の永久磁石とコイルにより発生する電磁力により、ハイブリッド・マスを駆動させています。
また、ハイブリッド・マスを導体である銅で作ることにより、これが磁場内で磁束と直交して運動(移動)する際に渦電流が発生し、運動と逆向きの磁気減衰力を得ることができる構造となっています。
従って、ハイブリッド・マスには磁気減衰力と電磁力が同時に作用します。
この構造によりパッシブ動吸振器とアクティブ動吸振器の特性を兼ね備えたハイブリッド動吸振器を実現しています。
このため、何等かの理由によりアクティブ動吸振器の機能が阻害された場合においても、パッシブ動吸振器としての機能が発揮され、安全性を確保する信頼性の高い構造となっています。
なお、ハイブリッド・マスの変位を測定するのに歪みゲージを使用しています。

歪ゲージを貼るのは一発勝負で、器用さも必要なため、研究室メンバー内で最適任者が選ばれていたように思います。
また、この制振装置は、水平方向だけでなく垂直方向の制振にも応用することが可能なため、様々な振動問題への応用が期待できます。
ハイブリッド動吸振器の信頼性と消費エネルギー
ここでは、ハイブリッド動吸振器とアクティブ動吸振器とを比較し、制振効果だけでなく、その信頼性と消費エネルギーについて考察します。
考察:ハイブリッド動吸振器の信頼性
ハイブリッド動吸振器とアクティブ動吸振器の信頼性につい て考察します。
下図に、速度項に重みを掛け、重み係数Rを変化させた場合の、ハイブリッド動吸振器設置点におけるアクティブ動吸振器とハイブリッド動吸振器の時間応答の比較を示します。
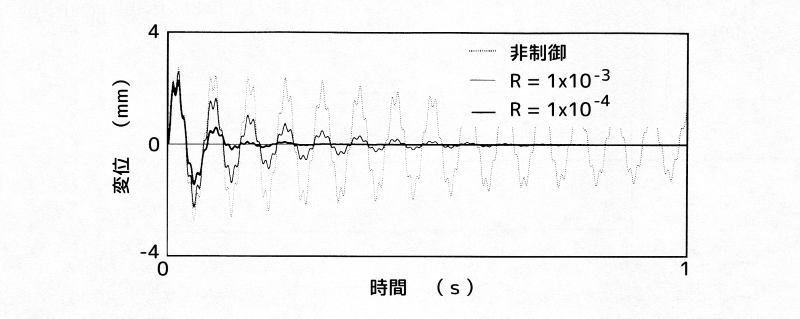
ハイブリッド動吸振器によるインパルス応答例
(a)ハイブリッド動吸振器によるインパルス応答例
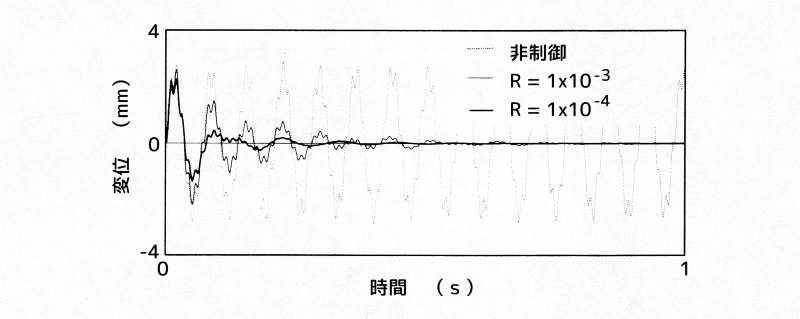
アクティブ動吸振器による制御例
(b)アクティブ動吸振器による制御例
図7 アクティブ動吸振器とハイブリッド動吸振器の比較
同図は、ハイブリッド動吸振器設置点をインパルス加振した時の時間応答です。シミュレーションの条件は次の通りです。
- 点線:非制御時
- 細線:制御時(速度項に重みを掛けた場合)
- \( \; Q = diag \begin{bmatrix} 1 & 1 & 0 & 0 & 0 & 0 \end{bmatrix} \)
- \(\ R = 1 \times 10^{-3} \)
- 太線:制御時(速度項に重みを掛けた場合)
- \( \; Q = diag \begin{bmatrix} 1 & 1 & 0 & 0 & 0 & 0 \end{bmatrix} \)
- \(\ R = 1 \times 10^{-4} \)
同図(a)の\(\ R = 1 \times 10^{-3} \)と\(\ R = 1 \times 10^{-4} \)の場合を比較します。
- 1個目のピークについては、その差がほとんどありません.
- 2個目以降のピークにおいては、振幅が\(\ R = 1 \times 10^{-3} \)の場合のおよそ半分になっています。
つまり、Rを小さくし制御量を大きくすることにより、より高い制振効果を得ることができます。
また、同図(b)においても同様の傾向を確認できます。
一方、同図(a)と(b)の非制御時の応答を比較すると、同図(a)においては,、ハイブリッド動吸振器のパッシブ動吸振器としての機能により、非制御時においても十分ではないがある程度の制振効果を維持しています。
しかし、同図(b)の非制御時は、不安定な応答を示しています。
この様に、ハイブリッド動吸振器は、アクティブ制御系の機能を失った 場合においても不安定とならない信頼性の高い設計であると言えます。
また、パッシブ系の制振効果は、ハイブリッド動吸振器のパッシブ系の最適設計により高めることができます。
考察:ハイブリッド動吸振器の消費エネルギー
ここでは、ハイブリッド動吸振器とアクティブ動吸振器の消費エネルギーについて考察します。
アクティブ動吸振器とハイブリッド動吸振器の制御エネルギー を、定量的に比較するため、評価式として以下に示す制御量と変位応答の2乗面積(ISE)を定義します。
$$\boldsymbol{J}_u = \int_0^\infty \boldsymbol{u}^2 \; dt \tag{式-1}$$
$$\boldsymbol{J}_x = \int_0^\infty \boldsymbol{x}^2 \; dt \tag{式-2}$$
\( \boldsymbol{J}_u \):制御量の2乗面積、消費エネルギーを示す。
\( \boldsymbol{J}_x \):変位応答の2乗面積、制振効果を示す。
速度に重みを掛け、制御量を左右する重み係数Rを変化させて、アクティブ動吸振器とハイブリッド動吸振器の\( \boldsymbol{J}_u \)と\( \boldsymbol{J}_x \)を比較した結果を下図に示します。
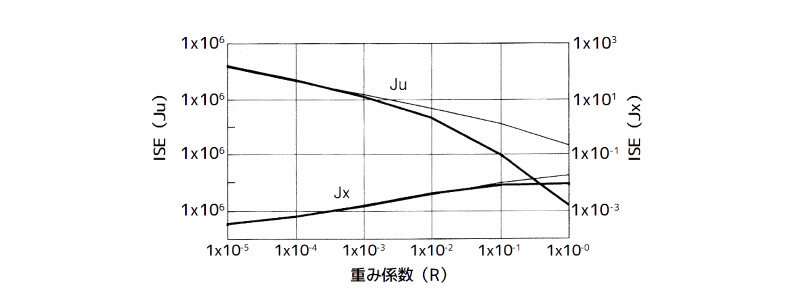
制振効果と消費エネルギ
図8 制振効果と消費エネルギ
同図の縦軸、横軸とも対数目盛です。
Rを小さくし制御を強く掛けると、\( \boldsymbol{J}_u \)の値が大きくなり、\( \boldsymbol{J}_x \)の値は小さくなります。
また、同図によれば、重み係数を\(\ R = 1 \times 10^{-3} \)より小さくした場合、すなわち制御を強く掛けた場合においては、ハイブリッド動吸振器とアクティブ動吸振器との消費エネルギーは同等となります。
一方、重み係数を\(\ R = 1 \times 10^{-3} \)より大きくした場合、すなわち、同図5-10(a)に示すような実用的と考えられる制御量を与える場合においては、ハイブリッド動吸振器のエネルギー消費の方がアクティブ動吸振器よりも小さく、ハイブリッド動吸振器が優れていると言えます。
以上、ハイブリッド動吸振器の信頼性と消費エネルギーについて考察し、アクティブ動吸振器に比べ、信頼性、及び、消費エネルギーの面からもハイブリッド動吸振器が優れていることをシミュレーションにより確認しました。
まとめ
ここでは、アクティブ振動制御の実験で使った制振装置について以下の項目で説明しました。
- 制振装置の分類
- 2次元ハイブリッド動吸振器(水平2方向の制振装置)
- アクティブ動吸振器
- 3センサ式2次元ハイブリッド動吸振器
- 動吸振器型ハイブリッド動吸振器
- ハイブリッド動吸振器の信頼性と消費エネルギー