ここでは、現代制御理論の1つであるLQ最適制御による制御系設計法について説明します。
「振動モード形を利用したモデルによるタワー構造物のLQ最適制御入門」では、
- 振動モード形を利用した塔状構造物のモデリング
- 現代制御理論(LQ最適制御)による制御系設計
- ハイブリッド動吸振器による実験
により、塔状構造物の振動制御(制振)方法の全体像について紹介しています。
また、モデリングについては、「振動モード形を利用したモデリング入門」で説明しています。
アクティブ制振のための制御理論について
制御理論は、
- 古典制御理論
- 現代制御理論
とに分けられます。
古い制御理論だから使えないとか、新しい理論だから優れているわけではありません。
実際のところ、古典制御理論にも、現代制御理論にもそれぞれメリットや課題があり、制御の目的に応じて使い分けているのが現状です。
古典制御理論のメリットと課題
古典制御理論は、1950年代にほぼ完成され、PID制御は今でも実用性の高い設計法として使われています。
PID制御(Proportional-Integral-Differential Controller)は、次のPIDという3つの要素を使った制御のことです。
- 比例(Proportional)
- 積分(Integral)
- 微分(Differential)
これらの3つの要素を調整することで、1入力1出力の制御系を設計することができ、現在でも産業界では主力の制御系だと言われています。
しかし、その反面、
- 経験的要素が多い。
- 周波数領域におけるスカラ系を対象とするため多変数系への拡張が困難で効果的な減衰を付与することが簡単な問題ではない。
などの課題があります。
一方、最適制御理論に代表される現代制御理論は、1960年代にKalmanらにより大系化されましたが、出現当初は難解なため実用性が疑問視されていました。
しかし、2000年代のコンピュータの演算能力の高性能化やDSPなどの登場にみられるハードウェアの進歩と、制御系設計用ツール等のソフトウェアの充実により、現在では容易に利用可能となり、アクティブ制振装置と共に振動制御の分野でも幅広く活用されています。
現代制御理論のメリットと課題
現代制御理論は、システムを状態方程式で表現した後に、望ましい評価関数を最小にする意味での最適制御という概念に基づき、理論的に制御系を設計するため、多変数系を理論的に扱うことができます。
現代制御理論には、多入力・多出力の制御系を扱えるメリットがある反面課題もあります。
例えば、現代制御理論の1つであるLQ制御理論は、線形2次形式の評価関数を最小にすることにより、制御性能及び制御入力の設計要求を同時に満足させるフィードバックゲインを決定することができます。
しかし、設計パラメータである重み係数と制振効果との関係が明らかでないため、試行錯誤的に重み係数を決定しているのが現状です。
そこで、根軌跡図を活用することにより、所望の制振効果を得られる重み係数(行列)の決め方を紹介します。
また、最適制御理論は、システムを状態方程式で表現した後に、理論的に制御系を設計するため、良好な制御系を設計するためには、良好な振動系のモ デリングが必須です。
ここでは、「振動モード形を利用したモデリング入門」により作成した低次元化モデルを用いて、現代制御理論により制御系を設計する方法について説明します。
主な項目は次の通りです。
- 運動方程式を状態方程式表示
- 状態方程式と可制御・可観測性との関係
- LQ制御理論
- 制御系設計例
- アクティブ動吸振器による2自由度系の制御系設計法について説明します。
- ここで説明している振動制御法の有効性を、シミュレーションと実験により確認します。
運動方程式と振動制御系
一般に、アクティブ制振装置を含むN自由度系の運動方程式は、次式で表されます。
$$\boldsymbol{M} \ddot{\boldsymbol{x}} + \boldsymbol{C} \dot{\boldsymbol{x}} + \boldsymbol{K} \boldsymbol{x} = \boldsymbol{K} \boldsymbol{u} + \boldsymbol{K}_d \boldsymbol{w} \tag{式-1}$$
ただし、
\(\boldsymbol{x}\):変位ベクトル
\(\boldsymbol{M}\):質量行列
\(\boldsymbol{C}\):減衰行列
\(\boldsymbol{K}\):剛性行列
\(\boldsymbol{u}\):制御量ベクトル
\(\boldsymbol{w}\):外力ベクトル
\(\boldsymbol{K}\):制御力係数ベクトル
\(\boldsymbol{K}_d\):外乱力係数ベクトル
\(i\)、\(j\):制御力及び外乱力の個数
ここで、状態変数ベクトルを次のように定義します。
$$\boldsymbol{X} = \begin{Bmatrix}{\dot{x} \\ x} \end{Bmatrix} \tag{式-2}$$
この状態変数ベクトルを用いると、制振対象の状態方程式は次式となります。
$$\dot{\boldsymbol{X}} = \boldsymbol{A} \boldsymbol{X} + \boldsymbol{b} \boldsymbol{u} + \boldsymbol{E} \boldsymbol{w} \tag{式-3}$$
ただし、
$$\boldsymbol{A} = \begin{bmatrix} – \boldsymbol{M}^{-1} \boldsymbol{C} & – \boldsymbol{M}^{-1} \boldsymbol{K} \\ \boldsymbol{I}_{N,N} & \boldsymbol{0}_{N,N} \end{bmatrix}$$
$$\boldsymbol{B} = \begin{Bmatrix} \boldsymbol{M}^{-1} \boldsymbol{K}_f \\ \boldsymbol{0}_{1,N} \end{Bmatrix}$$
$$\boldsymbol{E} = \begin{Bmatrix} \boldsymbol{M}^{-1} \boldsymbol{K}_d \\ \boldsymbol{0}_{1,N} \end{Bmatrix}$$
\(\boldsymbol{0}_{i,j}\):i行j列の零行列
\(\boldsymbol{I}_{i,j}\):i行j列の単位行列
状態変数ベクトルは、2x1の要素よりなりますが、実際に観測する状態変数の数をp個とすれば、観測ベクトルは次式で表されます。
$$\boldsymbol{y} = \boldsymbol{C} \boldsymbol{X} \tag{式-4}$$
ただし、
\(\boldsymbol{C}\):px2の観測行列
ここで、次式の様な状態フィードバックを行うことにします。
$$\boldsymbol{u} = – \boldsymbol{K}_g \boldsymbol{X} \tag{式-5}$$
ただし、
\(\boldsymbol{K}_g\):jx2のフィードバックゲイン行列
この状態フィードバックゲインをLQ制御理論により求めることで、漸近安定の保証された制御系を構成することができます。
状態方程式と可制御性・可観測性
LQ制御理論は、システムの可制御性と可観測性が保証された場合に適用することができます。
ここでは、システムの可制御・可観測性について説明します。
次式で表される線形システムを仮定します。
$$\dot{\boldsymbol{X}} = \boldsymbol{A} \boldsymbol{X} + \boldsymbol{b} \boldsymbol{u} \tag{式-6}$$
$$\boldsymbol{y} = \boldsymbol{C} \boldsymbol{X} \tag{式-7}$$
可制御である条件は、次式で表される可制御行列\(\boldsymbol{U}_c\)の階数 (rank)がnであることです。
すなわち、
$$\boldsymbol{U}_c = \begin{bmatrix} \boldsymbol{b}, \boldsymbol{A}\boldsymbol{b}, \boldsymbol{A}^2 \boldsymbol{b}, \ldots , \boldsymbol{A}^{N-1} \boldsymbol{b} \end{bmatrix} \tag{式-8}$$
の時、
$$rank \; \boldsymbol{U}_c = n \tag{式-9}$$
であれば可制御となります。
可観測である条件は、次式で表される可制御行列\(\boldsymbol{U}_o\)の階数(rank)がnであることです。
すなわち、
の時、
$$rank \; \boldsymbol{U}_o = n \tag{式-11}$$
であれば可観測となります。
LQ制御理論
LQ制御理論により制御系を設計する場合、設計パラメータは、次式の2 次形式評価関数\(\boldsymbol{J}\)に与える重み係数行列\(\boldsymbol{Q}\)と重み係数行列\(\boldsymbol{R}\)になります。
$$\boldsymbol{J} = \int_0^\infty ( \boldsymbol{X}^T \boldsymbol{Q} \boldsymbol{X} + \boldsymbol{u}^2 \boldsymbol{R} ) \; dt \tag{式-12}$$
ここで、評価関数を次式のように表します。
$$\boldsymbol{J} = \boldsymbol{J}_x + \boldsymbol{J}_u \tag{式-13}$$
ただし、
$$\boldsymbol{J}_x = \int_0^\infty \boldsymbol{X}^T \boldsymbol{Q} \boldsymbol{X} \; dt$$
$$\boldsymbol{J}_u = \int_0^\infty \boldsymbol{u}^2 \boldsymbol{R} \; dt$$
ここで、\(\boldsymbol{J}_x\)は状態変数の2乗積分誤差であり、制御性能を表しています。
一方、\(\boldsymbol{J}_u\)は入力変数の2乗積分値となっており、制御に必要とされるエネルギを表しています。
\(\boldsymbol{J}_u\)と\(\boldsymbol{J}_u\)を同時に小さくできるのであれば、それが良い制御系と言うことができます。
しかし、\(\boldsymbol{J}_u\)と\(\boldsymbol{J}_u\)に要求されている内容は、相反するものであり、実際には設計パラメータである重み係数行列\(\boldsymbol{Q}\)と重み係数行列\(\boldsymbol{R}\)により、両者のトレードオフを図る(バランスを取る)ことが必要となります。
LQ制御理論によれば、この評価関数\(\boldsymbol{J}\)を最小にする制御量\(\boldsymbol{u}\)は、次のように定式化されています。
$$\boldsymbol{u} = \; – \boldsymbol{R}^{-1} \boldsymbol{b}^T \boldsymbol{P} \boldsymbol{X} = \; – \boldsymbol{K} _g \boldsymbol{X} \tag{式-14}$$
ただし、\(\boldsymbol{P}\)は、次式のリカッチ方程式の解です。
このリカッチ方程式を解くことにより、状態フィードバックゲインを求めることができます。
(式-3)に(式-14)を代入した次式で表される閉ループシステムは、最適レギュレータと呼ばれています。
$$\dot{\boldsymbol{X}} = ( \boldsymbol{A} \; – \boldsymbol{B} \boldsymbol{K}_g ) \boldsymbol{X} + \boldsymbol{E} \boldsymbol{w} \tag{式-16}$$
最適レギュレータは漸近安定、つまり、次式の行列は安定行列となり、その固有値も自動的に決定されます。
$$\boldsymbol{A}^0 = \boldsymbol{A} \; – \boldsymbol{B} \boldsymbol{K}_g \tag{式-17}$$
アクティブ動吸振器による平行板バネ構造物の制御系設計
制振対象は平行板ばね構造物とし、「振動モード形を利用したモデリング入門」によりモデルを作成し、アクティブ動吸振器により、制振対象の1次と2次の振動モードを制御します。
制御力の調整(制振効果をどの程度にするか)については、根軌跡図を利用した制御系設計法を説明します。
制御対象の運動方程式と状態方程式
下図に、制振対象とアクティブ動吸振器を含めた力学モデルを示します。
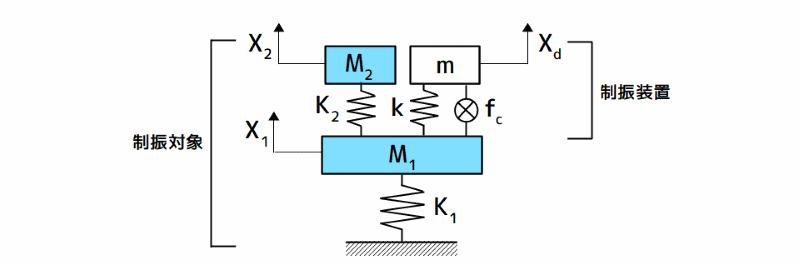
制振対象とアクティブ動吸振器の力学モデル
図1 制振対象とアクティブ動吸振器の力学モデル
ここで、相対変位を次のように定義します。
$$\boldsymbol{X}_c = \boldsymbol{X}_d \; – \boldsymbol{X}_1 \tag{式-18}$$
この相対変位を用いると上図の力学モデルの運動方程式は、以下のようになります。
$$\ddot{\boldsymbol{X}_2} = \frac{\boldsymbol{K}_2}{\boldsymbol{M}_2} \boldsymbol{X}_1 \; – \frac{\boldsymbol{K}_2}{\boldsymbol{M}_2} \boldsymbol{X}_2 \tag{式-20}$$
状態変数ベクトルを次のように定義すると、
$$\boldsymbol{X} = \begin{Bmatrix} \; \dot{X_1} \; \dot{X_2} \; \dot{X_c} \; X_1 \; X_2 \; X_c \end{Bmatrix}^T \tag{式-22}$$
状態方程式は、次式で表されます。
$$\dot{\boldsymbol{X}} = \boldsymbol{A} \boldsymbol{X} + \boldsymbol{b} \boldsymbol{u} \tag{式-23}$$
ただし、
$$\boldsymbol{b} = K_c \cdotp \begin{bmatrix} \frac{1}{M_1} & 0 & – \left( \frac{1}{M_1} + \frac{1}{m} \right) & 0 & 0 & 0 \end{bmatrix}^T$$
\(K_c\):制御力と制御量との関係を示す力変換係数
LQ制御理論による制御系設計
制御系設計には、上述のLQ制御理論を用います。
ここでの設計パラメータは、次式で表される線形2次形式の評価関数\(\boldsymbol{J}\)に与える重み係数行列\(\boldsymbol{Q}\)と重み係数\(R\)になります。
$$\boldsymbol{J} = \int_0^\infty ( \boldsymbol{X}^T \boldsymbol{Q} \boldsymbol{X} + u^2 R ) \; dt \tag{式-24}$$
ただし、
$$\boldsymbol{Q} = diag \; \left[ \; q_1, q_2, q_3, q_4, q_5, q_6 \right]$$
ここで、
\(q_1\):質点1の速度に掛かる重み係数
\(q_2\):質点2の速度に掛かる重み係数
\(q_3\):相対速度に掛かる重み係数
\(q_4\):質点1の変位に掛かる重み係数
\(q_5\):質点1の変位に掛かる重み係数
\(q_6\):相対変位に掛かる重み係数
LQ制御理論によれば、この評価関数\(\boldsymbol{J}\)を最小にする制御量\(u\)は、次のように定式化されています。
$$u = \; – R^{-1} \boldsymbol{b}^T \boldsymbol{P} \boldsymbol{X} = \; – \boldsymbol{K} _g \boldsymbol{X} \tag{式-25}$$
ただし、
$$\boldsymbol{K} = \begin{Bmatrix} k_1, k_2, k_3, k_4, k_5, k_6 \end{Bmatrix} $$
ここに、\(\boldsymbol{P}\)は、次式のリカッチ方程式の解です。
このリカッチ方程式を解くことにより、状態フィードバックゲインを求めることができます。
ところが、設計パラメータである重み係数行列\(\boldsymbol{Q}\)と重み係数\(R\)の値と得られる制御系の特性との関係が不明であるため、試行錯誤的に設計パラメータを決定し、制御系を設計しているのが現状です。
そこで、無次元化状態方程式を用い、無次元系の重み行列を定義することで、解析結果に一般性を持たせることができますが、これについては別途に紹介します。
制振効果の解析
重み係数による制振効果の違いについて、根軌跡図、周波数応答(伝達関数)、及び、シミュレーション(インパルス応答、時間応答)により確認します。
根軌跡図による重み係数による制振効果の比較

ここでは、無次元系の根軌跡図を使っています。無次元系の状態方程式と根軌跡図による制振効果については、後日説明する予定です。
無次元系の重み係数行列\(\boldsymbol{Q}\)と重み係数\(R\)の値と得られる制御系の特性との関係を明らかにするため、根軌跡図を利用します。
図2は質点1と質点2の変位項に、図3は質点1と質点2の速度項に重みを掛け、重み係数\(R\)を小さくした(制御を強くしていった)場合の無次元系の根軌跡図です。
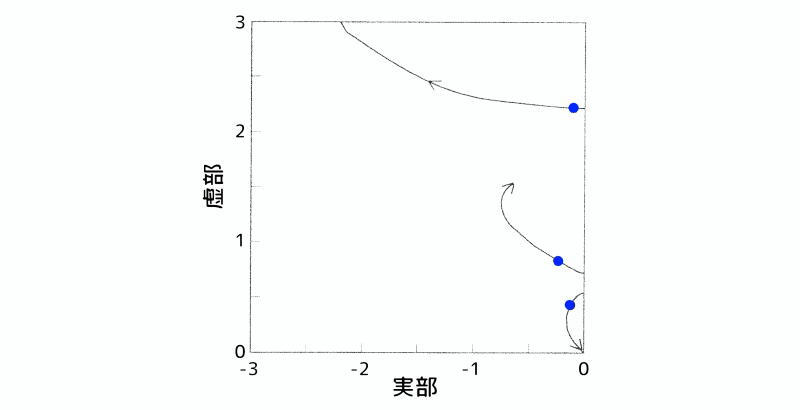
根軌跡図:質点1と質点2の変位項に重みを掛けた場合
図2 根軌跡図:質点1と質点2の変位項に重みを掛けた場合
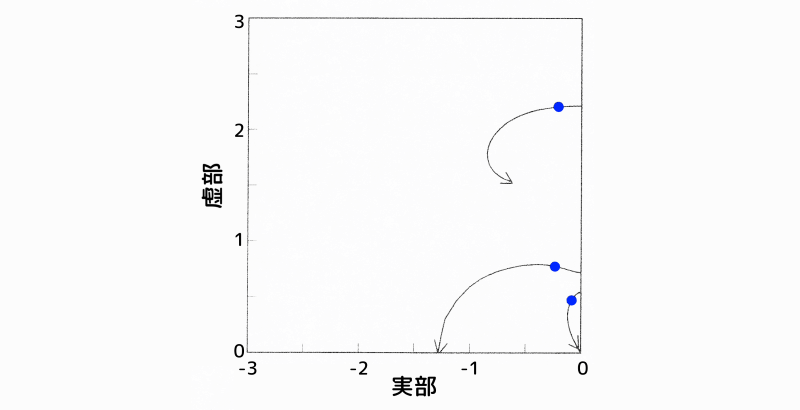
根軌跡図:質点1と質点2の速度項に重みを掛けた場合
図3 根軌跡図:質点1と質点2の速度項に重みを掛けた場合
この系においては、3個の特性根が存在します。原点に近い根から、アクティブ動吸振器、制振対象の1次、2次の根になります。
また、根軌跡図において、根と実軸とがなす角度は減衰の程度を示しています。つまり、根が実軸から離れるほど制振効果が高くなるということです。
なお、変位項と速度項の制振効果の比較のため、根軌跡図に\(R=10\)の点を青丸でプロットしています。
図2、図3から、以下の事が分かります。
(1)変位項に重みを掛けた場合
- アクティブ動吸振器の根と制振対象の1次の根は互いに反発し、アクティブ動吸振器の根は原点に収束します。
- 制振対象の1次と2次の根は、当初接近しますが、その後1次の根はS平面の1点に収束し、2次の根はさらにS平面を左に移動します。
(2)速度項に重みを掛けた場合
- アクティブ動吸振器の根は、原点に収束します。
- 制振対象の1次と2次の根は、当初接近しますが、1次の根は実軸上に引き込まれ、2次の根はS平面の1点に収束します。
(3)制振効果の比較
図2、図3の青丸は、それぞれ変位項、速度項に重みを掛け、重み係数を\(R=10\)とした場合の根で、次のことが分かります。
- アクティブ動吸振器の根と制振対象の1次の根は、虚軸からほとんど同一の点にあります。
- 制振対象の2次の根は、速度項に重みを掛けた場合の方が虚軸より左に位置しています。
従って、速度項の方が、変位項よりも2次のピークをより大きく安定化する効果があると考えることができます。
伝達関数による重み係数による制振効果の比較
変位項と速度項の制振効果を周波数応答(伝達関数)により比較します。
図4に、重み係数による周波数応答の比較を示します。
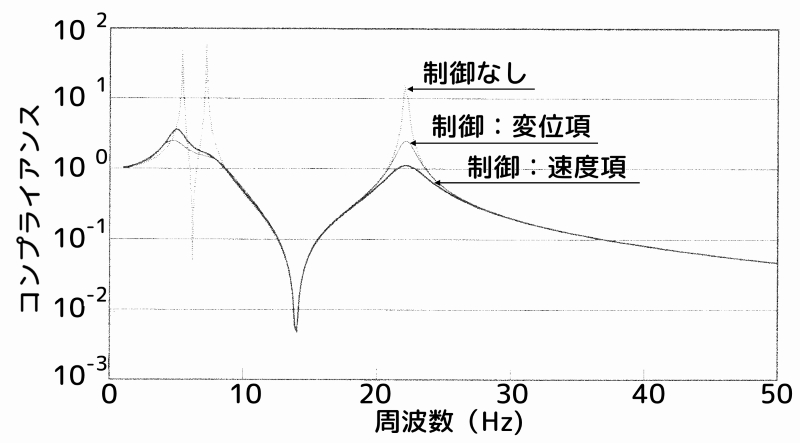
重み係数による周波数応答の比較
図4 重み係数による周波数応答の比較
上図において、点線が非制御時、細線が変位項に重みを掛けた場合、太線が速度項に重みを掛けた場合の周波数応答(伝達関数)です。
同図より、根軌跡図での解析と同様、速度項に重みを掛けた場合のほうが、2次モードの安定化効果が高いことが分かります。
これまでの結果から、2次のピークを安定化させたい場合には、速度項に重みを掛けた方が、変位項に重みを掛けた場合よりも制振効果が高いことが分かります。
この様に、重み係数に応じた根軌跡図を作成することにより、重み係数と得られる制御系の特性との関係を明らかにすることができます。
シミュレーション(インパルス応答)による重み係数による制振効果の比較
下図に、変位項に重みを掛けた場合のインパルス応答(時間応答)を示します。
上図の上側が質点1、下側が質点2のインパルス応答です。
細線が非制御時、太線が制御時の応答です。
制御により、速やかに振動が収束していることが分かります。
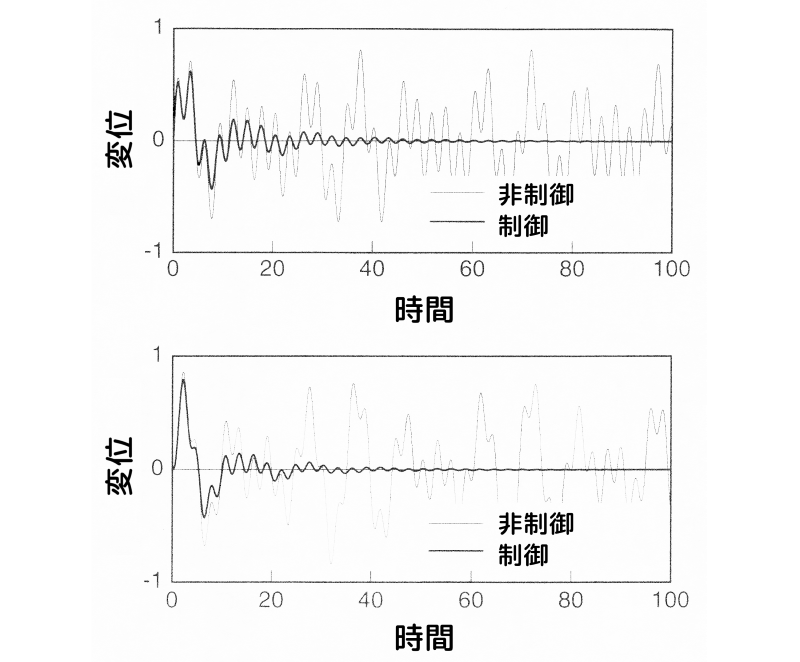
変位項に重みを掛けた場合のインパルス応答
図5 変位項に重みを掛けた場合のインパルス応答
下図に、速度項に重みを掛けた場合の時間応答(インパルス応答)を示します。
上図の上側が質点1、下側が質点2のインパルス応答です。
細線が非制御時、太線が制御時の応答です。
制御により、速やかに振動が収束していることが分かります。
また、図5の変位項に重みを掛けた場合と比べると、速度項に重みを掛けた場合の方が、2次の振動がより早く収束していることが分かります。
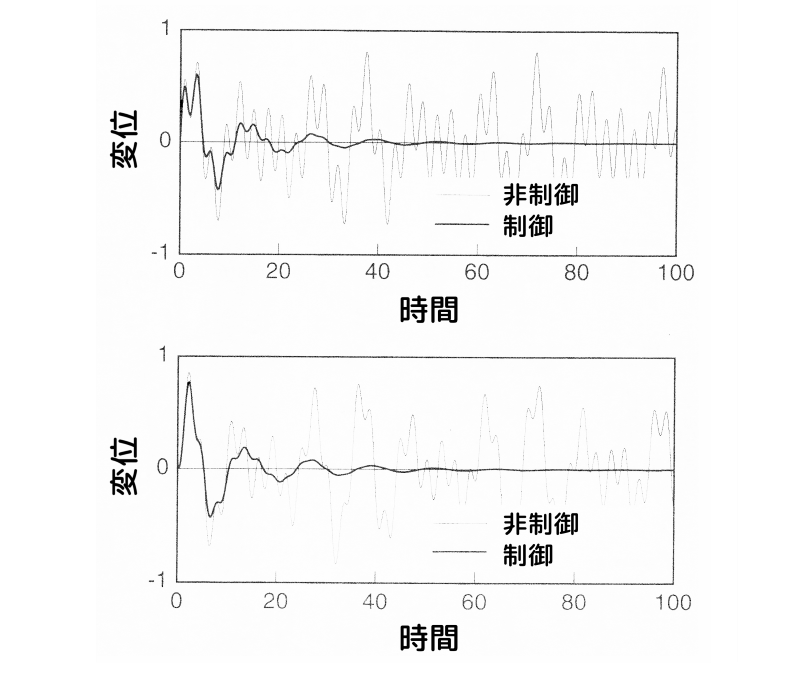
速度項に重みを掛けた場合のインパルス応答
図6 速度項に重みを掛けた場合のインパルス応答
振動制御実験による制振効果の確認
実験装置と実験方法
下図に、実験装置の構成を示します。
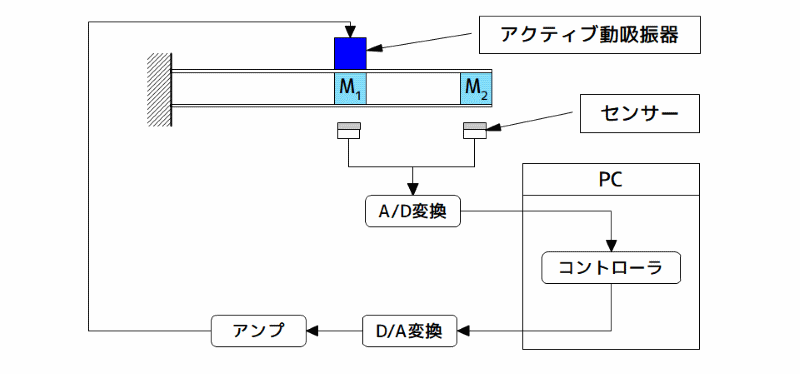
実験装置の構成
図7 実験装置の構成
実験装置の構成品は、以下の通りです。
- 質点1、質点2の絶対変位を検出するための2個の変位センサー
- アクティブ動吸振器(変位センサーを含む)
- コントローラーであるパソコン
- A/D・D/A変換ボード(パソコンに内蔵)
- 制御信号を増幅してアクティブ動吸振器を駆動するためのアンプ
変位センサーで得られた変位信号(アナログ信号)は、A/D変換ボードを介してパソコンに入力されます。速度振動は、差分により作り、6個の状態量を得ています。
これらの状態量に、重み係数により決定されたフィードバックゲインを乗じて制御量を算出し、状態フィードバックを実現しています。
実験は、制御を掛けた状態で、制振対象の先端をインパルス加振し、この時の時間応答を評価します。
なお、重み係数\(R\)については、当初大きい値を使用し、徐々に値を小さくして制御を強く掛けています。
下図に、アクティブ動吸振器の構造を示します。
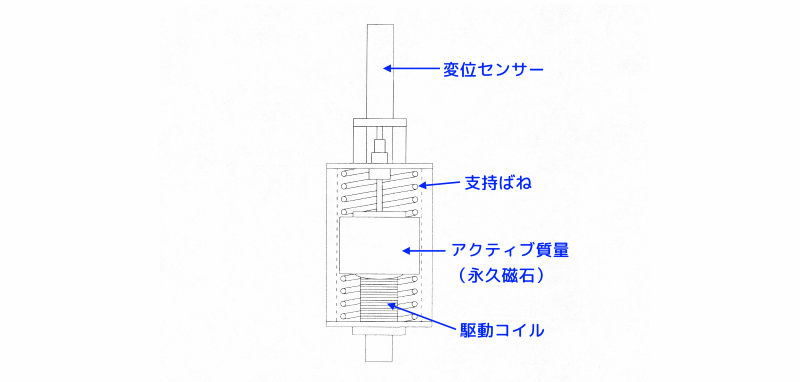
アクティブ動吸振器の構造
図8 アクティブ動吸振器の構造
このアクティブ動吸振器は、案内面支持による電磁力式リニアアクチュエータ方式です。
- リング状磁気回路を有するアクティブ質量を上下から支える支持ばねで支持しています。
- 変位センサーでは、本体とアクティブ質量間の相対変位を測定します。
実験:重み係数による制振効果の比較
重み係数による制振効果の違いを確認するため、変位項に重みを掛けた場合と速度項に重みを掛けた場合のインパルス応答(時間応答)を比較します。
図9、図10に、それぞれ変位項、速度項に重みを掛けた場合のインパルス応答(時間応答)の実験結果を示します。
両図において、上側が質点1、下側が質点2のインパルス応答です。
細線が非制御時、太線が制御時の応答です。
両図より、制御により速やかに振動が収束していることが分かります。
なお、非制御時にも振動が収束している理由については、次項で考察します。
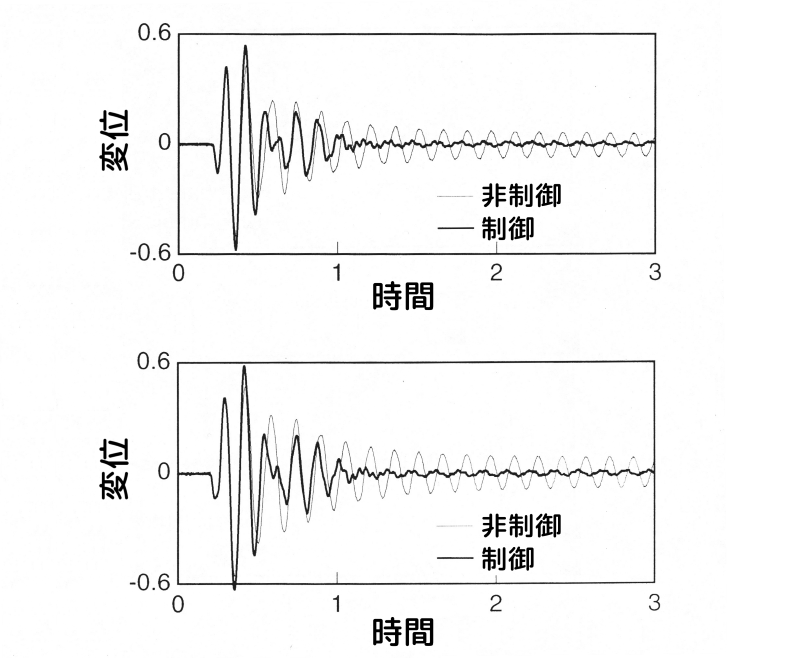
変位項に重みを掛けた場合のインパルス応答
図9 変位項に重みを掛けた場合のインパルス応答
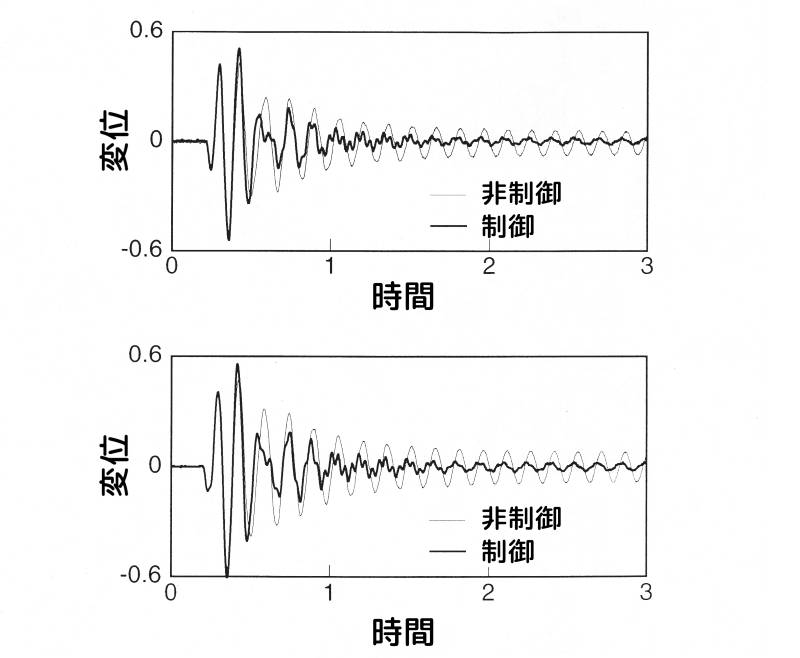
速度項に重みを掛けた場合のインパルス応答
図10 速度項に重みを掛けた場合のインパルス応答
考察:重み係数による制振効果の改善
図9、図10から、制御により速やかに振動が収束していることを確認できますが、非制御時の時間応答が収束傾向にあります。
これは、アクティブ動吸振器内の摩擦による影響であると考えられます。
また、速度項に重みを掛けた場合に、シミュレーション結果の様に、2次の振動が十分に抑制されていません。
これは、使用したアクティブ動吸振器固有のヒステリシス特性のため、重み係数\(R\)を十分に小さくできなかった(十分な制御を掛けられなかった)ため、結果として2次の振動を十分に抑制できなかったと考えられます。
この対策としては、制御系にアクティブ動吸振器のヒステリシス特性を含めることが考えられますが、ここでは、重み係数の設定によりアクティブ動吸振器のヒステリシスの影響を小さくする方法を説明します。
これまで、アクティブ動吸振器の制振効果を最大限に発揮させるため、重み係数行列\(\boldsymbol{Q}\)のアクティブ質量の相対変位と相対速度の重みを零(ゼロ)としていました。
そこで、アクティブ質量の項に重みを掛けることにより、アクティブ質量の挙動を抑制するようなフィードバックゲインを使い、ヒステリシ スの影響を緩和し、重み係数\(R\)を小さくして制振効果を高めることにします。
この効果を確認するため、インパルス加振実験を行いました。
下図に、この時の時間応答の実験結果を示します。
相対速度に重みを掛けることにより、重み係数\(R\)を十分小さくすることが可能となり、2次の振動も十分に抑制された良好な制振効果を得ることができます。
この様に、アクティブ動吸振器のヒステリシス特性のような非線形性を、重み係数により改善することが可能であることを実験により確認しました。
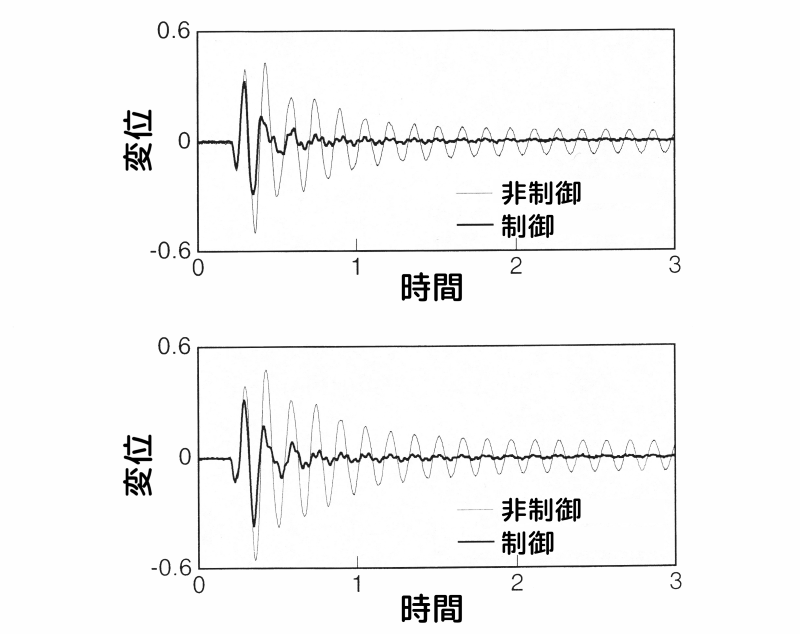
相対速度を含めた速度項に重みを掛けた場合のインパルス応答
図11 相対速度を含めた速度項に重みを掛けた場合のインパルス応答
まとめ
ここでは、LQ最適制御によるアクティブ制振の制御系設計法について、説明しました。
主な項目は、次の通りです。
- アクティブ制振のための制御理論
- 運動方程式と振動制御
- 状態方程式と可制御性・可観測性
- LQ制御理論
- 制振効果の解析
- 根軌跡図、伝達関数、インパルス応答による重み係数による制振効果の比較
- 振動制御実験による制振効果の確認