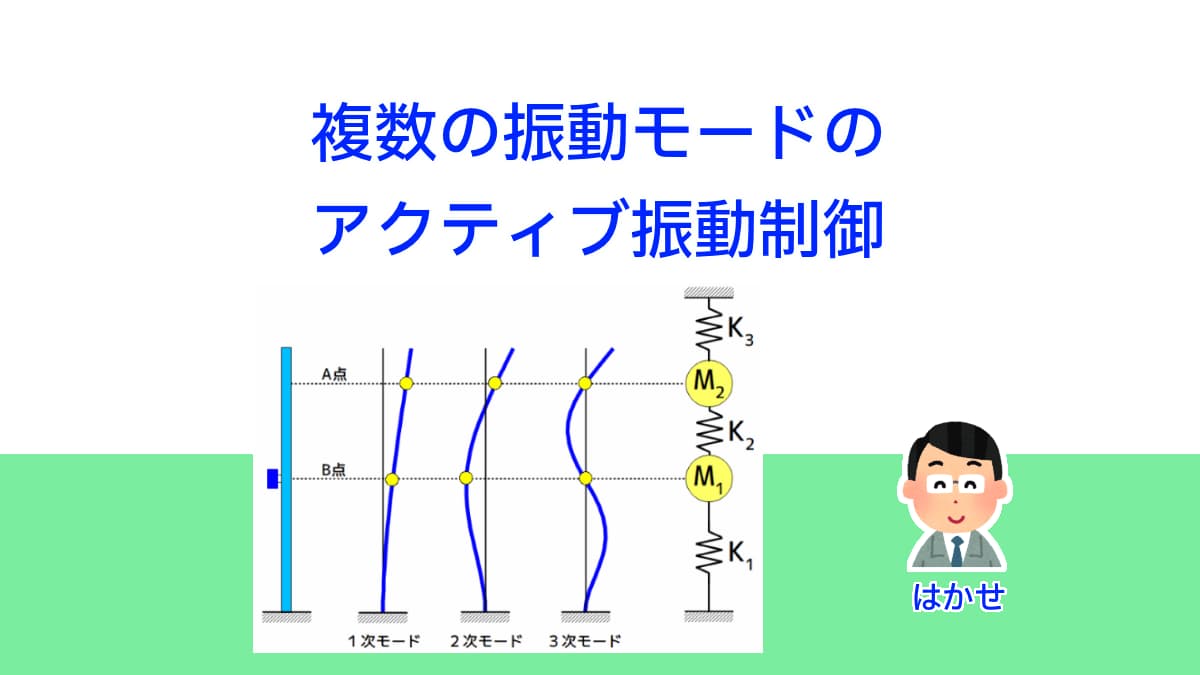
「振動モード形を利用したモデルによるタワー構造物のLQ最適制御入門」では、塔状構造物の1次の振動モードを、水平2方向同時に制御する事例を紹介しました。


ここでは、柔軟構造物の1次と2次の振動モードを2自由度系モデルを作り制振する、アクティブ振動制御について説明します。
制振対象には、分布定数系の代表例である塔状構造物を選び、多自由度系の最小次数である2自由度系の低次元化モデルを作ります。
モデリングの際、3次モードの節を低次元化モデルの質点の位置にして、塔状構造物の低次元化モデルを作成し、3次モードによるスピルオーバの発生を防止します。
LQ制御理論により制御系を設計し、シミュレーションと実験により制振効果を確認します。
塔状構造物のモデリング
実験モード解析により得られた制振対象の塔状構造物の振動モード形と低次元化物理モデルを下図に示します。
制振対象の塔状構造物は、高さ1500mm、断面が30mm×60mm、厚さ2.3mmの鉄製の中空角材からなり、下端は垂直に固定しています。
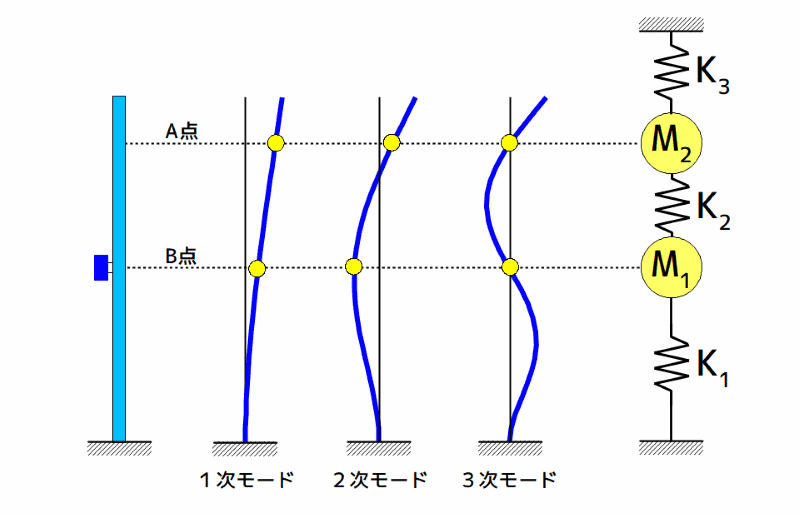
塔状構造物の振動モード形と物理モデル
図1 塔状構造物の振動モード形と物理モデル
制御系設計
制振対象の低次元化モデルとハイブリッド動吸振器からなる制御モデル(集中定数系モデル、力学モデル)の運動方程式を立て、状態方程式を導入します。
次に、LQ最適制御理論により制御系を設計します。
運動方程式と状態方程式
集中定数形モデルに基づき状態方程式を導入します。
ハイブリッド動吸振器設置位置は、制振対象の3次モードの節としますが、3次モードの節は2箇所あります。
ここでは、2次モードの制振効果を考慮して、3次モードの最大振幅点に近い節としています。
下図に、2自由度系に低次元化された制振対象とハイブリッド動吸振器の力学モデルを示します。
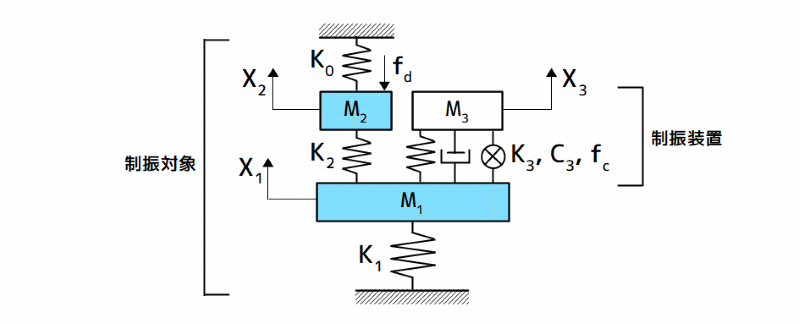
制振対象とハイブリッド動吸振器の力学モデル
図2 制振対象とハイブリッド動吸振器の力学モデル
ここで、相対変位を次式のように定義します。
$$X_d = X_3 \; – \; X_1 \tag{式-1} $$
この相対変位を用いると運動方程式は、次式で表されます。
$$\dot X_2 = \frac{K_2}{M_2} X_1 \; – \; \frac{K_0 + K_2}{M_2} X_2 \tag{式-3} $$
ここで、状態変数ベクトルを次のように定義すると、
$$\boldsymbol{X} = \begin{Bmatrix} \; \dot{X_1} \; \dot{X_2} \; \dot{X_d} \; X_1 \; X_2 \; X_d \end{Bmatrix}^T \tag{式-5}$$
状態方程式は、次式で表されます。
$$\dot{\boldsymbol{X}} = \boldsymbol{A} \boldsymbol{X} + \boldsymbol{b} \boldsymbol{u} \tag{式-6}$$
ただし、
$$\boldsymbol{b} = K_c \cdotp \begin{bmatrix} \frac{1}{M_1} & 0 & – \left( \frac{1}{M_1} + \frac{1}{M_3} \right) & 0 & 0 & 0 \end{bmatrix}^T$$
\(K_c\):制御力と制御量との関係を示す力変換係数
LQ制御理論による制御系設計
制御系設計には、LQ制御理論を用います。
ここでの設計パラメータは、次式で表される線形2次形式の評価関数\(\boldsymbol{J}\)に与える重み係数行列\(\boldsymbol{Q}\)と重み係数\(R\)になります。
$$\boldsymbol{J} = \int_0^\infty ( \boldsymbol{X}^T \boldsymbol{Q} \boldsymbol{X} + u^2 R ) \; dt \tag{式-5-7}$$
ただし、
$$\boldsymbol{Q} = diag \; \left[ \; q_1, q_2, q_3, q_4, q_5, q_6 \right]$$
ここで、
\(q_1\):質点1の速度に掛かる重み係数
\(q_2\):質点2の速度に掛かる重み係数
\(q_3\):相対速度に掛かる重み係数
\(q_4\):質点1の変位に掛かる重み係数
\(q_5\):質点1の変位に掛かる重み係数
\(q_6\):相対変位に掛かる重み係数
LQ制御理論によれば、この評価関数\(\boldsymbol{J}\)を最小にする制御量\(u\)は、次のように定式化されています。
$$u = \; – R^{-1} \boldsymbol{b}^T \boldsymbol{P} \boldsymbol{X} = \; – \boldsymbol{K} _g \boldsymbol{X} \tag{式-8}$$
ただし、
$$\boldsymbol{K} = \begin{Bmatrix} k_1, k_2, k_3, k_4, k_5, k_6 \end{Bmatrix} $$
ここに、\(\boldsymbol{P}\)は、次式のリカッチ方程式の解です。
$$\boldsymbol{P} \boldsymbol{A} + \boldsymbol{A}^T \boldsymbol{P} \; – \boldsymbol{P} \; \boldsymbol{b} \; \boldsymbol{R}^{-1} \; \boldsymbol{b}^T \; \boldsymbol{P} + \boldsymbol{Q} = 0 \tag{式-9}$$
このリカッチ方程式を解くことにより、状態フィードバックゲインを求めることができます。
制振効果の解析(シミュレーション)
重み係数による制振効果の違いについて、根軌跡図、周波数応答(伝達関数)、及び、シミュレーション(インパルス応答、時間応答)により確認します。
根軌跡図による重み係数による制振効果の比較
LQ制御理論を用いて制御系設計を行う場合、重み係数と得られる制振効果との関係が明かでないため、試行錯誤的に重み係数を決定する場合が多くなります。
そこで、根軌跡図を利用して、重み係数と得られる制振効果との関係を明らかにします。
まず、変位項と速度項による制振効果を比較し、重み係数の役割を考察します。
なお、相対変位、相対速度にかかる重み係数は、ハイブリッド動吸振器の制振性能に影響を与える重み係数です。
ここでは、制御系の基本的な傾向を明かにするため、この2つの重み係数を零(ゼロ)とし、ハイブリッド動吸振器に制約条件を与えない場合の解析を行います。
図3、図4に、それぞれ変位項、速度項に重みを掛けた場合の根軌跡図を示します。
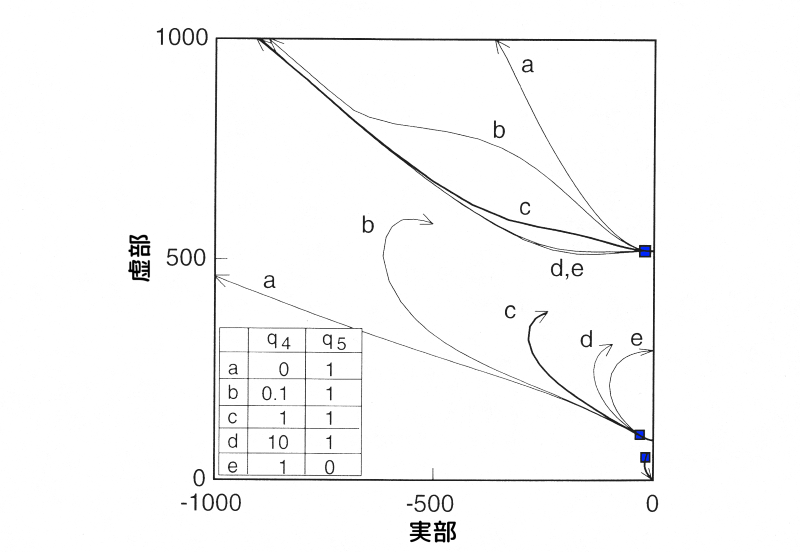
変位項に重みを掛けた場合の根軌跡図
図3 変位項に重みを掛けた場合の根軌跡図
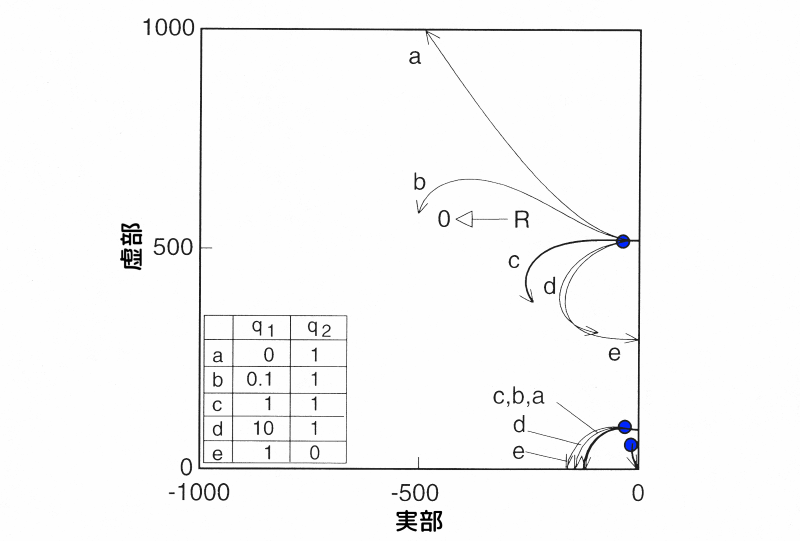
速度項に重みを掛けた場合の根軌跡図
図4 速度項に重みを掛けた場合の根軌跡図
この系においては、3個の特性根が存在します。
下側から、ハイブリッド動吸振器、制振対象の1次、2次の根です。
\(R\)を小さくする(制御を強くする)とS平面上を左方向に移動します。
図中のa~eは、図中に示す重み係数の他は、全て零の場合の重み係数を示しています。
なお、ハイブリッド動吸振器の根が虚軸から離れているのは、使用したハイブリッド動吸振器の減衰係数の影響によるものです。
以下に、各々の重み係数による根軌跡の傾向について説明します。
\(q_4 = q_5 = 1\)の場合:制振対象の変位項に重みづけ
- ハイブリッド動吸振器の根は原点に向かいます。
- 制振対象の1次と2次の根は、当初近付きます。
- 1次の根はS平面上の1点に収束し、2次の根はS平面上を左に移動します。
\(q_1 = q_2 = 1\)の場合:制振対象の速度項に重みづけ
- ハイブリッド動吸振器の根は、原点に向かいます。
- 制振対象の1次の根は、S平面上を左方向に移動し、実軸に引き込まれます。
- 2次の根は、S平面上の1点に収束します。
\(q_4 = q_5 = 1\)と\(q_1 = q_2 = 1\)の場合のひ各:制振対象の速度項と変位項の比較
変位項と速度項に重みを掛けた場合の制振効果を比較するため、以下の点をそれぞれ、□印、〇印として、図3、図4にプロットしています。
\(q_4 = q_5 = 1\)、\(R = 1 \times 10^{-8}\)
\(q_1 = q_2 = 1\)、\(R = 1 \times 10^{-4}\)
この両点の虚軸からの距離を比べると、ハイブリッド動吸振器と制振対象の1次の根の位置は、どちらの場合でもほぼ同一です。
しかし、2次の根は、速度項に重みを掛けた場合の方が虚軸より離れています。
これより、制振対象の2次モードを抑制するには、速度項に重みを掛けた方が、制振効果が大きいことが分かります。
図5に、変位項、速度項に重みを掛けた場合の周波数応答を示します。
点線が非制御、細線が変位項に重みを掛けた場合、太線が速度項に重みを掛けた場合の応答です。
なお、\(R\)は1次モードのピークが、ほぼ同程度に安定化される値を選んでいます。
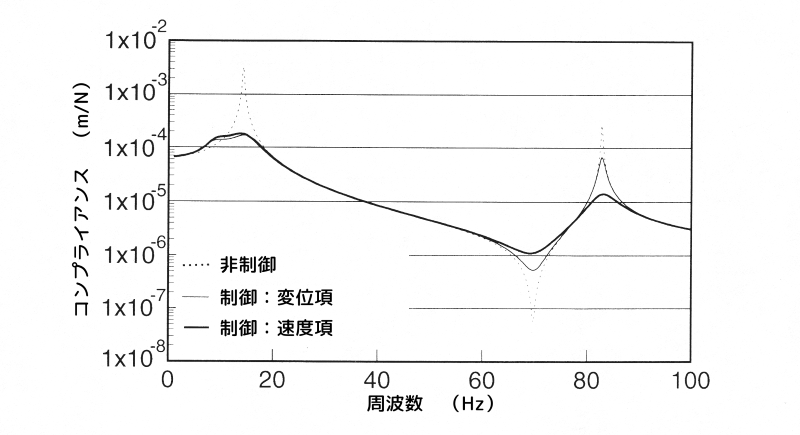
変位項と速度項に重みを掛けた場合の周波数応答の比較
図5 変位項と速度項に重みを掛けた場合の周波数応答の比較
同図より、変位項に重みを掛けた場合には2次の制振効果が十分ではなく、速度項の方が2次の制振効果に与える影響が大きいことが分かります。
図6、図7に、それぞれ変位項、速度項に重みを掛けた場合のインパルス応答(時間応答)を示します。
両図において、図(a)が質点2、図(b)が質点1、細い実線が非制御時、太い実線が制御時の応答です。
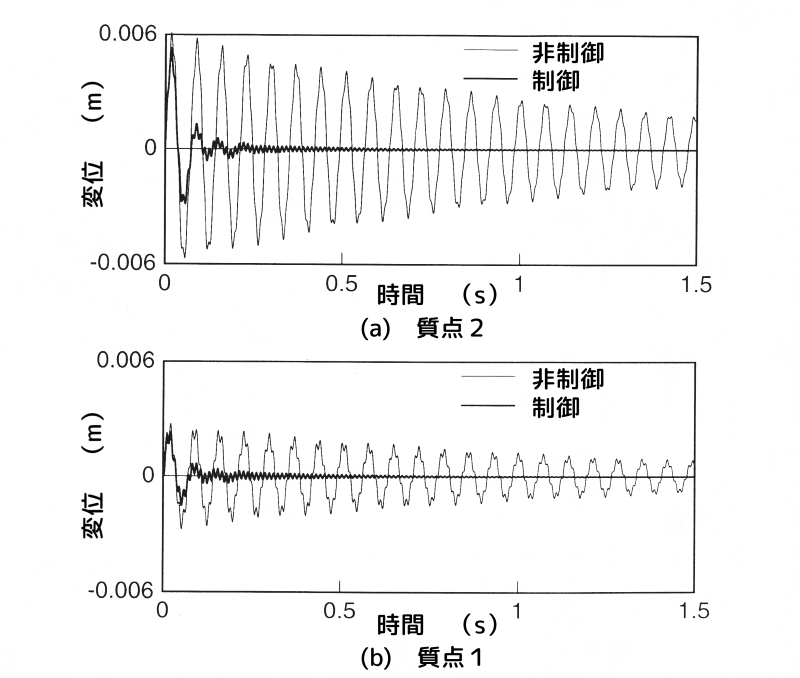
変位項に重みを掛けた場合のインパルス応答
図6 変位項に重みを掛けた場合のインパルス応答
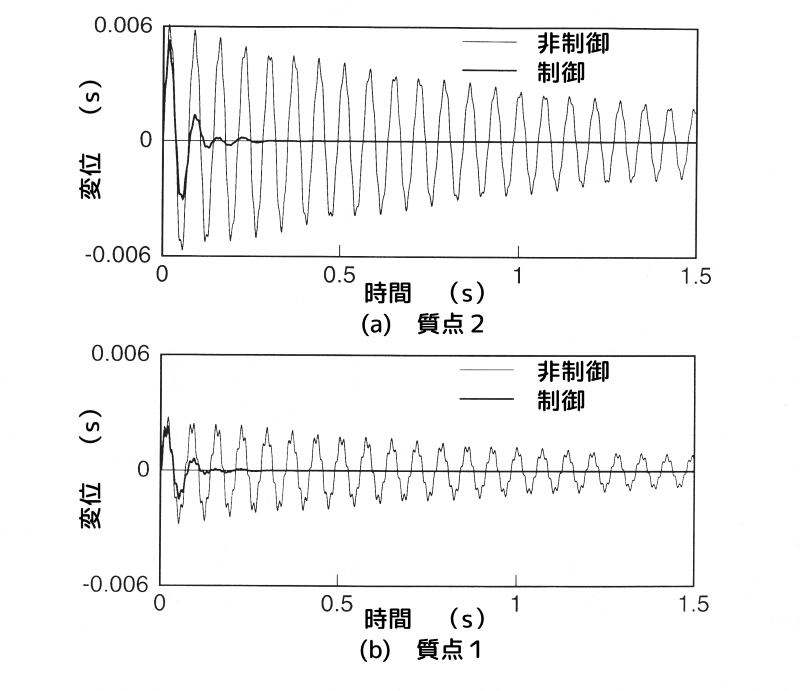
速度項に重みを掛けた場合のインパルス応答
図7 速度項に重みを掛けた場合のインパルス応答
なお、非制御時においても振動が収束しています。
これは、ハイブリッド動吸振器がパッシブ動吸振器として機能しているためです。
両図から、制御を掛けることにより、各点の振動が速やかに収束することを確認できます。
次項から、速度または変位に関する2個の重み係数の比を変化させた場合の制振効果について調べます。
\(q_4\)と\(q_5\)の比を変化させた場合
\(q_4\)と\(q_5\)の比を変えた場合においても、基本的には図4のcの場合の傾向を示します。
\(q_4\)と\(q_5\)の比を変えることにより、図3のaとeで挟まれる領域を移動します。
そこで、図8に\(q_4\)と\(q_5\)とによる制振効果の比較例として、\(R = 1 \times 10-{-8}\)の場合におけるaとeの比較を示します。
これより、2次のピークはほとんど差がありません。
しかし、1次のピークは、 aの場合の方が制振効果が高いことが分かります。
従って、\(q_4\)と\(q_5\)では、\(q_5\)の方が制振効果に与える影響が大きいことが分かります。
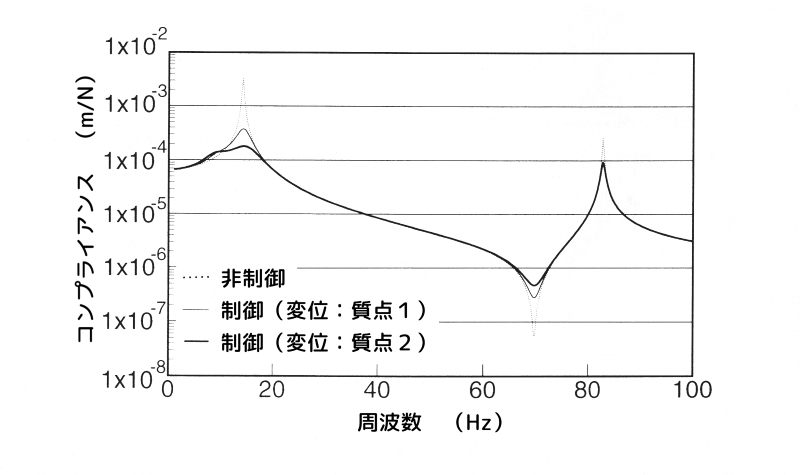
重み係数\(q_4\)と\(q_5\)による制振効果の比較
図8 重み係数\(q_4\)と\(q_5\)による制振効果の比較
\(q_1\)と\(q_2\)の比を変化させた場合
同様にして、変位に関する2個の重み係数\(q_1\)と\(q_2\)の比を変化させると次のようになります。
\(q_1\)と\(q_2\)の比を変えた場合においても、基本的には図4のcの場合の傾向を示します。
\(q_1\)と\(q_2\)の比を変えることにより、図4のaとeで挟まれる領域を移動します。
そこで、図9に、\(q_1\)と\(q_2\)による制振効果の比較として、\(R = 1 \times 10^{-4} \)の場合におけるaとeの比較を示します。
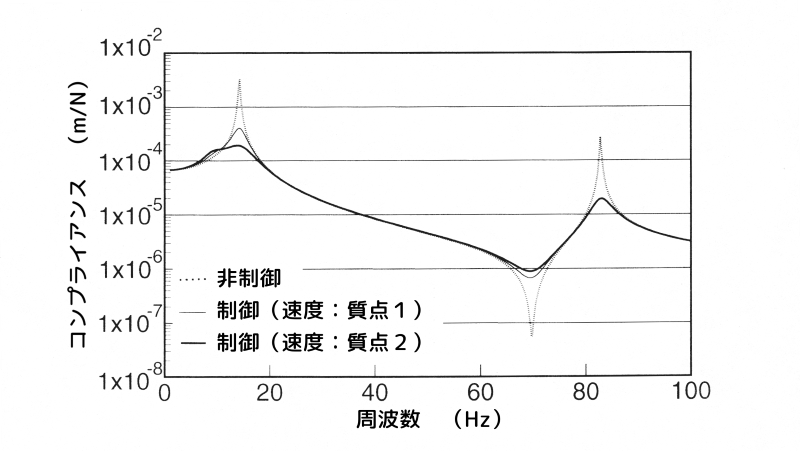
重み係数\(q_1\)と\(q_2\)による制振効果の比較
図9 重み係数\(q_1\)と\(q_2\)による制振効果の比較
これより、2次のピークはほとんど差がありませんが、1次のピークは、aの場合の方が制振効果が高いことが分かります。
従って、\(q_1\)と\(q_2\)とでは、\(q_2\)の方が制振効果に与える影響が大きいことが分かります。
振動制御実験(制振効果の確認)
実験装置及び実験方法
本実験装置の構成を下図に示します。
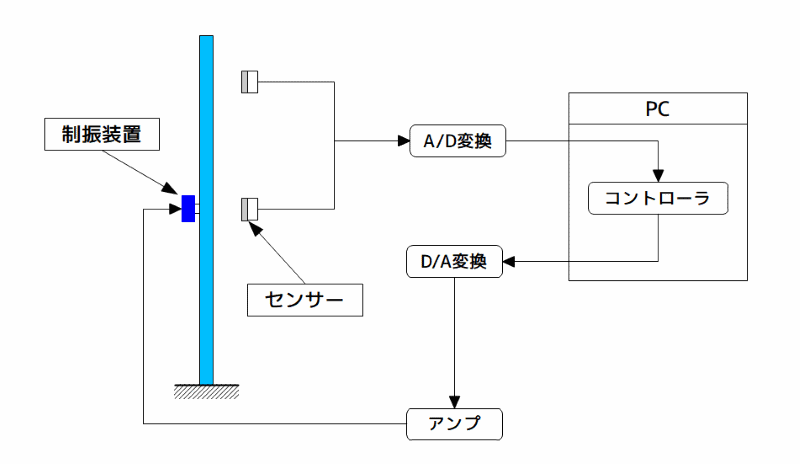
実験装置の構成
図10 実験装置の構成
なお、ハイブリッド動吸振器は、動吸振器型ハイブリッド動吸振器であり、コントローラにパソコンを使用して制御系を構成しています。
塔状構造物の3次モードの節の位置に設置された2個の変位センサは、制振対象の変位を検出し、ハイブリッド動吸振器の相対変位と共に、A/D変換器を介してコンピュータに入力され差分により速度信号を得ています。
これらの6個の状態量と、重み係数に応じて算出したフィードバックゲインにより、塔状構造物の振動制御を行なっています。
実験は、制御を掛けた状態で、塔状構造物先端をインパルス加振した場合の時間応答により、制振効果を評価します。
実験結果
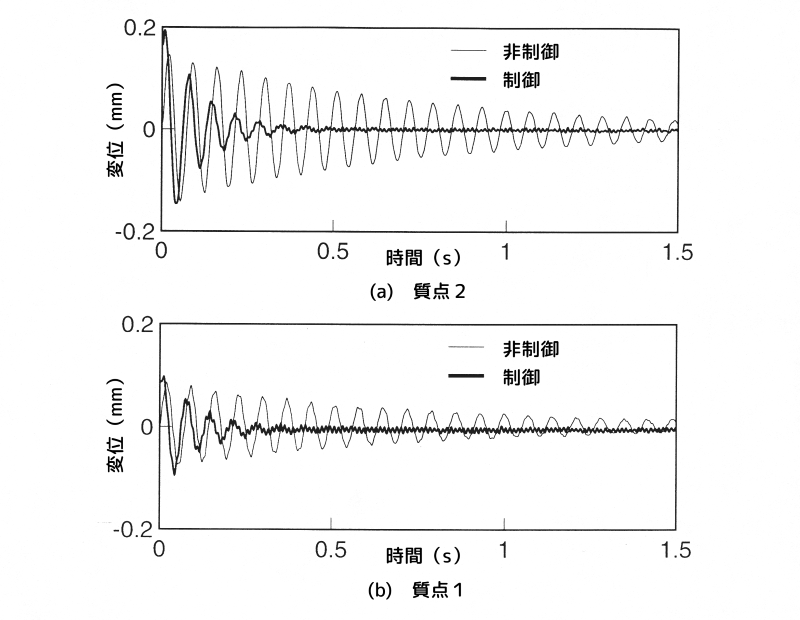
図11に、変位項に重みを掛けた場合の時間応答を示します。
$$\boldsymbol{Q} = diag \; \left[ \; 0 \; 0 \; 0 \; 1 \; 1 \; 0 \right] ,R = 0.1$$
同図(a)が質点2の変位、同図(b)が質点1の変位です。
細い実線が制御を掛けない場合、太い実線が\(R = 0.1\)で制御した場合です。
変位項に重みを掛けた場合のインパルス応答
図11 変位項に重みを掛けた場合のインパルス応答
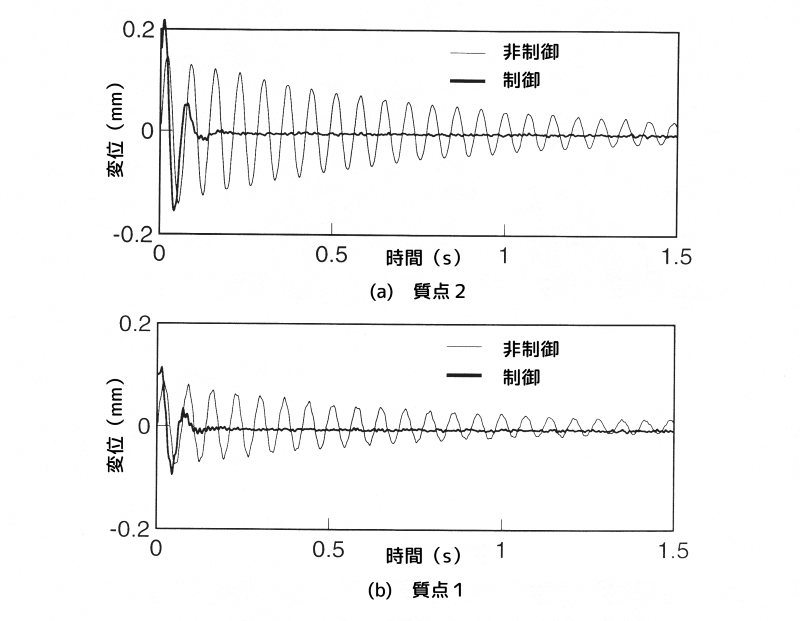
図12に、速度項に重みを掛けた場合の時間応答を示します。
$$\boldsymbol{Q} = diag \; \left[ \; 1 \; 1 \; 0 \; 0 \; 0 \; 0 \right] ,R = 100$$
同図(a)が質点2の変位、同図(b)が質点1の変位です。
細い実線が制御を掛けない場合、太い実線が\(R = 100\)で制御した場合です。
速度項に重みを掛けた場合のインパルス応答
図12 速度項に重みを掛けた場合のインパルス応答
両図において、非制御の場合においても振動が収束しています。これは、ハイブリッド動吸振器の受動的制振効果のためです。
この様に、アクティブ制御系が機能しない場合においても制振効果が失われない信頼性の高い制振装置であることが分かります。
制御を掛けることにより、構造物の振動が速やかに収束し、良好な制振効果が得られていることを確認できます。
まとめ
ここでは、柔軟構造物の1次と2次の振動モードを2自由度系モデルを使い制振する、アクティブ振動制御について説明しました。
主な項目は次の通りです。
- 塔状構造物のモデリング
- LQ制御理論による制御系設計
- 制振効果の解析(シミュレーション)
- 振動制御実験(制振効果の確認)