ここでは、タワーのような塔状構造物を対象としたアクティブ振動制御を、どの様にして実現するのかをモデリング、制御系設計、実験により説明します。
実際の振動制御については、スカイツリーのアンテナ(ゲイン塔と呼ばれていいます)の揺れを抑えるための制御が1つの例になります。制振装置は、ゲイン塔の最上部に設置されています。
なお、スカイツリーの本体部は、心柱制振と呼ばれる五重塔の技術が使われた古くて新しい振動制御方式が使われています。

スカイツリーのゲイン塔(アンテナ)
スカイツリーなどの高層建築物に振動制御(制振)が必要な理由
スカイツリーや高層ビルなどの上層部は眺望もよく、眺望そのものを付加価値としている展望フロアだけでなく、レストランやホテルとしても利用されています。

スカイツリー全景
高層階では素晴らしい景色を見ることができますが、障害物がないということでもあり、窓1枚隔てた外側の風(外界の自然)は直接感じることができないため気付きにくいのですが、地上ではほとんど風がない天気の時でも意外に強い風が吹いているそうです。
スカイツリーなどの高層ビルなどで眺望という付加価値を得るためには、次のような理由で振動(揺れ)対策が必須となっています。
- 台風や地震などの自然に対する振動対策
- 海沿いなど設置場所にもよりますが、風などによる揺れ
これらの振動対策の結果、高層建築物の揺れが抑えられ、素晴らしい景色とおいしい食事などを楽しむことができているのです。

高層建築物には振動制御(揺れを抑えること)が必要な理由について、何となくイメージできたでしょうか?
どうやって高層建築物の揺れを小さくするの?
スカイツリーや高層ビルなどの高層建造物の揺れ(振動)を、どうやって小さくするかについて説明します。
あまり高くない建造物(ビル)であれば、免震装置を使います。
例えば、
- 地盤とビル本体の間の基礎部分に免震装置を設置する。
- 建物の梁の部分に巨大なダンパーを設置する。
さらに高い建築物になると、アクティブ制振装置が使われています。
実用化されているアクティブ制振装置(実際にはパッシブ制振機能も持つハイブリッド型です)は、様々な工夫を凝らし水平2方向の振動制御を実現しています。
アクティブ制振装置の使用例としては、横浜のランドマークタワーには、多段振り子型のチューンドマスダンパと呼ばれる制振装置が使われています。
ここで説明する振動制御の概要について
ここでは、スカイツリーや高層ビルのようなタワー構造物と同様の振動特性を示すシンプルな塔状構造物を振動制御対象に選んでいます。
塔状構造物の振動制御について、シミュレーションと実験により以下の内容について説明していきます。
- 制振対象(塔状構造物)のモデリング
- 振動モード形を利用した「不可制御・不可観測性を活用した低次元化モデル作成法」による制振対象の低次元化モデルの作成
- 制御系設計とシミュレーション
- 現代制御理論の1つであるLQ制御理論
- 制振装置として、2次元ハイブリッド動吸振器を使っています。
- 振動制御のシミュレーション
- 振動制御実験による制振効果の確認
振動制御を実現する主なプロセス
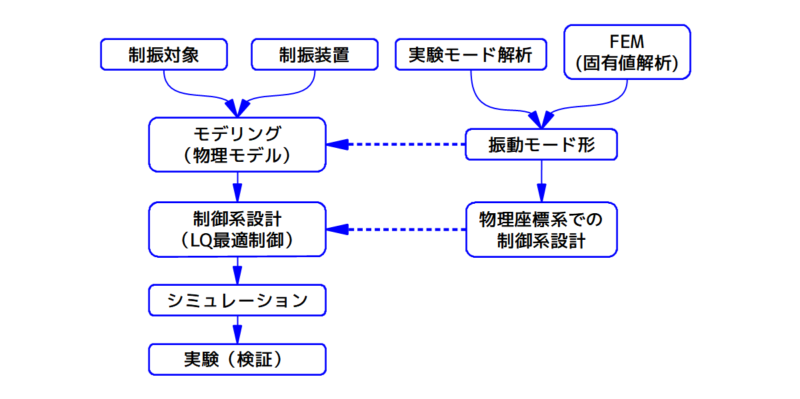
振動制御の主なプロセスをフローにしてみると下図の様になります。
なお、この記事ではFEMについては触れていませんが、FEM(固有値解析)の解析結果として振動モード形を使います。
振動制御の主なプロセスフロー
図 振動制御の主なプロセスフロー
制振対象の塔状構造物
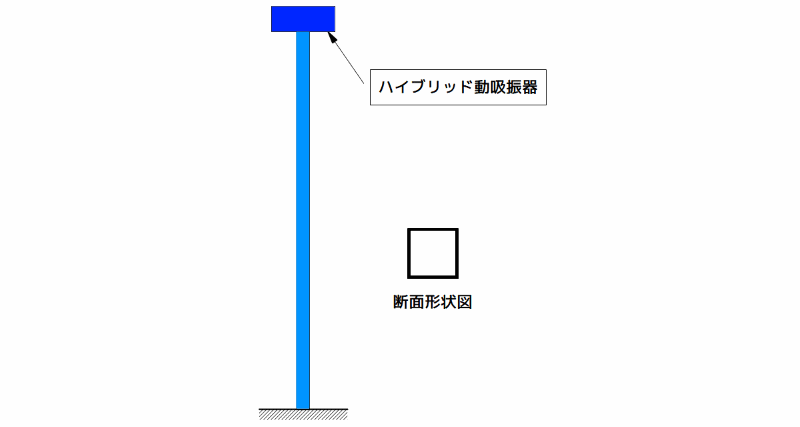
制振対象には、タワーの様な高層建築物と分布定数系的振動特性を示す代表例である塔状構造物として、高さ1.5m、断面が50×50mm、厚さ2.3mmの鋼製角パイプ(中空の鋼製角柱材)を選び、角パイプ下端を垂直にベースプレートに溶接し、これを定盤に固定しています。

タワーの様な高層建築物は、柔軟構造物、分布定数系構造物などとも呼ばれますが、ここでは塔状構造物と呼んでいます。
下図に塔状構造物の概要図を示します。
塔状構造物の概要(振動制御実験の対象)
図 塔状構造物の概要
この塔状構造物は、水平2方向で同様の振動特性を示します。
水平2方向の制御を実現するため、詳しくは後述します2次元ハイブリッド動吸振器を、制振対象の先端(最上部)に設置しています。
塔状構造物のモデリング
制振対象の制振対象の低次元化モデルの作り方について説明します。
ここでは、水平2方向をそれぞれ、X軸、Y軸と呼ぶことします。
制御する振動モードは、制振対象のX軸とY軸の1次の振動モードとします。
振動モード形の節と腹に着目した「不可制御・不可観測を活用した低次元化物理モデル作成法」により、X軸とY軸それぞれの1自由度系の低次元化モデルを作成します。
この際、低次元化によって打ち切られた直後の高次(周波数が高い)モードである2次モードによるスピルオーバー(制御を掛けたことにより、不安定になってしまう現象のこと)を防止するため、センサー設置位置を2次モードの節とします。

スピルオーバーとは、制御を掛けたことにより、不安定になってしまう現象のことです。
これにより、2次の振動(固有振動数、共振周波数)を検出しなくなるため(不可観測)、スピルオーバーーを防止することができます。
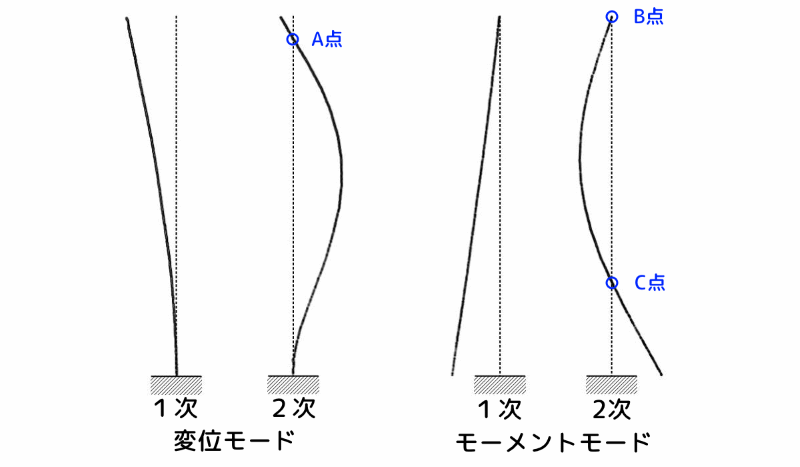
下図に、塔状構造物の1次と2次の振動モード形を示します。
塔状構造物の1次と2次の振動モード形
図 塔状構造物の1次と2次の振動モード形
2次モードの振動の節(上図の青丸の部分)は、変位モードでは塔状構造物の先端付近のA点、曲げモーメントモードでは先端のB点と下部のC点にあります。
ここでは変位センサーとして歪(ひずみ)ゲージを使うため、曲げモーメントモードの振動モード形を利用します。
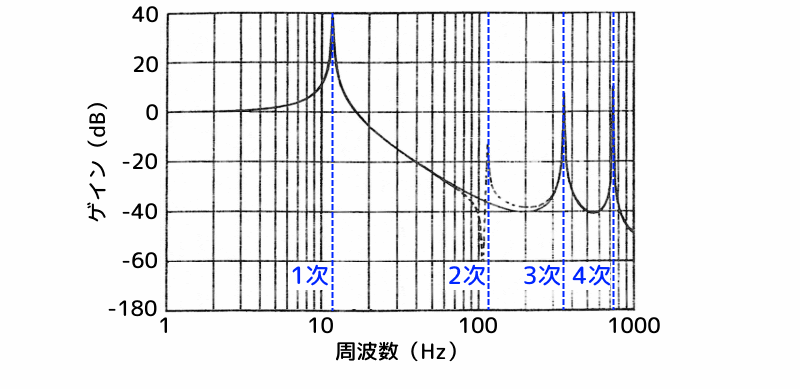
下図は、構造物の先端を加振して、2次モードの節(上図のC点)に張り付けた歪ゲージにより、変位を計測したときの周波数応答の1例です。
塔状構造物の振動モード形(変位モードとモーメントモード)
図 2次モードの節における曲げモーメントの周波数応答の比較
実線は2次モードの節、破線は2次モードの節から外れた場合の周波数応答です。
2次モードの節にセンサーを取り付けた場合、上図の2次の青の破線(約110Hz)上に現われるべき2次モードの共振ピークげ検出できていません。これは、計測信号に塔状構造物の2次の固有振動数が含まれていないということになります。
上図の3次の青の破線(約350Hz)にある3次モードの固有振動数は検出されています。周波数の離れた高次モードは、制御系にほとんど影響を与えないと考えられますが、制御系への影響については、後述する実験で確認します。
なお、仮に高次モードの影響が懸念される場合には、ローパスフィルタを使って取り除くといった対策をします。
ここで説明した2次の振動モードの不可観測性を利用して、塔状構造物を1自由度系に低次元化します。
なお、この構造物は対称構造なので、水平2方向とも同様の特性(固有振動数)となっています。
LQ制御理論による制御系設計
制御系設計には、現代制御理論の1つであるLQ制御理論を使います。
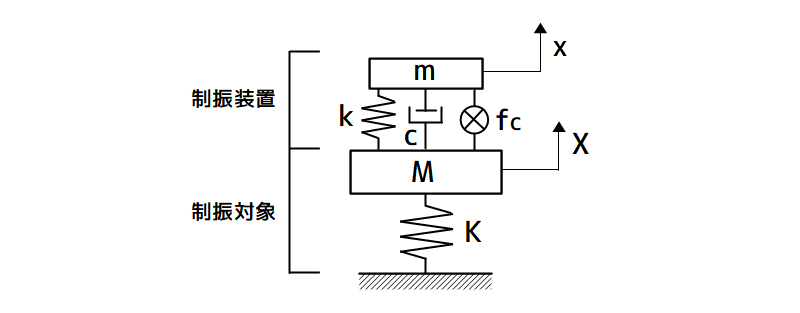
下図に、塔状構造物先端で1自由度系に低次元化した制振対象とハイブリッド動吸振器の力学モデルを示します。
制振対象とハイブリッド動吸振器の力学モデル
図 制振対象とハイブリッド動吸振器の力学モデル
ただし、
M、K:制振対象の質量、ばね定数
m、k、c:ハイブリッド動吸振器の質量、ばね定数、減衰係数
fc :制御力

力学モデルを設定し、運動方程式(状態方程式)を立てれば、制御系設計ツールによるどんな制御をかけるかに進めます。
なお、制振対象である塔状構造物をX軸とY軸の2方向で低次元化していますが、両軸とも同様の振動特性を示しているため、同じ低次元化モデルを使用しています。
ここで、相対変位を次式のように定義します。
$$X_d = x – X$$
この相対変位を用いると、制御対象(塔状構造物)と制振装置(ハイブリッド動吸振器)の力学モデルの運動方程式は、次式となります。
$$\ddot X = – \frac KM X + \frac kM X_d + \frac cM \dot X_d + \frac {f_c} M$$
ここで、状態変数ベクトルを次のように定義すると、
$$\begin{eqnarray}
\mathbf{X}\ = \left( \begin{array}{c} \dot X \\ \dot X_d \\ X \\ X_d \end{array} \right) \end{eqnarray}$$
状態方程式は、次式で表されます。
$$\mathbf{\dot X}\ = \mathbf{A}\ \mathbf{X}\ + \mathbf{b}\ \mathbf{u}\ $$
ただし、 $$\begin{eqnarray} \mathbf{X}\ = \left( \begin{array}{cccc} 0 & \frac cM & – \frac KM & \frac kM \\ 0 & – \left(\frac cM + \frac cm\right) & \frac KM & – \left(\frac kM + \frac km\right) \\ 1 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 \end{array} \right) \end{eqnarray}$$
$$\begin{eqnarray}
\mathbf{b}\ = K_c \cdot \left( \begin{array}{c} \frac 1M \\ – \left(\frac 1M + \frac 1m\right) \\ 0 \\ 0 \end{array} \right) \end{eqnarray}$$
\(Kc\):制御力と制御量の関係を示す力変換係数
この場合の設計パラメーターは、次式で表される線形2次形式の評価関数\(J\)に与える重み係数行列\(\mathbf{Q}\)と重み係数\(R\)になります。
$$\mathbf{J}\ = \displaystyle \int_0^\infty – \left(\ X^T Q X + u^2R \right) dt$$
ただし、
$$\mathbf{Q}\ = diag \begin{bmatrix} q_1 & q_2 & q_3 & q_4 \end{bmatrix}$$
ここで、
\(q_1\) 、\(q_2\):速度、相対速度に掛かる重み係数
\(q_3\) 、\(q_4\):変位、相対変位に掛かる重み係数
LQ制御理論によれば、この評価関数\(J\)を最小にする制御量\(u\)は、次のように定式化されており、リカッチ方程式を解くことによりフィードバックゲインを決定することができます。
$$u = – R^{-1} \mathbf{P}\ \mathbf{P}\ = – \mathbf{K}\ \mathbf{X}\ $$
ここに、\(P\)は、次のリカッチ方程式の解です。
$$\mathbf{P}\ \mathbf{A}\ + \mathbf{A}^T\ \mathbf{P}\ – \mathbf{P}\ b R^{-1} b \mathbf{P}\ + \mathbf{Q}\ = 0 $$

数式だけみていると難しそうですが、MATLABなどの制御系設計ツールを使うと、フィードバックゲインは一瞬で出てきます。
振動制御実験
振動制御実験結果を説明する前に、本実験で使用した2次元ハイブリッド動吸振器について説明します。
2次元ハイブリッド動吸振器について
ハイブリッド動吸振器は、アクティブ動吸振器の持つ高い制振性能とパッシブ動吸振器の持つ高い信頼性を合わせ持ちます。
このため、何等かの理由によりアクティブ動吸振器の機能が停止した場合においても、パッシブ動吸振器の機能により安全性を確保する信頼性の高い構造と言えます。
また、塔状構造物の様に平面2方向で同様の振動特性を有する構造物には、X 軸とY軸の水平2方向の制御が可能な制振装置が必要となります。
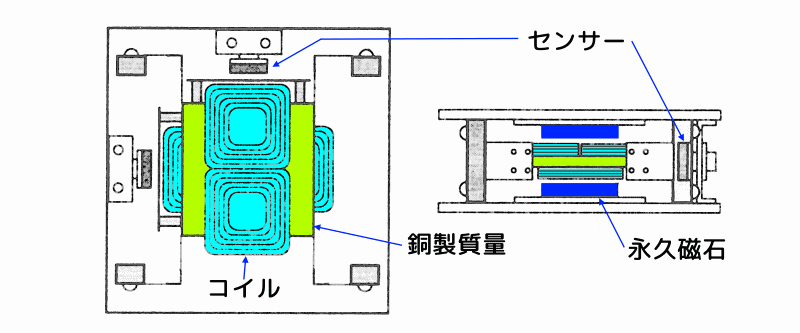
下図に、水平2方向の振動制御に使える2次元ハイブリッド動吸振器の構造を示します。
2次元ハイブリッド動吸振器の構造
図 2次元ハイブリッド動吸振器の構造
上図において、左側の図が上方から、右側の図が側面から見た図です。
銅製のアクティブ質量(上図の黄緑色の部分)は、4個のL字型板ばねで支持されており、水平面内を自由に動けるようになっています。

機械的接触(摩擦)がない構造なので、シミュレーションと実験との比較がしやすいというメリットもあります。摩擦や減衰を考慮するとそれが研究テーマの1つになってしまいます。
アクティブ質量と構造物本体との相対変位は、X軸とY軸方向の2個の変位センサーより検出します。
アクティブ動吸振器としての機能
アクティブ動吸振器としての機能は、電磁力を利用しています。
アクティブ質量の両面に各々一対取り付けられたロ型の駆動コイルが、上下に置かれた永久磁石が作る磁場内で磁束を直角によぎる構造となっています。
アクティブ質量の上面と下面に設置したコイルに与える電流の向きを直交させることにより、アクティブ質量に電磁力による水平2方向の動きを与えることができます。
パッシブ動吸振器としての機能
パッシブ動吸振器としての機能は、磁気減衰力を利用しています。
アクティブ質量は、導体である銅で作られています。
アクティブ質量が上下の永久磁石により作られた磁場内で、磁束と直交して移動する時に渦電流が発生し、移動方向と逆向きの磁気減衰力が発生します。この磁気減衰力により、パッシブ動吸振器としての機能を実現しています。
この様に、アクティブ質量には磁気減衰力と電磁力が同時に作用する構造となっており、受動的動吸振器とアクティブ動吸振器の特性を兼ね備えたハイブリッド動吸振器を実現しています。
また、ここで紹介している2次元ハイブリッド動吸振器は、使用する永久磁石が一対で済み、1個のアクティブ質量で2方向の運動を制御することが可能なため軽量化と構造の簡素化を同時に実現しています。
実験装置及び実験方法
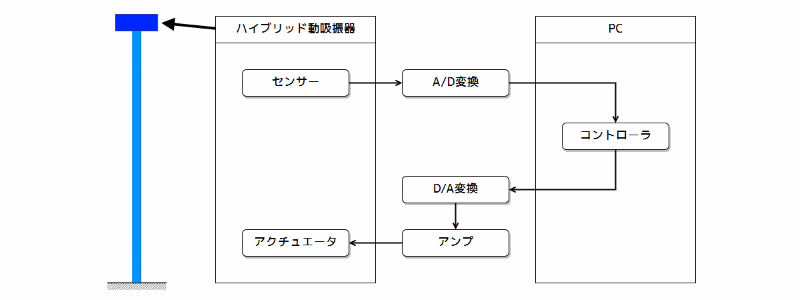
実験装置の構成を下図に示します。
塔状構造物の振動制御実験装置の構成
図 塔状構造物の振動制御実験装置の構成
X軸とY軸方向の制御のために、2台のコントローラを使用しています。
各コントローラは、歪ゲージで検出された塔状構造物の変位信号と、変位センサーで検出された相対変位信号を、各々の速度信号に変換(実際はサンプリング時間ごとの差分)し、これらの4つの信号をフィードバックして制御信号を作り、各軸方向の駆動コイルに制御電圧を出力します。
実験では、構造物上端をインパルス加振し、この時の時間応答を評価します。
等価質量同定法により制振対象の等価質量と等価剛性、2次元ハイブリッド動吸振器の物理定数を求めています。
実験結果(2次元ハイブリッド動吸振器による制振)
塔状構造物の先端を45°の方向にインパルス加振した時の実験結果(時間応答)について説明します。
塔状構造物単体の場合
下段がX軸、上段がY軸の時間応答です。
インパルス加振により発生した振動が続いています。
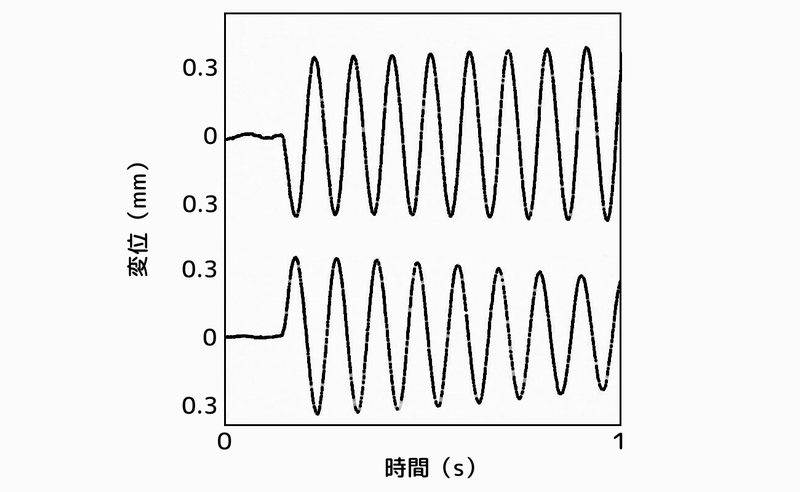
塔状構造物の応答:2次元ハイブリッド動吸振器なし
図 時間応答:ハイブリッド動吸振器なし
ハイブリッド動吸振器設置(アクティブ制御なし)の場合
下段がX軸、上段がY軸の時間応答です。
ハイブリッド動吸振器なしの場合と比べると、インパルス加振による振動が小さくなっていいるのですが、パッシブ動吸振器としての機能が十分に発揮されているとは言えない結果となっています。
パッシブ動吸振器としての効果を高めるためには、例えば、アクティブ質量に取り付けられたコイルと永久磁石との間隔を狭めることにより、磁気減衰力が大きくなることで解決することができます。
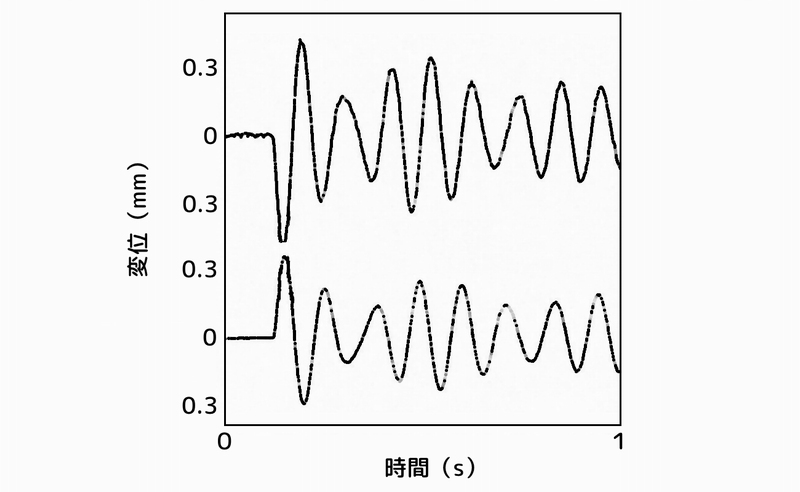
塔状構造物の応答:2次元ハイブリッド動吸振器付きで制御なし
図 時間応答:ハイブリッド動吸振器設置、制御なし
ハイブリッド動吸振器設置(アクティブ制御)の場合
下段がX軸、上段がY軸の時間応答です。
制御をONにした状態で、インパルス加振をした結果です。
X軸、Y軸方向共に、加振による揺れの1個め(1波長)から振動が小さくなっていることを確認できます。
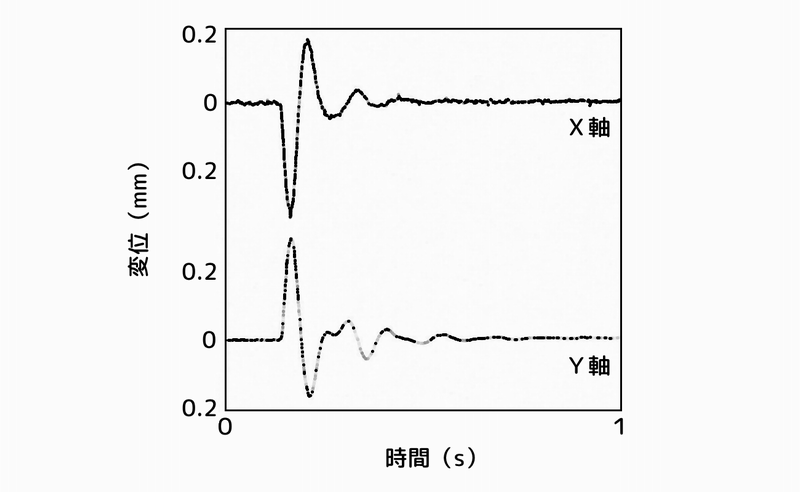
塔状構造物の応答:2次元ハイブリッド動吸振器でアクティブ制御
図 時間応答:ハイブリッド動吸振器設置、制御ON
まとめ
スカイツリーの様な塔状構造物の振動制御について、鋼製の塔状構造物を例に、実験とシミュレーションにより以下の項目について説明しました。
- 振動モード形を利用した制振対象の低次元化モデル作成方法
- LQ制御理論による制御系設計
- 実験で使用した2次元ハイブリッド動吸振器の構造
- 実験結果
- パッシブ動吸振器としての制振効果
- アクティブ動吸振器としての制振効果