このブログで紹介している振動制御の事例では、等価質量同定法を使い、制振対象の任意の点で物理モデルの等価質量を求めています。
振動モード形を利用したモデルによるタワー構造物のLQ最適制御入門
ここでは、等価質量同定法について説明します。
等価質量感応法(等価質量同定法)とは
等価質量感応法とは、
測定点の等価質量が小さいほどその点の感度が高く、
質量を付加することにより固有振動数が敏感に変化すること
を利用した感度解析法の一種です。

説明は難しそうな感じを受けるかもしれませんが、等価質量を求める方法はシンプルな方法なので、読み進めていただけると幸いです。
等価質量感応法は、1自由度等価質量感応法と多自由度等価質量感応法とに分類されます。
ここでは、以下について説明します。
- モード形と等価質量との関係
- 1自由度等価質量感応法
- 多自由度等価質量感応法
振動モード形と等価質量
下図に示すN自由度系において、注目するi次モードの固有ベクトルを次式で表します。
$$ \boldsymbol{x}_i^T = \begin{Bmatrix} x_1 & x_2 & \ldots & x_j & x_N \end{Bmatrix} \tag{式-18}$$
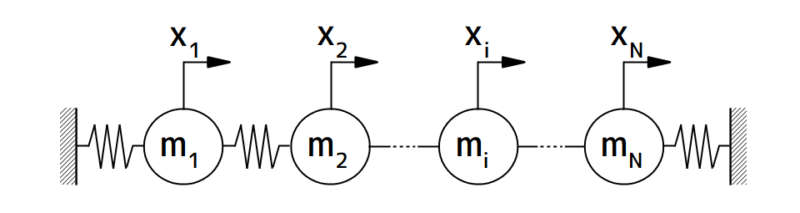
i次モードで振動するN自由度系モデル
図1 i次モードで振動するN自由度系モデル
また、各質点の速度は、\(\rho x_1\)、\(\rho x_2\)、\(\ldots\)、\(\rho x_i\)、\(\ldots\)、\(\rho x_N\)(ここに\(\rho\)は係数)なので、この状態で運動している系全体の運動エネルギは次式で表すことができます。
一方、モード解析ではN自由度系を連成のないN個の1自由度系の集合(集まり)と考えるので、図1のN自由度系を図2に示すN個の1自由度系の集合と考えます。
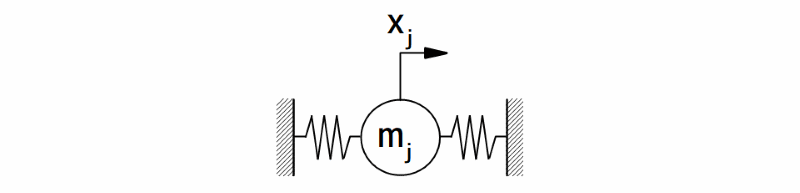
i次モードのj点における1自由度系モデル
図2 i次モードのj点における1自由度系モデル
ここで、この中の質点jに注目して、その点が図1のj点と全く同じ運動をしていると考えると、そのときの運動エネルギーは次式で表されます。
$$T_j = \frac{1}{2} M_j \begin{pmatrix} \rho x_j\end{pmatrix}^2 \tag{式-20}$$
ここで、\(M_j\)をj点で見たi次モードのj点における等価質量と定義します。
\(T_{all} = T_j\)とおけば、(式-19)、(式-20)から等価質量\(M_j\)は、次式で表されます。
これらのことから次のことが分かります。
- あるモードの振動の腹(モードの最大振幅点)では、そのモードの等価質量が最小となる。
- この位置は外乱に最も影響され易いが、制振装置を設置すれば最大の制振効果を得ることができます。
- あるモードの振動の節(モードの振幅が零の点)では、そのモードの等価質量は無限大となる。
- つまり、振動の節では外力の干渉を受けることがありません。
1自由度等価質量同定法
振動系の質量を連続系のままで同定する際に便利なのが、対象とする構造物のアクチュエータ設置場所などの任意点に既知の質量を付加し、固有振動数の変化から対象とするモードの任意点における等価質量を求める質量感応法です。
1自由度質量感応法とは、付加質量を取付けた点で1自由度系にモデル化し、その点の等価質量を求める方法です。
下図に1自由度質量感応法のイメージを示します。
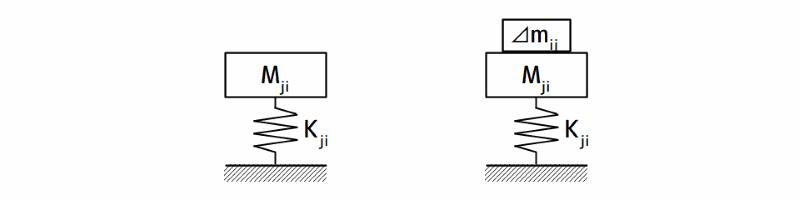
1自由度等価質量感応法のイメージ
図3 1自由度等価質量感応法のイメージ
この場合、i次モードのj点の等価質量\(M_j\)は、次式で表されます。
$$M_{ji} = \Delta m_{ji} \frac{\omega_{ji}^2}{\Omega_i^2 – \omega_{ji}^2} \tag{式-22}$$
ただし、
\(\Delta m_{ji}\):i次モードのj点に付加された既知の質量
\(\Omega_i\):元の振動系のi次の固有振動数
\(\Omega_{ji}\):j点に\(\Delta m_{ji}\)が付加されたことにより変化したi次モードの固有振動数
つまり、制振対象の固有振動数と、既知の質量を付加した際の固有振動数は次式となります。
$$\Omega_{ji} = \sqrt{\frac{K_{ji}}{M_{ji}}} $$
$$\omega_{ji} = \sqrt{\frac{K_{ji}}{M_{ji} + \Delta m_{ji}}} $$
1自由度等価質量同定法の注意点
1自由度等価質量同定法を使う際には、次の理由から付加質量の選定には注意が必要です。
- 付加質量が小さ過ぎれると
- 固有振動数の変化も微少となり、等価質量の同定に誤差が生じやすくなります。
- 逆に付加質量が大き過ぎると
- 隣接するモード間の連成の影響により誤差が生じたり、対象とするモードが変化して正しい値を得ることが困難になります
そこで、付加質量は小さ過ぎず固有振動数に変化が出るものにすることがポイントとなります。
他にも、
- 計測器(FFTアナライザ)の周波数分解能も高くしておくことが誤差を小さくするのに有効です。
この様に、付加質量の選定は、経験的要素に大きく左右されます。
経験にあまり左右されない、次の方法を紹介します。
- 数種類の付加質量を対象とする構造物に取り付けることによりモード間の連成による影響を打ち消す方法
仮に、モード間に連成の影響がある場合、付加質量が大きくなるに従い算出される等価質量も大きくなります。
そこで付加質量を横軸、算出された等価質量を縦軸に取り、この関係をプロットしてモード間の連成の度合いを明らかにし、かつ付加質量が零のときの等価質量を読めば、それが求めたい等価質量となります。
このように、1自由度質量感応法はモード間の連成を考慮していないため、次に、モード連成の影響も考慮した多自由度質量感応法について説明します。この手法を用いれば付加質量を取り替える手間がなくなり、より簡単に等価質量を求めることができます。
多自由度等価質量同定法
多自由度質量同定法は、与えられた構造物についてあらかじめ各モードの腹を1とする固有モードと固有振動数を求めておき(正規化と言います)、その構造物の1点に既知の質量を付加して生ずる固有振動数の変化から、一度に各モードの腹の等価質量を求める方法です。
ここで、iモードの腹における等価質量\(M_i\)は、次式によって求めることができます。
ただし、
$$A(\omega_i) = \prod_{i=1}^N ( \Omega_i^2 – \omega_i^2 ) $$
$$B_r ( \omega_i ) = – \omega_i^2 \Delta m_{ij} ( \phi_{jr} )^2 \prod_{i=1 \\ i \neq r}^N ( \Omega_i^2 – \omega_i^2 )$$
\(\Omega_i\):構造物のj点に付加質量\(\Delta m_{ji}\)が取付けられる前の1~N次の固有振動数
\(\omega_i\):構造物のj点に付加質量\(\Delta m_{ji}\)が取付けられた後の1~N次の固有振動数
\(\phi_{ji}\):i次モードのj点におけるモード成分
まとめ
ここでは、物理座標系でのモデリングと制御設計を行うために、制振対象の任意の位置における等価質量を求める等価質量同定法について、以下の項目について説明しました。
- モード形と等価質量との関係
- 1自由度等価質量同定法
- 多自由度等価質量同定法