「振動モード形を利用したモデルによるタワー構造物のLQ最適制御入門」では、振動モード形を利用してモデリングを行い、現代制御理論(LQ最適制御)により制御系を設計し、シミュレーションと実験により、塔状構造物の振動制御(制振)方法について説明しました。
モデリングについては、「振動モード形を利用したモデリング入門」で説明しました。
ここでは、現代制御理論の1つであるLQ最適制御について、一般的な数値解析結果を得るため、無次元化状態方程式を使った制御系設計方法について説明します。
制振対象は平行板ばね構造物とし、アクティブ動吸振器により、制振対象の1次と2次の振動モードを制御します。
現代制御理論のメリットと課題
現代制御理論は、システムを状態方程式で表現した後に、望ましい評価関数を最小にする意味での最適制御という概念に基づき、理論的に制御系を設計するため、多変数系を理論的に扱うことができます。
現代制御理論には、多入力・多出力の制御系を扱えるメリットがある反面課題もあります。
例えば、現代制御理論の1つであるLQ制御理論は、線形2次形式の評価関数を最小にすることにより、制御性能及び制御入力の設計要求を同時に満足させるフィードバックゲインを決定することができます。
しかし、設計パラメータである重み係数と制振効果との関係が明らかでないため、試行錯誤的に重み係数を決定しているのが現状です。
そこで、根軌跡図を活用することにより、所望の制振効果を得られる重み係数(行列)の決め方を紹介します。
また、最適制御理論は、システムを状態方程式で表現した後に、理論的に制御系を設計するため、良好な制御系を設計するためには、良好な振動系のモ デリングが必須です。
ここでは、「振動モード形を利用したモデリング入門」により作成した低次元化モデルを用いて、現代制御理論により制御系を設計する方法について説明します。
主な項目は次の通りです。
- 運動方程式を状態方程式表示
- 状態方程式と可制御・可観測性との関係
- LQ制御理論
- 制御系設計例
- アクティブ動吸振器による2自由度系の制御系設計法について説明します。
- ここで説明している振動制御法の有効性を、数値解析と実験により確認します。
運動方程式と振動制御系
一般に、アクティブ制振装置を含むN自由度系の運動方程式は、次式で表されます。
$$\boldsymbol{M} \ddot{\boldsymbol{x}} + \boldsymbol{C} \dot{\boldsymbol{x}} + \boldsymbol{K} \boldsymbol{x} = \boldsymbol{K} \boldsymbol{u} + \boldsymbol{K}_d \boldsymbol{w} \tag{式-1}$$
ただし、
\(\boldsymbol{x}\):変位ベクトル
\(\boldsymbol{M}\):質量行列
\(\boldsymbol{C}\):減衰行列
\(\boldsymbol{K}\):剛性行列
\(\boldsymbol{u}\):制御量ベクトル
\(\boldsymbol{w}\):外力ベクトル
\(\boldsymbol{K}\):制御力係数ベクトル
\(\boldsymbol{K}_d\):外乱力係数ベクトル
\(i\)、\(j\):制御力及び外乱力の個数
ここで、状態変数ベクトルを次のように定義します。
$$\boldsymbol{X} = \begin{Bmatrix}{\dot{x} \\ x} \end{Bmatrix} \tag{式-2}$$
この状態変数ベクトルを用いると、制振対象の状態方程式は次式となります。
$$\dot{\boldsymbol{X}} = \boldsymbol{A} \boldsymbol{X} + \boldsymbol{b} \boldsymbol{u} + \boldsymbol{E} \boldsymbol{w} \tag{式-3}$$
ただし、
$$\boldsymbol{A} = \begin{bmatrix} – \boldsymbol{M}^{-1} \boldsymbol{C} & – \boldsymbol{M}^{-1} \boldsymbol{K} \\ \boldsymbol{I}_{N,N} & \boldsymbol{0}_{N,N} \end{bmatrix}$$
$$\boldsymbol{B} = \begin{Bmatrix} \boldsymbol{M}^{-1} \boldsymbol{K}_f \\ \boldsymbol{0}_{1,N} \end{Bmatrix}$$
$$\boldsymbol{E} = \begin{Bmatrix} \boldsymbol{M}^{-1} \boldsymbol{K}_d \\ \boldsymbol{0}_{1,N} \end{Bmatrix}$$
\(\boldsymbol{0}_{i,j}\):i行j列の零行列
\(\boldsymbol{I}_{i,j}\):i行j列の単位行列
状態変数ベクトルは、2x1の要素よりなりますが、実際に観測する状態変数の数をp個とすれば、観測ベクトルは次式で表されます。
$$\boldsymbol{y} = \boldsymbol{C} \boldsymbol{X} \tag{式-4}$$
ただし、
\(\boldsymbol{C}\):px2の観測行列
ここで、次式の様な状態フィードバックを行うことにします。
$$\boldsymbol{u} = – \boldsymbol{K}_g \boldsymbol{X} \tag{式-5}$$
ただし、
\(\boldsymbol{K}_g\):jx2のフィードバックゲイン行列
この状態フィードバックゲインをLQ制御理論により求めることで、漸近安定の保証された制御系を構成することができます。
LQ制御理論
LQ制御理論により制御系を設計する場合、設計パラメータは、次式の2 次形式評価関数\(\boldsymbol{J}\)に与える重み係数行列\(\boldsymbol{Q}\)と重み係数行列\(\boldsymbol{R}\)になります。
$$\boldsymbol{J} = \int_0^\infty ( \boldsymbol{X}^T \boldsymbol{Q} \boldsymbol{X} + \boldsymbol{u}^2 \boldsymbol{R} ) \; dt \tag{式-6}$$
ここで、評価関数を次式のように表します。
$$\boldsymbol{J} = \boldsymbol{J}_x + \boldsymbol{J}_u \tag{式-7}$$
ただし、
\(\boldsymbol{J}_x = \int_0^\infty \boldsymbol{X}^T \boldsymbol{Q} \boldsymbol{X} \; dt\)
\(\boldsymbol{J}_u = \int_0^\infty \boldsymbol{u}^2 \boldsymbol{R} \; dt\)
ここで、\(\boldsymbol{J}_x\)は状態変数の2乗積分誤差であり、制御性能を表しています。
一方、\(\boldsymbol{J}_u\)は入力変数の2乗積分値となっており、制御に必要とされるエネルギを表しています。
\(\boldsymbol{J}_u\)と\(\boldsymbol{J}_u\)を同時に小さくできるのであれば、それが良い制御系と言うことができます。
しかし、\(\boldsymbol{J}_u\)と\(\boldsymbol{J}_u\)に要求されている内容は、相反するものであり、実際には設計パラメータである重み係数行列\(\boldsymbol{Q}\)と重み係数行列\(\boldsymbol{R}\)により、両者のトレードオフを図る(バランスを取る)ことが必要となります。
LQ制御理論によれば、この評価関数\(\boldsymbol{J}\)を最小にする制御量\(\boldsymbol{u}\)は、次のように定式化されています。
$$\boldsymbol{u} = \; – \boldsymbol{R}^{-1} \boldsymbol{b}^T \boldsymbol{P} \boldsymbol{X} = \; – \boldsymbol{K} _g \boldsymbol{X} \tag{式-8}$$
ただし、\(\boldsymbol{P}\)は、次式のリカッチ方程式の解です。
このリカッチ方程式を解くことにより、状態フィードバックゲインを求めることができます。
(式-3)に(式-8)を代入した次式で表される閉ループシステムは、最適レギュレータと呼ばれています。
$$\dot{\boldsymbol{X}} = ( \boldsymbol{A} \; – \boldsymbol{B} \boldsymbol{K}_g ) \boldsymbol{X} + \boldsymbol{E} \boldsymbol{w} \tag{式-10}$$
最適レギュレータは漸近安定、つまり、次式の行列は安定行列となり、その固有値も自動的に決定されます。
$$\boldsymbol{A}^0 = \boldsymbol{A} \; – \boldsymbol{B} \boldsymbol{K}_g \tag{式-11}$$
アクティブ動吸振器による平行板バネ構造物の制御系設計
制振対象は下図に示す平行板ばね構造物とし、「振動モード形を利用したモデリング入門」によりモデルを作成し、アクティブ動吸振器により、制振対象の1次と2次の振動モードを制御します。
アクティブ動吸振器は、下図の質点M1の上に設置しています。
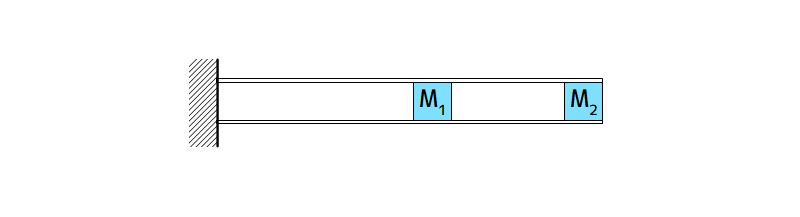
平行板ばね構造物
図1 平行板ばね構造物
ここでは、運動方程式を状態方程式表示した後、一般的な解析結果を得るために、無次元化状態方程式を導入します。
制御力の調整(制振効果をどの程度にするか)については、無次元系と次元系の相似則を明らかにした後、根軌跡図を利用した制御系設計法を説明します。
制御対象の運動方程式と状態方程式
下図に、制振対象とアクティブ動吸振器を含めた力学モデルを示します。

制振対象とアクティブ動吸振器の力学モデル
図2 制振対象とアクティブ動吸振器の力学モデル
ここで、相対変位を次のように定義します。
$$\boldsymbol{X}_c = \boldsymbol{X}_d \; – \boldsymbol{X}_1 \tag{式-12}$$
この相対変位を用いると上図の力学モデルの運動方程式は、以下のようになります。
$$\ddot{\boldsymbol{X}_2} = \frac{\boldsymbol{K}_2}{\boldsymbol{M}_2} \boldsymbol{X}_1 \; – \frac{\boldsymbol{K}_2}{\boldsymbol{M}_2} \boldsymbol{X}_2 \tag{式-14}$$
状態変数ベクトルを次のように定義すると、
$$\boldsymbol{X} = \begin{Bmatrix} \; \dot{X_1} \; \dot{X_2} \; \dot{X_c} \; X_1 \; X_2 \; X_c \end{Bmatrix}^T \tag{式-16}$$
状態方程式は、次式で表されます。
$$\dot{\boldsymbol{X}} = \boldsymbol{A} \boldsymbol{X} + \boldsymbol{b} \boldsymbol{u} \tag{式-17}$$
ただし、
\(\boldsymbol{A} = \begin{bmatrix} 0 & 0 & 0 & – \frac{K_1+K_2}{M_1} & \frac{K_2}{M_1} & \frac{k}{M_1} \\ 0 & 0 & 0 & \frac{K_2}{M_2} & – \frac{K_2}{M_2} & 0 \\ 0 & 0 & 0 & \frac{K_1+K_2}{M_1} & – \frac{K_2}{M_1} & – \left( \frac{k}{M_1} + \frac{k}{m} \right) \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \end{bmatrix}\)
\(\boldsymbol{b} = K_c \cdotp \begin{bmatrix} \frac{1}{M_1} & 0 & – \left( \frac{1}{M_1} + \frac{1}{m} \right) & 0 & 0 & 0 \end{bmatrix}^T\)
\(K_c\):制御力と制御量との関係を示す力変換係数
状態方程式の無次元化
一般性のある制御系設計資料を得るため、状態方程式を無次元化します。
まず、次の無次元量、及び、スケール変換係数を導入します。
\(\Omega_1\)、\(\Omega_2\)、\(\omega\)は、各々質点1、質点2、アクティブ動吸振器の固有振動数です。
$$\Omega_1 = \sqrt{K_1 / M_1} $$
$$\Omega_2 = \sqrt{K_2 / M_2} $$
$$\omega = \sqrt{k / m} $$
$$\mu = m / M_1 $$
$$\mu_c = M_2 / M_1 $$
$$\gamma_1 = \omega / \Omega_1 $$
$$\gamma_2 = \Omega_2 / \Omega_1 $$
$$\ddot{X}_1 = {\Omega_1}^2 \bar{\ddot{X}}_1 $$
$$\dot{X}_1 = {\Omega_1} \bar{\dot{X}}_1 $$
$$X_1 = \bar{X}_1 $$
$$\ddot{X}_2 = {\Omega_1}^2 \bar{\ddot{X}}_2 $$
$$\dot{X}_2 = {\Omega_1} \bar{\dot{X}}_2 $$
$$X_2 = \bar{X}_2 $$
$$\ddot{X}_c = {\Omega_1}^2 \bar{\ddot{X}}_c $$
$$\dot{X}_c = {\Omega_1} \bar{\dot{X}}_c $$
$$X_c = \bar{X}_c $$
$$k_i = \frac{M_1 \Omega_1}{K_c} \bar{k}_i \quad ( i = 1, 2, 3 ) $$
$$k_j = \frac{M_1 {\Omega_1}^2}{K_c} \bar{k}_j \quad ( j = 4, 5, 6 ) $$
$$u = \frac{M_1 {\Omega_1}^2}{K_c} \bar{u} $$
ここで、状態変数ベクトルを次のように定義します。
$$\bar{\boldsymbol{X}} = \begin{Bmatrix} \; \bar{\dot{X}_1} \; \bar{\dot{X}_2} \; \bar{\dot{X}_c} \; \bar{X}_1 \; \bar{X}_2 \; \bar{X}_c \end{Bmatrix}^T \tag{式-18}$$
これらの係数を用いると、無次元化状態方程式は、次式で表されます。
$$\bar{\dot{\boldsymbol{X}}} = \bar{\boldsymbol{A}} \bar{\boldsymbol{X}} + \bar{\boldsymbol{b}} \bar{\boldsymbol{u}} \tag{式-19}$$
ただし、
\(\boldsymbol{A} = \begin{bmatrix} 0 & 0 & 0 & – ( 1 + \mu_c {\gamma_2}^2 ) & \mu_c {\gamma_2}^2 & \mu {\gamma_2}^2 \\ 0 & 0 & 0 & {\gamma_2}^2 & – {\gamma_2}^2 & 0 \\ 0 & 0 & 0 & 1 + \mu_c {\gamma_2}^2 & – \mu_c {\gamma_2}^2 & – {\gamma_1}^2 ( 1 + \mu ) \\ 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 0 & 0 & 0 \end{bmatrix}\)
\(\bar{\boldsymbol{b}} = \begin{bmatrix} 1 & 0 & – \left( 1 + \frac{1}{\mu} \right) & 0 & 0 & 0 \end{bmatrix}^T\)
LQ制御理論による制御系設計
制御系設計には、上述のLQ制御理論を用います。
ここでの設計パラメータは、次式で表される線形2次形式の評価関数\(\boldsymbol{J}\)に与える重み係数行列\(\boldsymbol{Q}\)と重み係数\(R\)になります。
$$\boldsymbol{J} = \int_0^\infty ( \boldsymbol{X}^T \boldsymbol{Q} \boldsymbol{X} + u^2 R ) \; dt \tag{式-20}$$
ただし、
\(\boldsymbol{Q} = diag \; \left[ \; q_1, q_2, q_3, q_4, q_5, q_6 \right]\)
ここで、
\(q_1\):質点1の速度に掛かる重み係数
\(q_2\):質点2の速度に掛かる重み係数
\(q_3\):相対速度に掛かる重み係数
\(q_4\):質点1の変位に掛かる重み係数
\(q_5\):質点1の変位に掛かる重み係数
\(q_6\):相対変位に掛かる重み係数
LQ制御理論によれば、この評価関数\(\boldsymbol{J}\)を最小にする制御量\(u\)は、次のように定式化されています。
$$u = \; – R^{-1} \boldsymbol{b}^T \boldsymbol{P} \boldsymbol{X} = \; – \boldsymbol{K} _g \boldsymbol{X} \tag{式-21}$$
ただし、
$$\boldsymbol{K} = \begin{Bmatrix} k_1, k_2, k_3, k_4, k_5, k_6 \end{Bmatrix} $$
ここに、\(\boldsymbol{P}\)は、次式のリカッチ方程式の解です。
このリカッチ方程式を解くことにより、状態フィードバックゲインを求めることができます。
ところが、設計パラメータである重み係数行列\(\boldsymbol{Q}\)と重み係数\(R\)の値と得られる制御系の特性との関係が不明であるため、試行錯誤的に設計パラメータを決定し、制御系を設計しているのが現状です。
無次元化状態方程式による制御系設計
解析結果に一般性を持たせるため、無次元化状態方程式を用い、無次元系の重み行列を次式とします。
$$\bar{\boldsymbol{Q}} = diag \; \left[ \; \bar{q}_1, \bar{q}_2, \bar{q}_3, \bar{q}_4, \bar{q}_5, \bar{q}_6 \right]$$
制御量は、次式となります。
$$\bar{u} = \; – \bar{\boldsymbol{K}} \bar{\boldsymbol{X}} \tag{式-23}$$
ただし、
\(\bar{\boldsymbol{K}} = \begin{Bmatrix} \bar{k}_1, \bar{k}_2, \bar{k}_3, \bar{k}_4, \bar{k}_5, \bar{k}_6 \end{Bmatrix} \)
無次元系の状態フィードバックゲインは、無次元系のリカッチ方程式を解くことにより求めることができます。
次元系と無次元系との相似則
LQ制御理論による無次元系と次元系の状態フィードバックゲイン\(\boldsymbol{K}\)、重み係数行列\(\boldsymbol{Q}\)、及び、重み係数\(\boldsymbol{R}\)には、次式の相似則が成立します。
$$\boldsymbol{K} = \frac{M_1 {\Omega_1}^2}{K_c} \left[ \frac{\bar{k}_1}{\Omega_1} \; \frac{\bar{k}_2}{\Omega_1} \; \frac{\bar{k}_3}{\Omega_1} \; \bar{k}_4 \; \bar{k}_5 \; \bar{k}_6 \right] \tag{式-24}$$
$$\boldsymbol{R} = { \left( \frac{K_c}{M_1 {\Omega_1}^2} \right) }^2 \; \bar{\boldsymbol{R}} \; \tag{式-26}$$
したがって、無次元系のリカッチ方程式を解いて、\(\bar{k}_1\)~を\(\bar{k}_6\)決めて、制御系を設計することができます。
また、無次元系で得られた解析結果は、次元系にもそのまま適用することができます。
制振効果の解析
重み係数による制振効果の違いについて、根軌跡図、周波数応答(伝達関数)、及び、シミュレーション(インパルス応答、時間応答)により確認します。
根軌跡図による重み係数による制振効果の比較
無次元系の重み係数行列\(\boldsymbol{Q}\)と重み係数\(R\)の値と得られる制御系の特性との関係を明らかにするため、根軌跡図を利用します。
図3は質点1と2の変位項に、図4は質点1と2の速度項に重みを掛け、重み係数\(R\)を小さくした(制御を強くしていった)場合の無次元系の根軌跡図です。
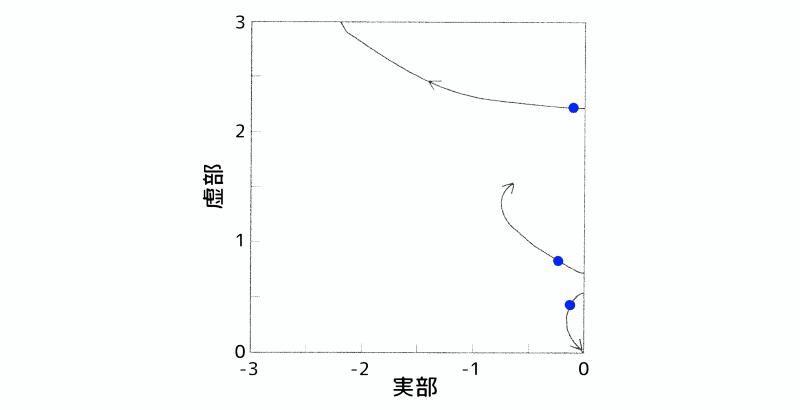
根軌跡図:質点1と質点2の変位項に重みを掛けた場合
図3 根軌跡図:質点1と質点2の変位項に重みを掛けた場合
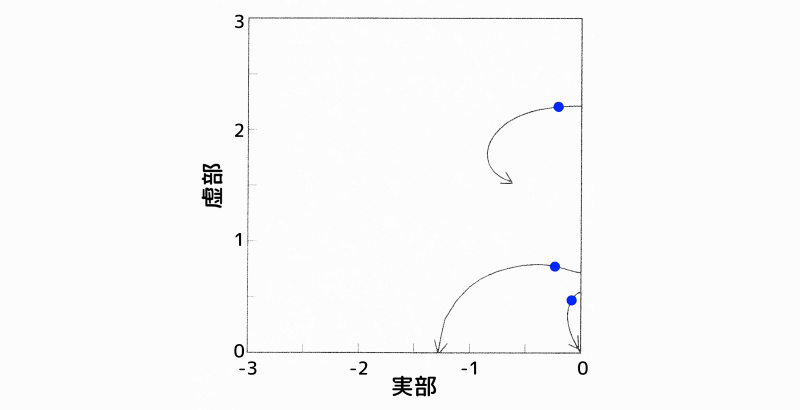
根軌跡図:質点1と質点2の速度項に重みを掛けた場合
図4 根軌跡図:質点1と質点2の速度項に重みを掛けた場合
この制御系においては、3個の特性根が存在します。原点に近い根から、アクティブ動吸振器、制振対象の1次、2次の根になります。
また、根軌跡図において、根と実軸とがなす角度は減衰の程度を示しています。つまり、根が実軸から離れるほど制振効果が高くなるということです。
なお、変位項と速度項の制振効果の比較のため、根軌跡図に\(\bar{R}=10\)の点を青丸でプロットしています。
図3と図4から、以下の事が分かります。
(1)変位項に重みを掛けた場合
- アクティブ動吸振器の根と制振対象の1次の根は互いに反発し、アクティブ動吸振器の根は原点に収束します。
- 制振対象の1次と2次の根は、当初接近します。その後1次の根はS平面の1点に収束し、2次の根はさらにS平面を左に移動します。
(2)速度項に重みを掛けた場合
- アクティブ動吸振器の根は、原点に収束します。
- 制振対象の1次と2次の根は、当初接近します。1次の根は実軸上に引き込まれ、2次の根はS平面の1点に収束します。
(3)制振効果の比較
図3と図4の青丸は、それぞれ変位項、速度項に重みを掛け、重み係数を\(\bar{R}=10\)とした場合の根です。
- アクティブ動吸振器の根と制振対象の1次の根は、虚軸からほとんど同一の点にあります。
- 制振対象の2次の根は、速度項に重みを掛けた場合の方が虚軸より左に位置しています。
従って、速度項の方が、変位項よりも2次のピークをより大きく安定化する効果があると考えることができます。
伝達関数による重み係数による制振効果の比較
変位項と速度項の制振効果を周波数応答(伝達関数)により比較します。
下図に、重み係数による周波数応答の比較を示します。
上図において、点線が非制御時、細線が変位項に重みを掛けた場合、太線が速度項に重みを掛けた場合の周波数応答(伝達関数)です。
同図より、根軌跡図での解析と同様、速度項に重みを掛けた場合のほうが、2次モードの安定化効果が高いことが分かります。
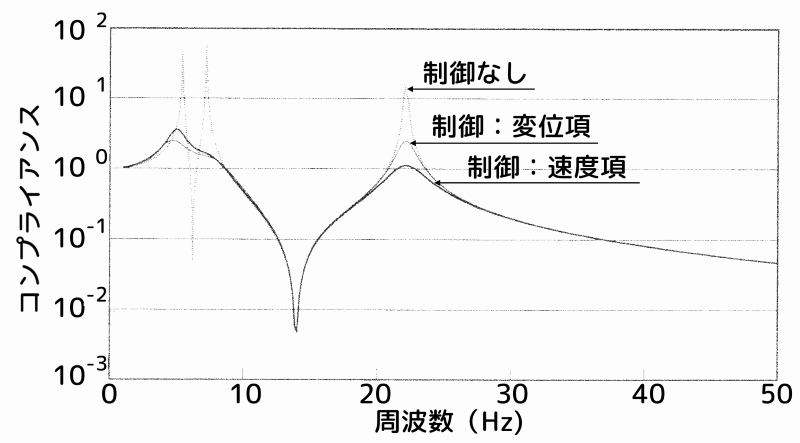
重み係数による周波数応答の比較
図5 重み係数による周波数応答の比較
これまでの結果から、2次のピークを安定化させたい場合には、速度項に重みを掛けた方が、変位項に重みを掛けた場合よりも制振効果が高いことが分かります。
この様に、重み係数に応じた根軌跡図を作成することにより、重み係数と得られる制御系の特性との関係を明らかにすることができます。
インパルス応答による重み係数による制振効果の比較
下図に、変位項に重みを掛けた場合のインパルス応答(時間応答)を示します。
上図の上側が質点1、下側が質点2のインパルス応答です。
細線が非制御時、太線が制御時の応答です。
制御により、速やかに振動が収束していることが分かります。
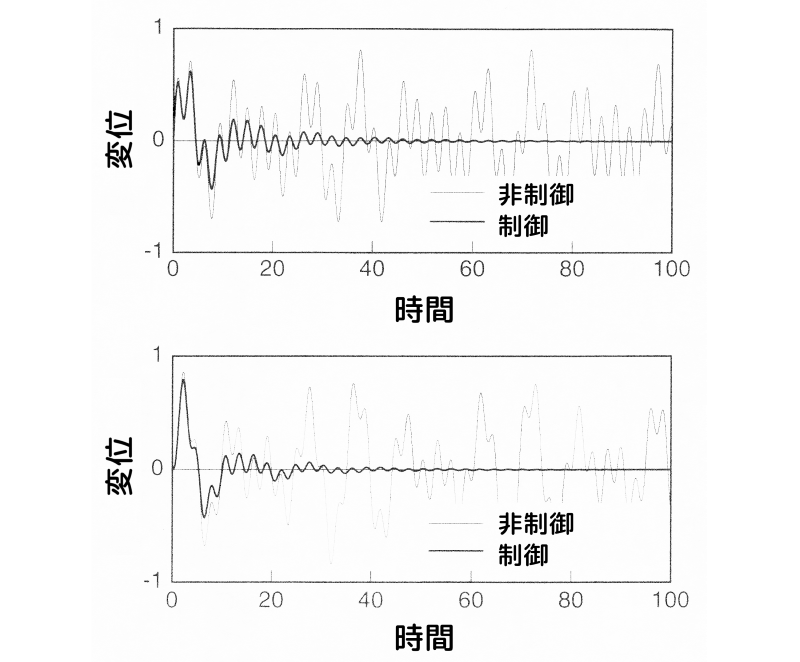
変位項に重みを掛けた場合のインパルス応答
図6 変位項に重みを掛けた場合のインパルス応答
下図に、速度項に重みを掛けた場合の時間応答(インパルス応答)を示します。
上図の上側が質点1、下側が質点2のインパルス応答です。
細線が非制御時、太線が制御時の応答です。
制御により、速やかに振動が収束していることが分かります。
また、図6の変位項に重みを掛けた場合と比較すると、速度項に重みを掛けた場合の方が、2次の振動がより早く収束していることが分かります。
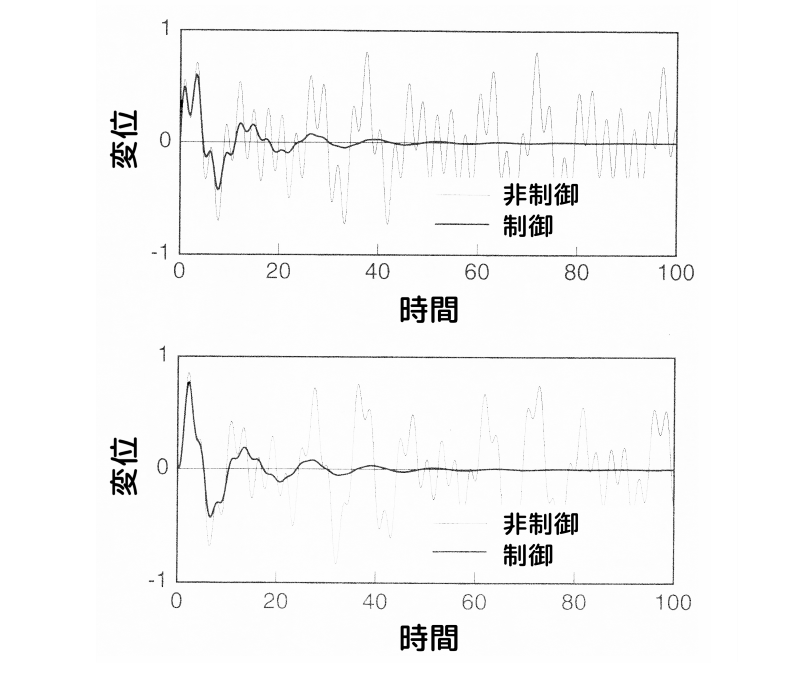
速度項に重みを掛けた場合のインパルス応答
図7 速度項に重みを掛けた場合のインパルス応答
まとめ
ここでは、現代制御理論の1つであるLQ最適制御について、一般的な数値解析結果を得るため、無次元化状態方程式を使った制御系設計方法について説明しました。
制振対象は平行板ばね構造物とし、アクティブ動吸振器により、制振対象の1次と2次の振動モードを制御を例に、以下の項目について説明しました。
- 現代制御理論のメリットと課題
- 運動方程式と振動制御系
- LQ制御理論
- アクティブ動吸振器による平行板バネ構造物の制御系設計
- 制御対象の運動方程式と状態方程式
- 状態方程式の無次元化
- LQ制御理論による制御系設計
- 無次元化状態方程式による制御系設計
- 次元系と無次元系との相似則
- 制振効果の解析
- 根軌跡図による重み係数による制振効果の比較
- 伝達関数による重み係数による制振効果の比較
- インパルス応答による重み係数による制振効果の比較


