「振動は難しいもの」というイメージの方は少なくないようですが、「身近にある振動・騒音について」で説明しているように、意外に知らないだけで身近にあるのも振動です。
ここでは、振動は初めてという方を想定して、ばねの振動を例に、振動の種類(自由振動、固有振動、減衰振動)について説明します。
振動とはどの様なもので、どんな風に表すことができるのかのイメージが伝われば幸いです。
ばねの振動
ここでは、ばねの振動について、下図の様にコイルばねの一端を固定し(吊り下げ)、他端に重りを着けたモデルで説明します。
ここでは、力学的な意味合いではなく、ばねを引っ張ることで重りが動く(振動する)現象についてのイメージが伝わればよいと考えています。
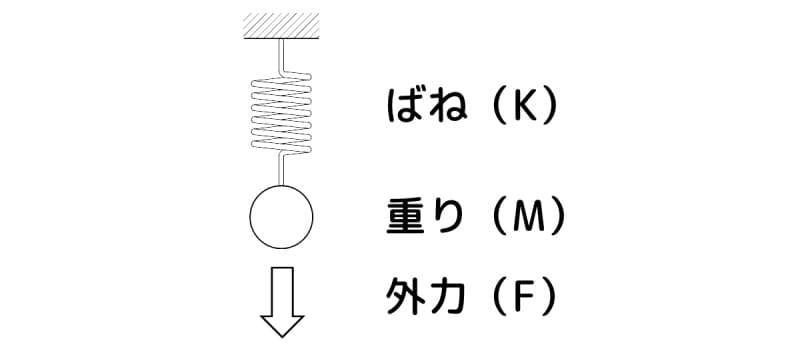
ばねと重りのモデル
図1 ばねと重りのモデル
上図において、力(外力)を加えないと重りは静止します。(ばねの力(復元力)と重り(重力)とがつりあっているということです。)
この静止した状態で、重りを下方に引っ張って離すと、ばねは動き始めます。これを自由振動と言います。
このばねの振動による、重りの位置を図示すると下図の様になります。
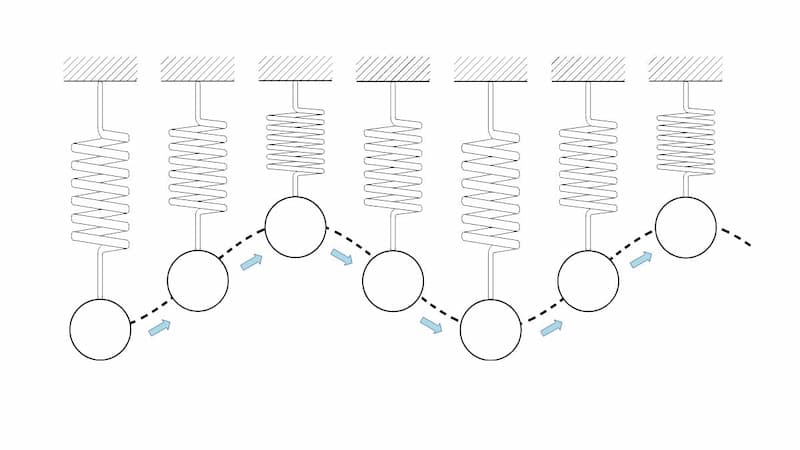
ばねの振動:自由振動
図2 ばねの振動:自由振動
やがて、ばねは一定の周期(固有振動数)で振動するようになります。これを固有振動と呼びます。
さらに、振動しているばねに外力を全く加えずにおくと、次第に重りの振動(上下動)が小さくなり、やがて静止します。
これは、実際のばねや重りが空気中を振動すると、ばねや重りと空気との間に摩擦が生じるため、ばねの振動が減衰していくためです。
ばねの振動に関係している力
外力を加えない場合、ばねと重りにかかる力はつりあい、静止しています。
ここでは、重りを引っ張ってばねを伸ばして外力を加え、手を離すことで振動(自由振動)している際のばねと重りにかかる力について説明します。
以下の説明では、図2を参考にしてください。
外力を加える前の静止した状態(平衡点)
外力が加えられていない状態(ばねと重りがつりあった状態)です。
- ばねには、重りにより引っ張られる力(復元力)が働いています。
- 重りには重力が働いています。

重力を考えるとさらに面倒になるので、以下の説明では無視してください。
外力を加える(重りを手で引っ張る)
重りが静止している状態(平衡点)から、重りを手で引っ張って外力を加えます。
- 伸びたばねには、ばねが元に戻ろうとする復元力が働きます。
外力を開放する(重りから手を放す)
手を離すとばねは振動を始めます。
- ばねは、外力により蓄えられた力(復元力)により縮み始めます。
- 重りは、ばねの復元力により動き始め、速度を増します。(慣性力により情報に移動し始める)
最下点から平衡点での力関係
ばねが振動しているとき、ばねの復元力と重りの慣性力は相互に影響しあっています。
- バネが伸びようとする力(復元力)は小さくなっていく。
- 重りの速度は慣性力により増していく。
平衡点での力関係
- ばねの復元力はゼロとなる。
- 重りは、慣性力により最大速度となります。
最上点での力関係
- 重りは静止し、最上点で速度の向きが反転します。
- バネの復元力は最大となります。(バネは伸びようとする)
最上点から平衡点での力関係
「最下点から平衡点」の場合とは力の向きが反転していますが、力や速度の関係は同様となります。
- バネが伸びようとする力(復元力)は小さくなっていく。
- 重りの速度は慣性力により増していく。
この後は、平衡点での力関係となり、上述の力関係が繰り返されます。

以上の説明をまとめると、「ばねの伸び縮みの力と重りの慣性力とが、相互に影響しあいながら振動している。」ということになります。
ばねの振動のモデル化とシミュレーション
ばねの振動が重りの空気抵抗などによりしだいに小さくなっていく現象は、ばねと重りのモデルを作成することでシミュレーションすることができます。
ここでは、詳細の説明はしませんが、下図は減衰振動の1例です。
- 縦軸が振幅(図1のばねと重りであれば、重りの位置)で、横軸は時間です。
- 黒の破線が減衰なしの場合、赤の実践は減衰を含む場合の振動を表しています。
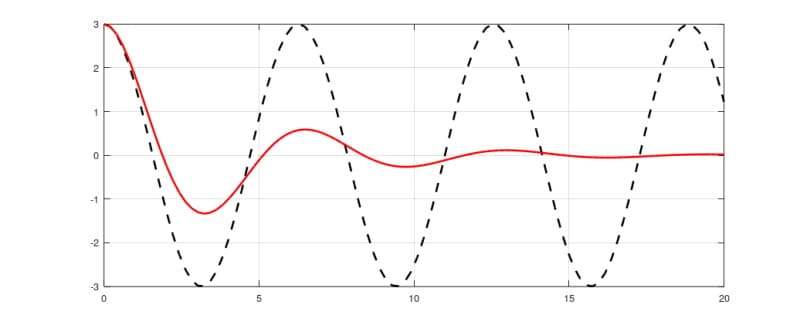
ばねの振動:減衰振動
図3 ばねの振動:減衰振動
例えば、一端を固定した板の振動は、ばね(ばね定数)、重り(質量)、ダンパー(減衰)から力学モデルを作ることでシミュレーションすることができます。
ばねと重りを力学モデルで表すと、簡略化していますが次式で表すことができます。
X=A・cos(ω・t)
ただし、
X:重りの位置
A:重りの振幅
ω:各振動数(rad/s)
t:時間
振動と力学モデルについては、別途まとめる予定です。
まとめ
「振動は難しいもの」と思われがちですが、意外に知らないだけで身近にあるのも振動です。
ここでは、ばねの振動を例に、振動の種類(自由振動、固有振動、減衰振動)について以下の項目で説明しました。
- ばねの振動
- ばねの振動に関係している力
- 外力を加える前の静止した状態(平衡点)
- 外力を加える(重りを手で引っ張る)
- 外力を開放する(重りから手を放す)
- 最下点から平衡点での力関係
- 平衡点での力関係
- 最上点での力関係
- 最上点から平衡点での力関係
- ばねの振動のモデル化とシミュレーション