バットのハンマリング試験で始めるモード解析入門では、実際に計測したデータから簡易的な振動モード形を作成しています。

これまで何度もやってきたバットのハンマリングと振動モード形作成ですが、振動モード形に違和感を感じ思わぬミスをしていたことに気づいたことがあります。
ここでは、ハンマリング試験と振動モード形作成時の思わぬミスについてまとめています。
バットのハンマリング試験による伝達関数の計測での失敗談
ここでは、バットのハンマリング試験の計測データから簡易的な振動モード形を作成した際に、

計測データに間違いはないのだが、振動モード形状がおかしい。
ことに気づいたものの何度計測しても結果が変わらず悩んだことがあります。
理由が分かれば簡単なことで、
- 周波数応答関数の縦軸がログスケール(対数表示)になっていた
ことにより、
- バットの1次モードの振動モード形の両端の形状がおかしい。
- 特に両端の周波数応答関数の値が小さい。
結果となっていました。
振動モード形は、ある周波数(固有振動数)での各点の振幅と位相の情報を利用するので、振幅を対数で扱うとおかしなことになります。
何かがおかしいことに気づきながら、原因に気づくまで時間がかかりましたので、バットの振動モード形を周波数応答関数データから簡易的に作成する場合にどうなったのかについて説明します。
バットの計測点と周波数応答関数の例
詳細は省きますが、計測対象であるバットの計測点を下図に示します。
計測点は5か所、センサは計測点1の反対側に設置します。
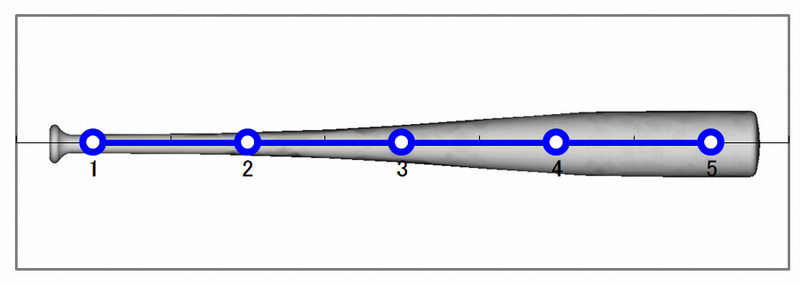
バットの計測点
図1 バットの計測点
下図は、周波数応答のゲイン(アクセレランス)、位相の計測データの一例です。
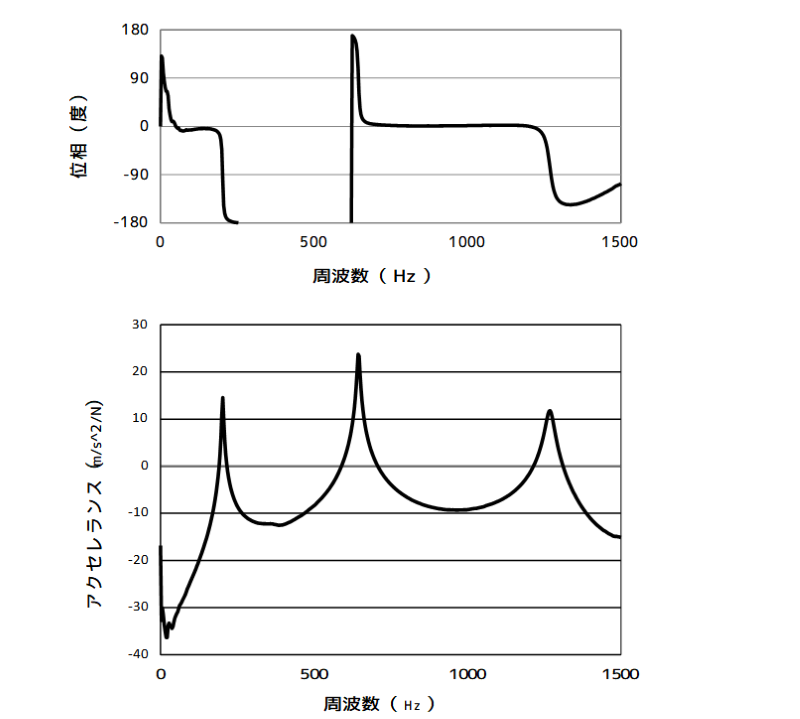
周波数応答関数のデータ例
図2 周波数応答関数(伝達化数)のデータ例
上図の周波数応答関数のアクセレランスの縦軸がリニア表示であることに注意してください。
簡易的な振動モード形状の作成:正解
まずは、正しいデータ処理から振動モード形を作成した例について説明します。
ゲイン(振動の大きさ)及び位相(振動の向き)データ整理
計測した周波数応答関数から、以下の表を作成します。
バットの1次から3次モードの共振周波数における周波数応答関数の大きさ(ゲイン)の値と位相(プラスかマイナスか)を記入します。
| 計測点 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1次モード | 43 | 33 | 39 | 25 | 35 |
| 位相 | + | - | - | - | + |
| 2次モード | 35 | 44 | 34 | 34 | 34 |
| 位相 | + | - | + | + | - |
| 3次モード | 11 | 9 | 15 | 15 | 13 |
| 位相 | - | - | + | - | + |
表1 1次~3次モードの周波数応答関数と位相データ
振動モード形の作成
表計算ソフトを使ったバットの振動モード形の作図例を以下に示します。
ここでは、表計算ソフトで、周波数応答関数のアクセレランスの絶対値が最大値を1として正規化しています。
上からバットの1次、2次、3次モードです。
計測点を増やすとより滑らかな振動モード形を得ることができます。
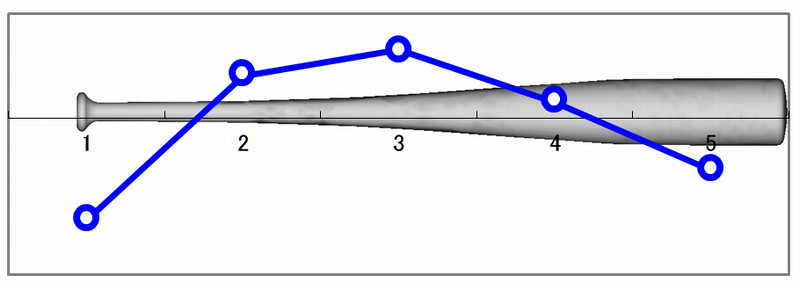
バットの1次モード
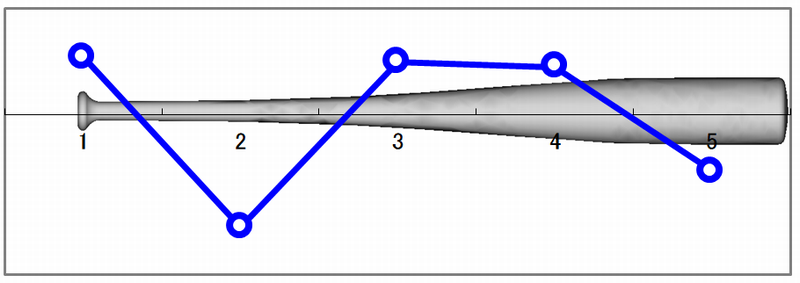
バットの2次モード
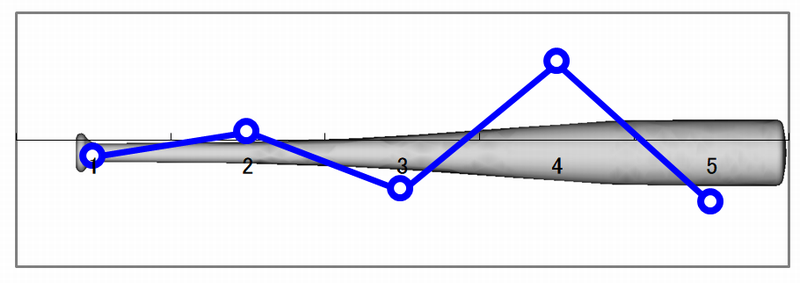
バットの3次モード
図3 表計算ソフトを使った振動モード形の作図例
簡易的な振動モード形状の作成:ミスした経験から
ここでは、周波数応答関数のデータをLog表示(対数表示)でyとみとった場合について説明します。
ゲイン(振動の大きさ)及び位相(振動の向き)データ整理
計測したLog表示(対数表示)周波数応答関数のデータは、以下の表となります。
計測点が5点と少ないので、バットの1次モードの共振周波数における周波数応答関数の大きさ(ゲイン)の値と位相(プラスかマイナスか)になります。
| 計測点 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1次モード | 1.6 | 1.2 | 1.4 | 0.8 | 1.3 |
| 位相 | + | - | - | - | + |
表2 1次モードの周波数応答関数(Log表示)と位相データ
振動モード形の作成
表計算ソフトを使ったバットの1次の振動モード形の作図例を以下に示します。
青線がLin表示、赤線がLog表示(対数表示)のデータを使って作成した振動モード形です。
ここでは、表計算ソフトで、青線の最大値と赤線の最大値を1として正規化しています。
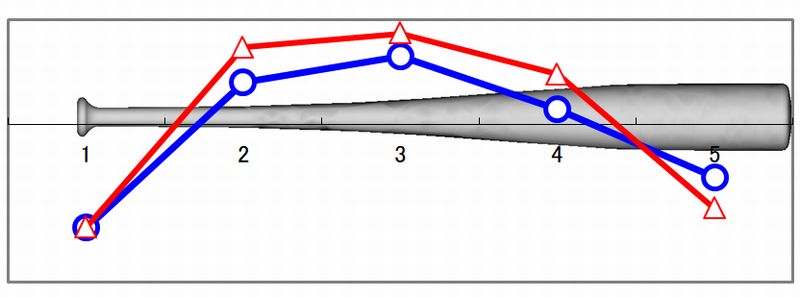
振動モード形の作図例(Lin表示とLog表示データの比較)
図4 振動モード形の作図例(Lin表示とLog表示データの比較)
Lin表示とLog表示のデータとでは、全体的な振動モード形状は似たように見えますが、
- バットの形状が均一ではない。
- グリップ部分が細く、ヘッドの部分が太い。
にもかかわらず、赤線(Log表示)の振動モード形では、
- 棒の振動モード形状に近い形状となっている。
ため、何か変だと感じたのでした。

単位の確認は重要です。
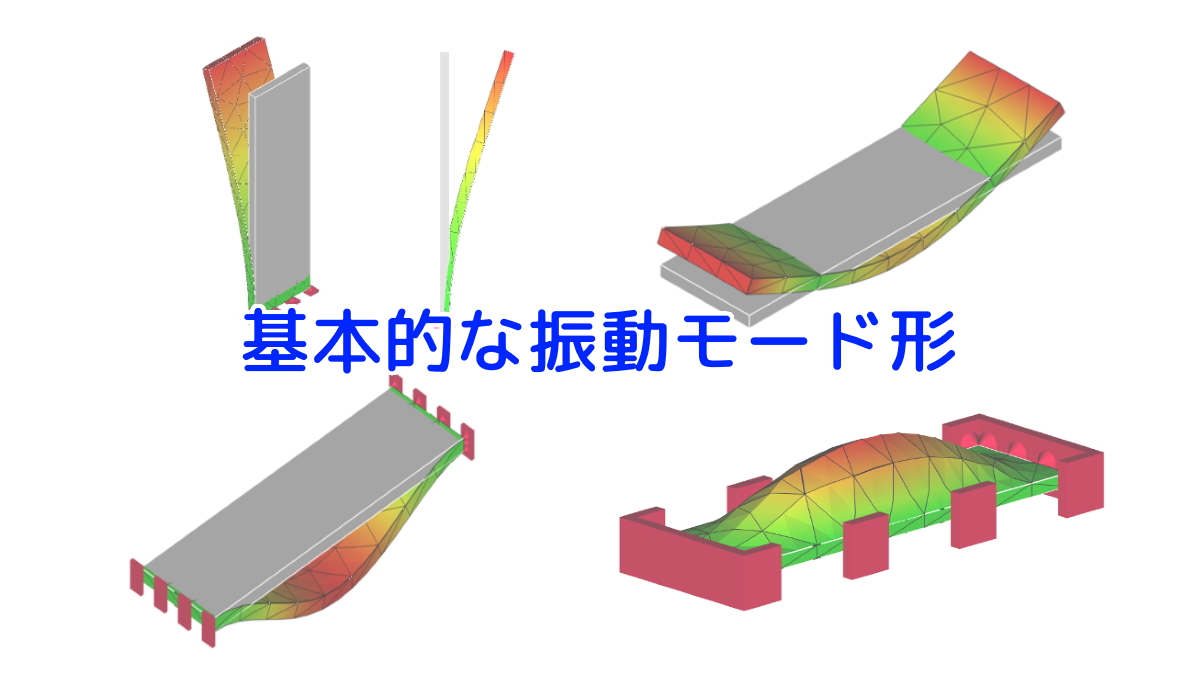
基本的な振動モード形状については、FEMの固有値解析結果を利用して理解を深めておくと、実験モード解析で振動モード形について考察する際に役立ちます。

まとめ
これまで何度もやってきたバットのハンマリングと振動モード形作成ですが、振動モード形に違和感を感じ思わぬミスをしていたことに気づいたことがあります。
計測時の周波数応答関数(伝達関数)のグラフ表示の誤りが原因でした。
ここでは、以下の項目で説明しました。
- バットのハンマリング試験による伝達関数の計測での失敗談
- バットの計測点と周波数応答関数の例
- 簡易的な振動モード形状の作成:正解
- ゲイン(振動の大きさ)及び位相(振動の向き)データ整理
- 振動モード形の作成
- 簡易的な振動モード形状の作成:間違い
- ゲイン(振動の大きさ)及び位相(振動の向き)データ整理
- 振動モード形の作成


