振動モード形については、振動モード形と計測点の選定については簡単に説明しました。
ここでは、基本的な振動モード形として、平板の固定なし(境界条件フリー)の場合の振動モード形状について説明します。
実験モード解析では、平板を吊ったり、スポンジ等にのせてハンマリング試験を行います。
【参考】計測対象物の支持方法
【参考】基本的な振動モード形
解析対象について
ここでは、140x40x5 mmのアルミニウム合金製の平板についてFreeCADの固有値解析を行い作成した振動モード形について説明します。
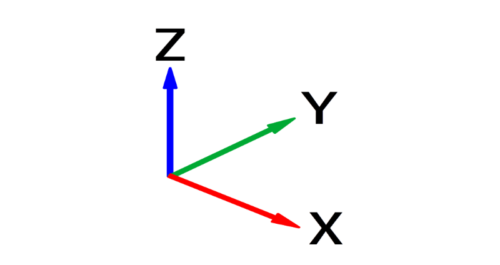
FEMの解析座標系の自由度と剛体モード
FEMの解析座標系における自由度は、下図に示すX、Y、Z軸の並進の3自由度に加え、各軸周りの回転3自由度の合計6自由度になります。
解析座標系
このため、ここで紹介しているように境界条件フリーの固有値解析では、1次から6次までの6個の振動モード形は、剛体モードと呼ばれ振動モードとしては意味のないモード形となります。
振動モード形の一覧
下表に、1辺を固定した平板の7次~20次までの振動モード形の一覧を示します。
1~6次の剛体モードは除いているため、7次モードが1次の振動モードを意味していますが、FreeCADの解析結果で得られるモード次数を使い説明します。
| モード次数 | モード形状(長手/短手方向) |
|---|---|
| 7 | 曲げ 1次 / 変形なし |
| 8 | ねじり 1次 |
| 9 | 曲げ 2次 / 変形なし |
| 10 | ねじり 2次 |
| 11 | 曲げ 3次 / 変形なし |
| 12 | 平面曲げ 1次 |
| 13 | ねじり 3次 |
| 14 | 曲げ 4次 / 変形なし |
| 15 | ねじり 4次 |
| 16 | 16次モード |
| 17 | 伸び縮み |
| 18 | 18次モード |
| 19 | 平面曲げ 2次 |
| 20 | 20次モード |
振動モード形
棒状のモノであれば、振動モード形状は線で表されるため、「振動モード形と計測点の選定」で説明した考え方で見ていきます。
平板の振動モード形の基本は、曲げモードです。
ここでは、平面の振動モード形を、平板の長手方向と短手方向からのモード形状の組み合わせとして見ていきます。
この他に共振周波数(固有振動数)で見ていくこともあります。
7次モード

7次モード
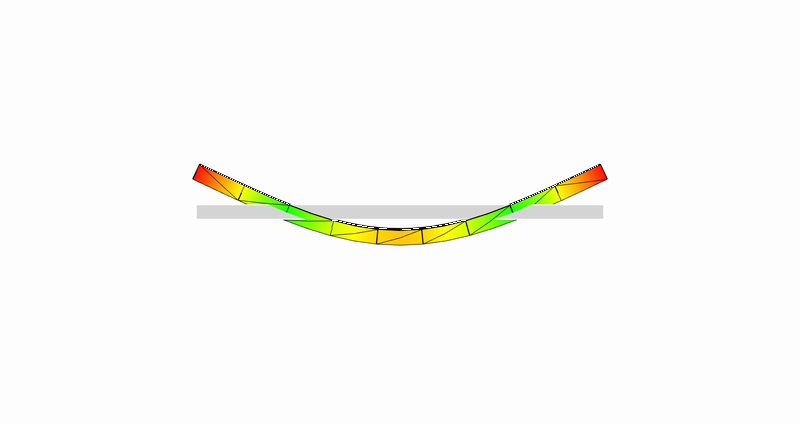
7次モード:長手方向
8次モード
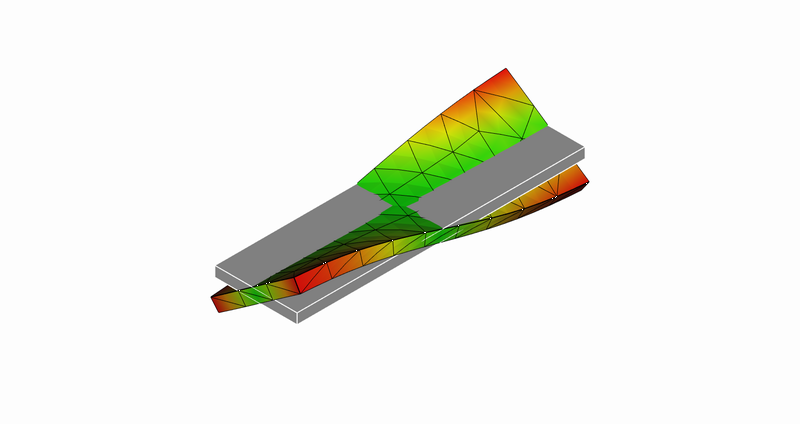
8次モード

8次モード:長手方向
9次モード

9次モード
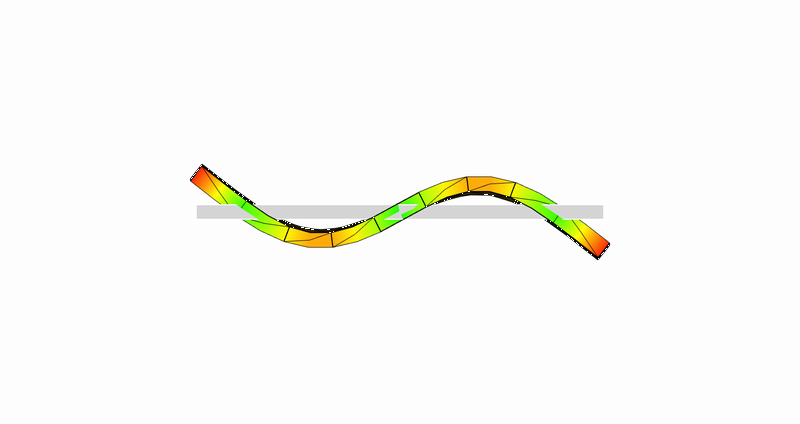
9次モード:長手方向
10次モード
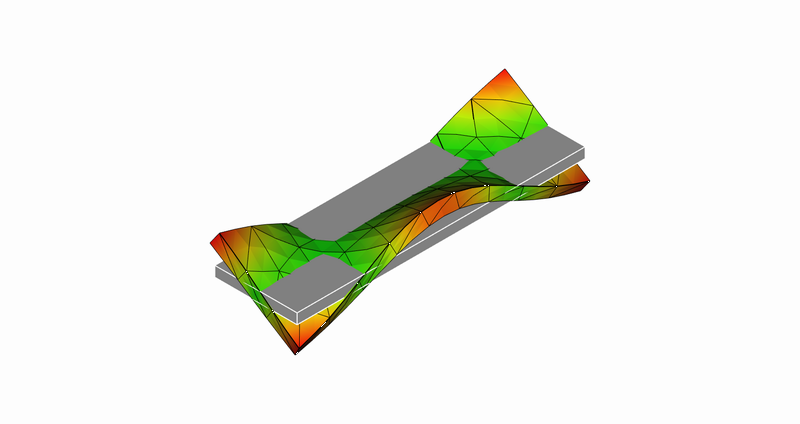
10次モード
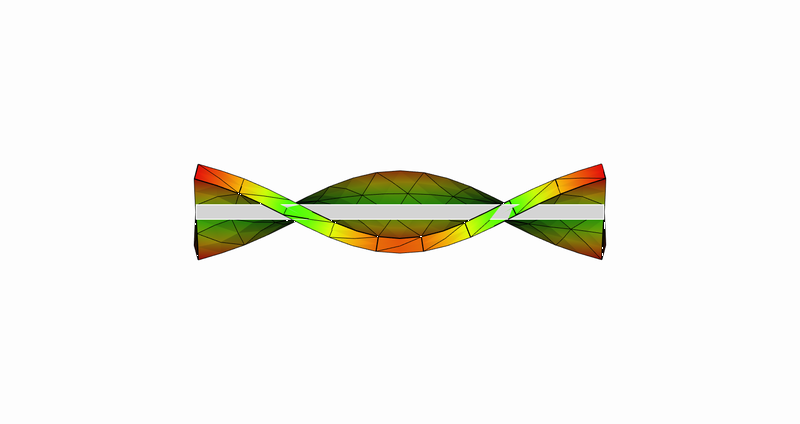
10次モード:長手方向
11次モード
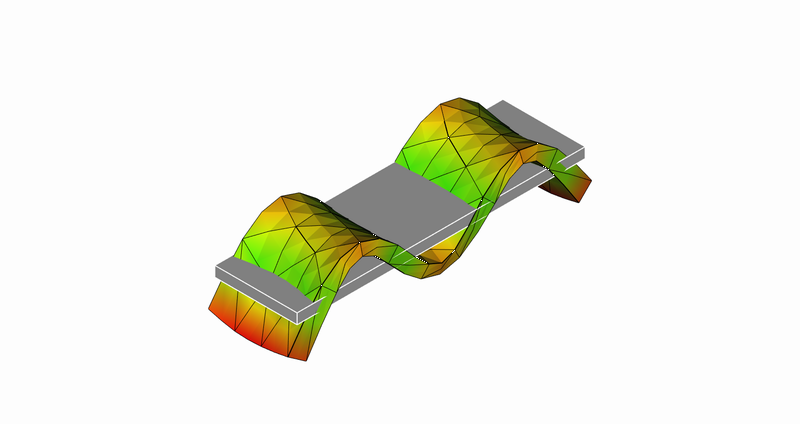
11次モード

11次モード:長手方向
12次モード
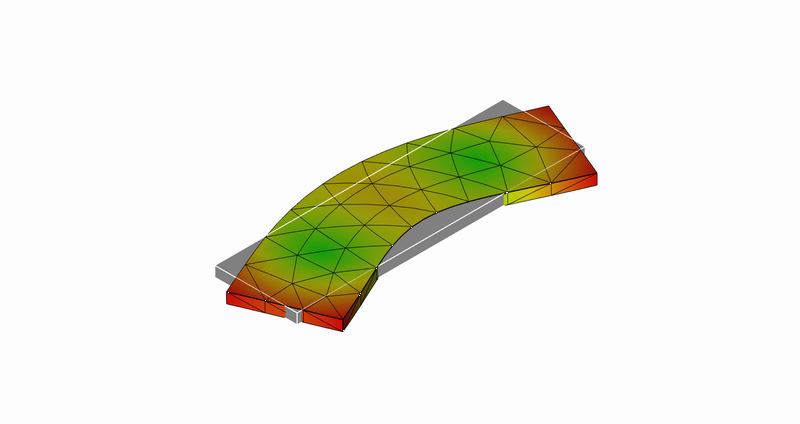
12次モード
13次モード
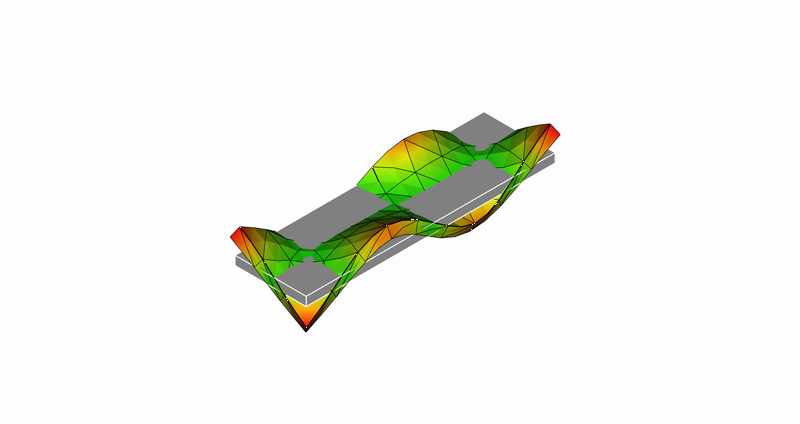
13次モード

13次モード:長手方向
14次モード
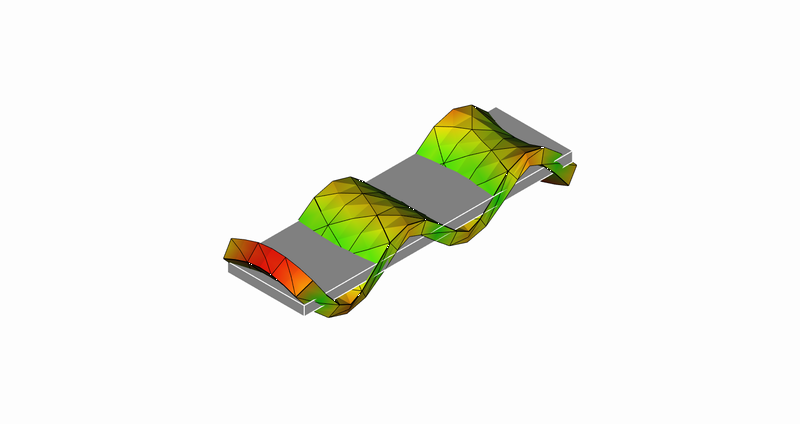
14次モード

14次モード:長手方向
15次モード
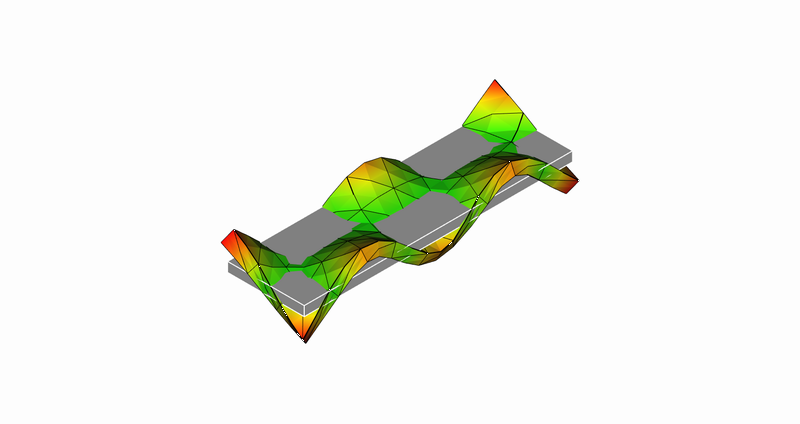
15次モード

15次モード:長手方向
16次モード
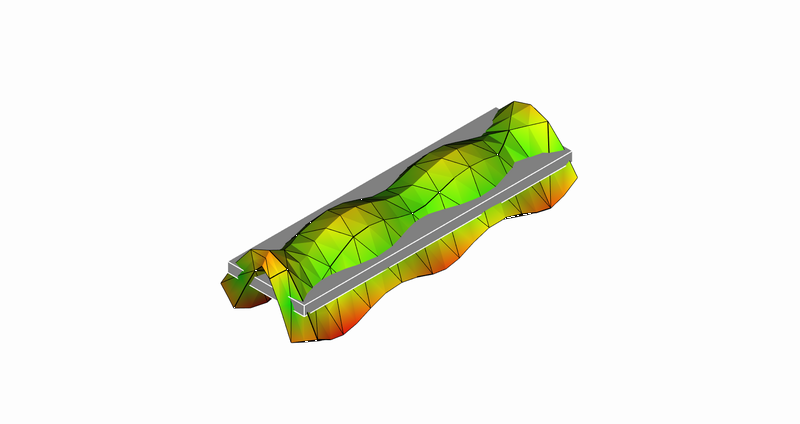
16次モード
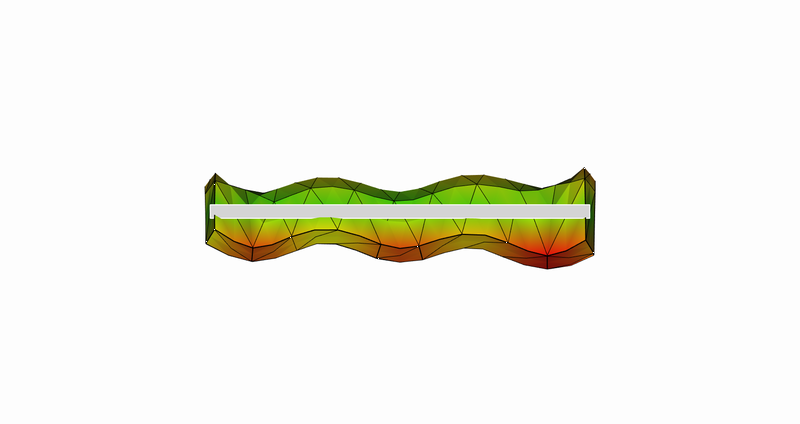
16次モード:長手方向
17次モード
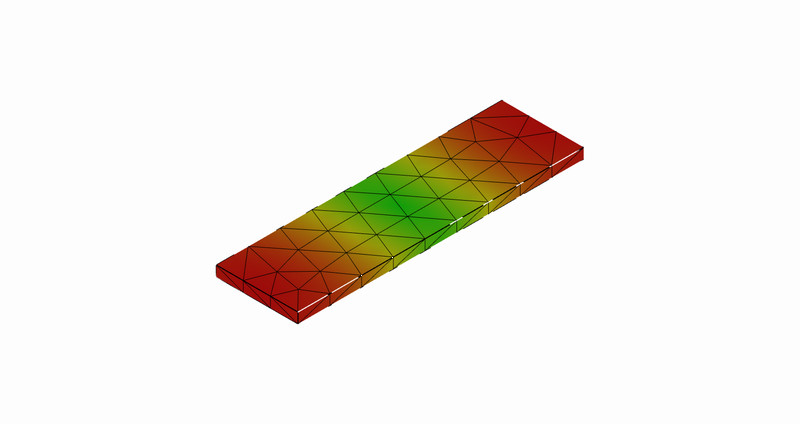
17次モード:伸び縮み
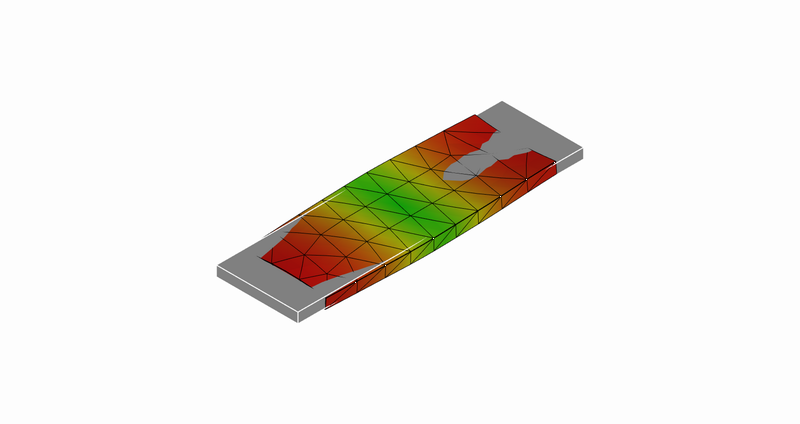
17次モード:伸び縮み
18次モード
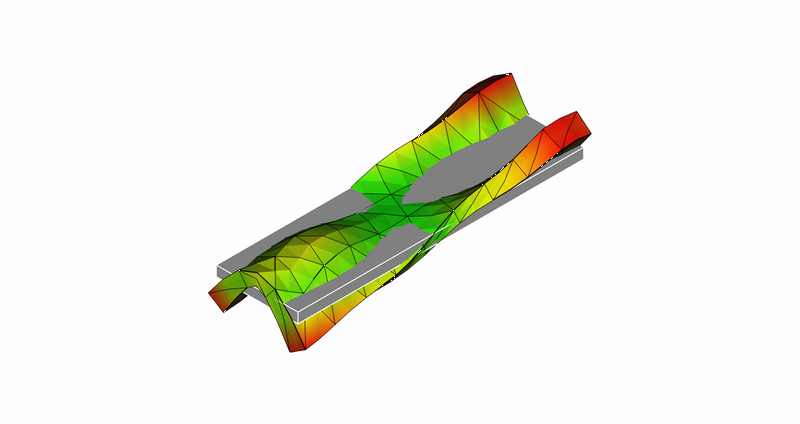
18次モード

18次モード:長手方向
19次モード
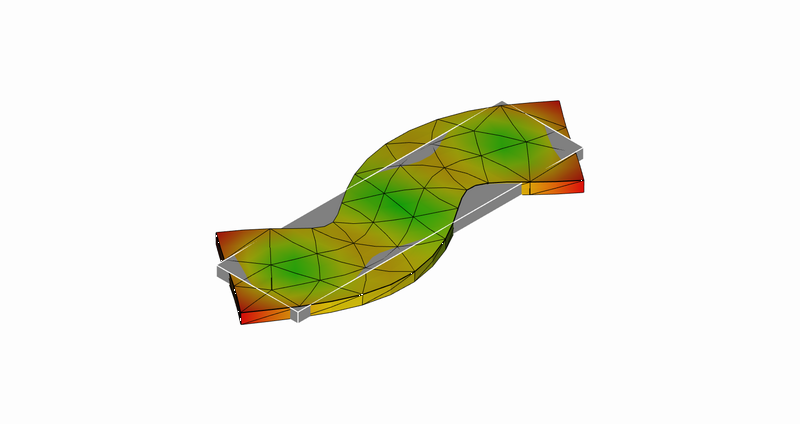
19次モード
20次モード
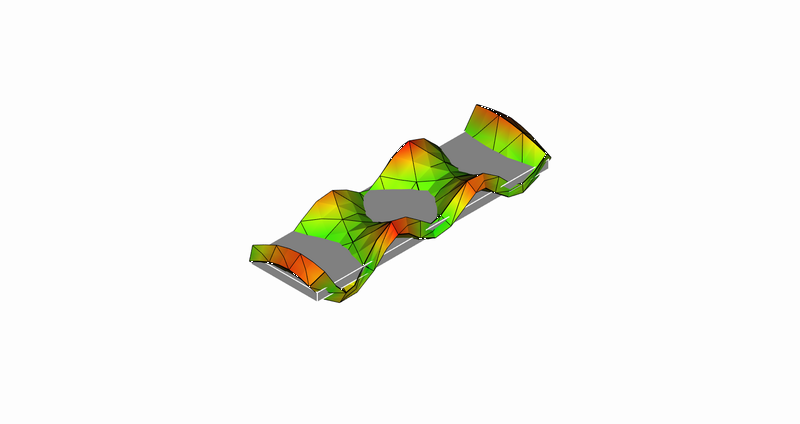
20次モード

20次モード:長手方向
まとめ
ここでは、基本的な振動モード形として、平板の固定なし(境界条件フリー)の場合の振動モード形状と剛体モードについて説明しました。