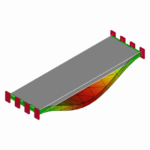
振動モード形については、振動モード形と計測点の選定については簡単に説明しました。
基本的な形状(棒や平板)について、拘束条件(自由、固定)による振動モード形状の違い、振動モードの腹と節との関係を知っておくことは、
- 実験モード解析とやFEMによる固有値解析との違いについての理解を深める
- 特定の振動モードを実験で確認するための計測点の選定
などにも有効です。
振動制御をする場合、「不可制御・不可観測性を活用した低次元化モデル作成」を利用して制振対象の低次元化モデルを作成する場合には、制振対象の振動モード形の節の位置を利用します。
ここでは、高層ビルや片持ち梁のような構造物の基本的な振動モード形として、平板の1辺を固定した場合の振動モード形状について説明します。
【参考】基本的な振動モード形
解析対象について
ここでは、140x40x5 mmのアルミニウム合金製の平板についてFreeCADの固有値解析を行い作成した振動モード形について説明します。
振動モード形の一覧
下表に、1辺を固定した平板の1次~10次までの振動モード形の一覧を示します。
| モード次数 | モード形状 |
|---|---|
| 1 | 曲げ 1次 |
| 2 | 曲げ 2次 |
| 3 | ねじり 1次 |
| 4 | 平面曲げ 1次 |
| 5 | 曲げ 3次 |
| 6 | ねじり 2次 |
| 7 | 曲げ 4次 |
| 8 | 平面曲げ 2次 |
| 9 | ねじり 3次 |
| 10 | 伸び縮み(長手方向) |
振動モード形
棒状のモノであれば、振動モード形状は線で表されるため、「振動モード形と計測点の選定」で説明した考え方で見ていきます。
平板の振動モード形の基本は、曲げモードです。
ここでは、平面の振動モード形を、平板の長手方向と短手方向からのモード形状の組み合わせとして見ていきます。
この他に共振周波数(固有振動数)で見ていくこともあります。
また、ハンマリング試験による実験モード解析の場合には、低い周波数から高い周波数までの周波数応答関数(伝達関数)のデータ計測が、使用するセンサーや検出できる信号レベル(大きさ)の影響により難しくなります。
このため特定の共振周波数(固有振動数)の計測を考慮したハンマリング試験を行うことがあります。
1次モード
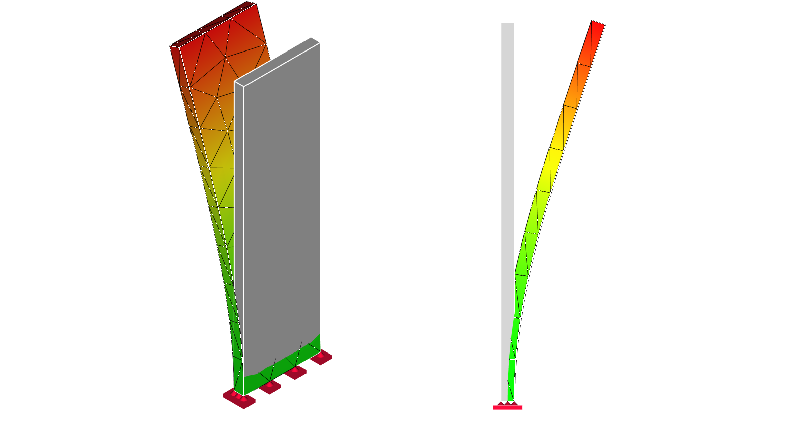
1次モード
2次モード
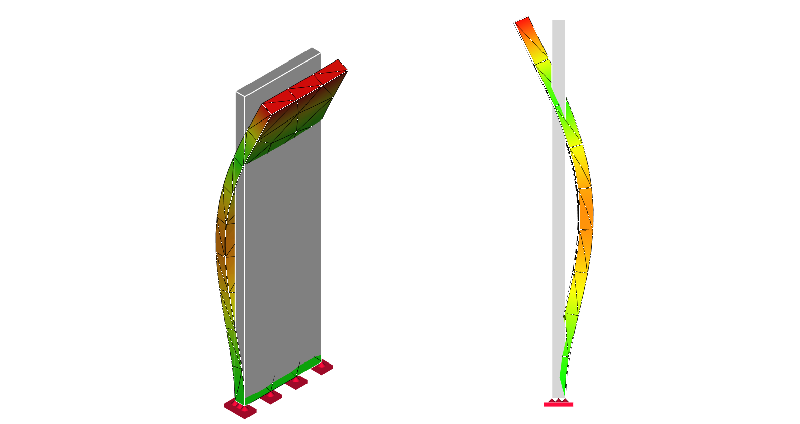
2次モード
3次モード:ねじり
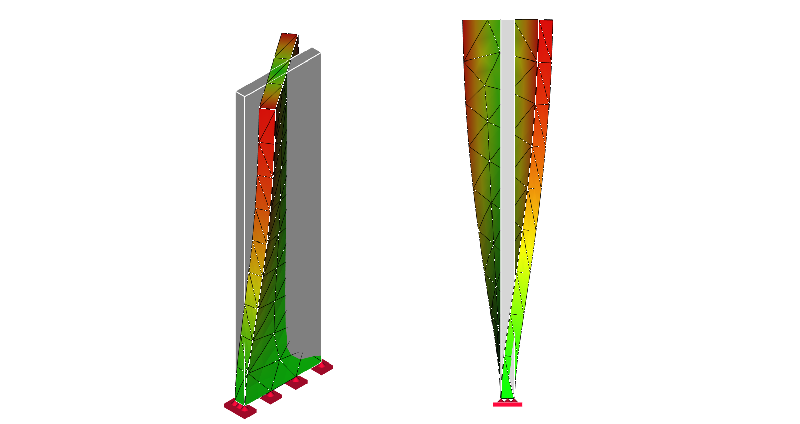
3次モード:ねじり
4次モード:平面曲げ
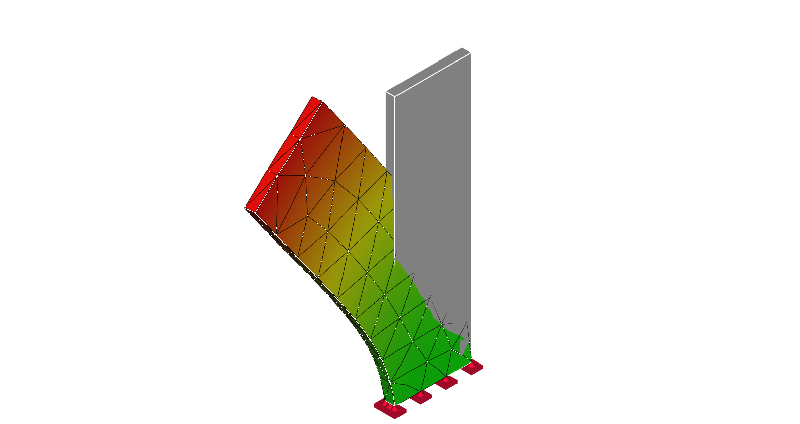
4次モード:平面曲げ
5次モード
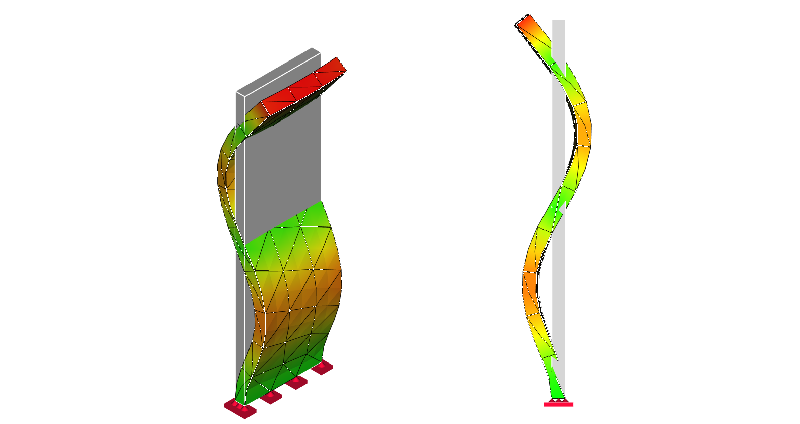
5次モード
6次モード:ねじり
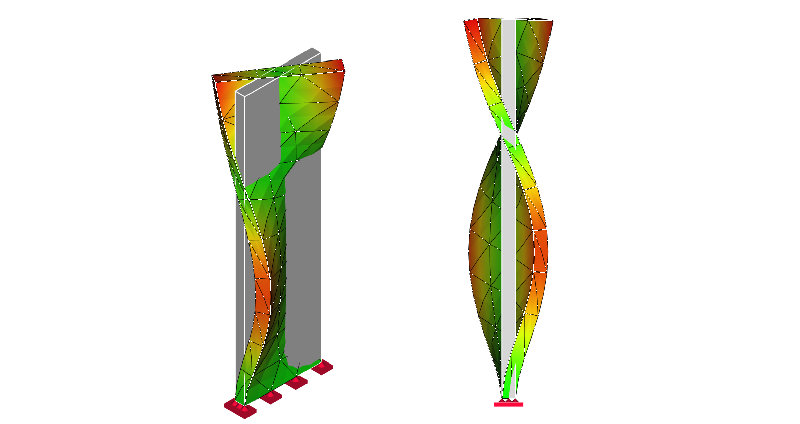
6次モード:ねじり
7次モード
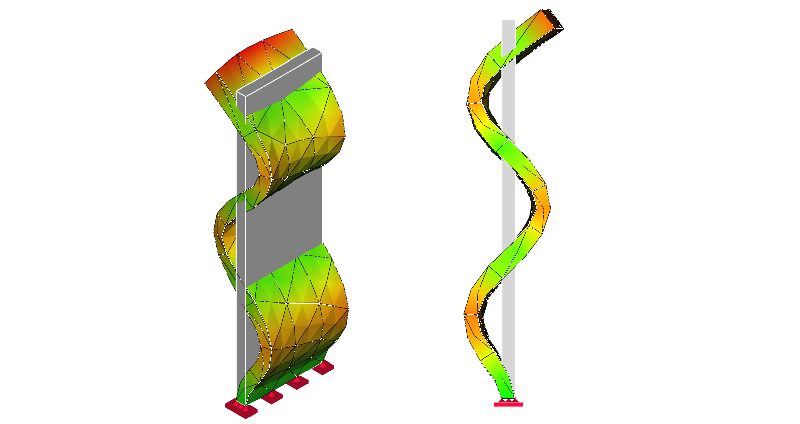
7次モード
8次モード:平面曲げ

8次モード:平面曲げ
9次モード
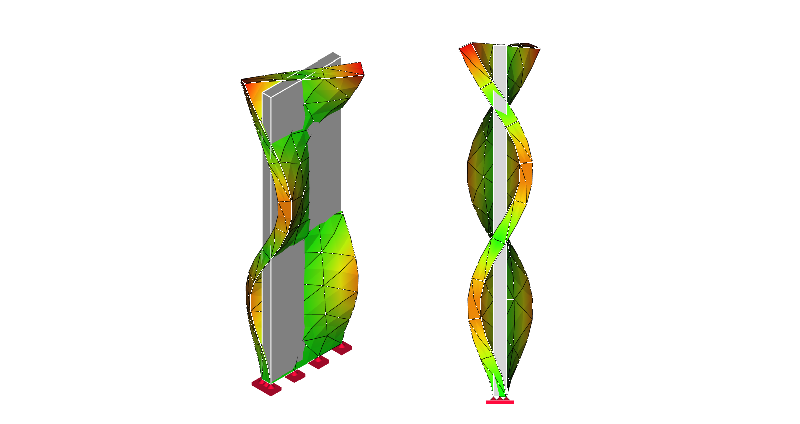
9次モード:ねじり
10次モード:伸び縮み
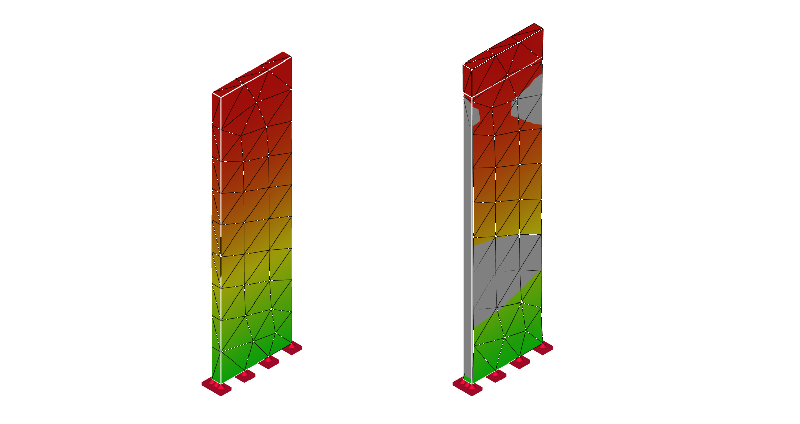
10次モード:伸び縮み
まとめ
ここでは、高層ビルや片持ち梁のような構造物の基本的な振動モード形として、平板の1辺を固定した場合の振動モード形状について説明しました。