自動車の牽引などでレッカー車と乗用車をつなぐ連結金具(シャックル)の設計では、牽引したときに連結金具が壊れないように設計します。
モノづくりの設計では弾性係数や応力を扱いますが、弾性係数には縦と横の2つ、応力には垂直(圧縮、引張)、曲げ、せん断、ねじりの4つがあります。
連結金具のせん断応力を求める問題を例に4つの応力と2つの弾性係数について説明します。
なお、ヤング率(縦弾性係数)や応力の基本については、以下のページをご参照ください。

連結金具に加わるせん断応力
下図に示す連結金具に引張荷重\( F \)を加えた時に、連結金具に加わるせん断応力について考えていきます。

連結金具の設計問題
図1 連結金具の設計問題
連結金具は、以下の3つの部品を組み合わせています。
- 右側のコの字型の部品
- 左側の板状の部品を
- ピン(下図の薄い青色の部品)
ここで、引張荷重とピンを以下の値とします。
引張荷重: \( F = 15,000 \ (N) \ \)
ピンの直径(下図の薄い青の部分):\(\phi 10 \ (mm) \)
この時、ピンの断面積は、
\( ( 10 \div 2 ) \times 2 \times \pi = 314 ( mm^2 ) \)
せん断力は、
\( 15000 \div 2 = 7500 ( N ) \)
※せん断力はピンの2か所にかかるので2で割ります。
この時、
(せん断応力)=(せん断力)/(ピンの断面積)
\( = 7500 \div 314 = 23.9 ( N / mm^2 ) \)
連結金具の材料をSS400とすると、
SS400の引張強さは、
\( 400 ~ 510 ( N / mm^2 ) \)
SS400のせん断応力は、
(SS400の引張強さ)\( \div \sqrt{3} = 231 ~ 295 \)
となります。
ここで安全率を考慮して材料が適切か設計(連結金具とピンの寸法)を決めていくことになります。
以下、応力と弾性係数について説明します。

1つの部品でも、材料の選択、強度設計、安全率を考慮した評価、形状に応じた設計の標準を作っておくと、失敗したノウハウも設計力として積み重ねていくことができると考えています。
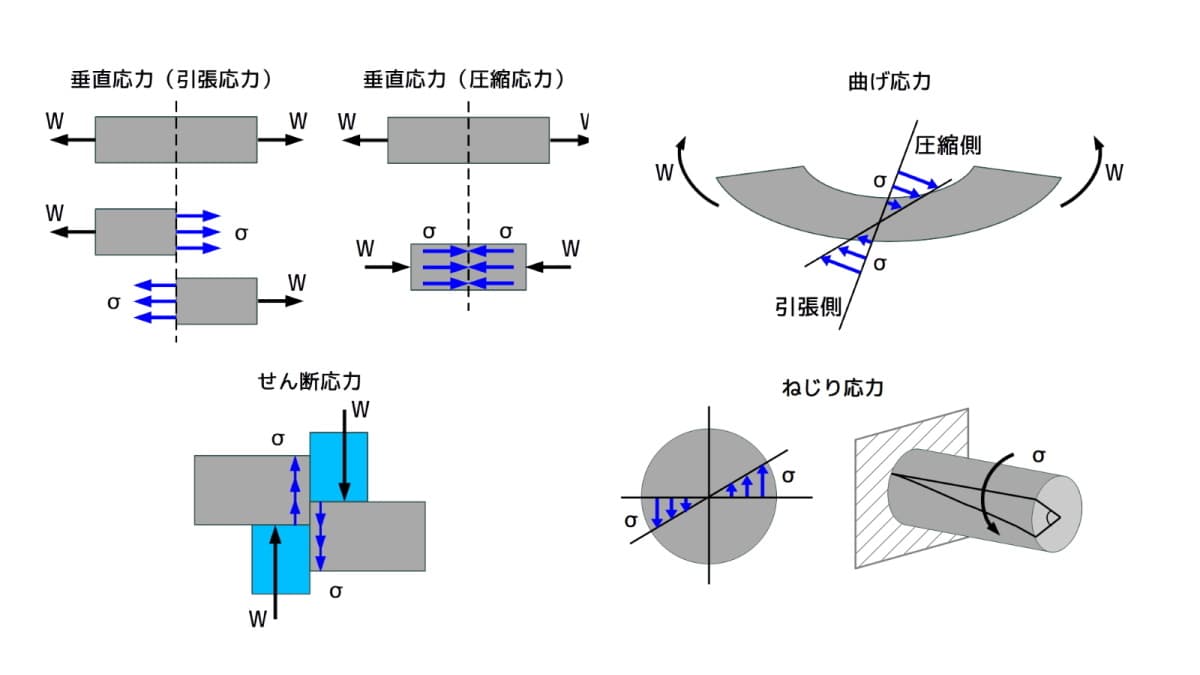
4つの応力:垂直(引張と圧縮)、曲げ、せん断、ねじり
4つの応力について説明します。
ただし、
W:加える力
σ:応力
垂直応力
垂直応力には、引張応力と曲げ応力があります。
引張が進むと破断、圧縮が進むと圧縮破壊となります。

垂直応力(引張と曲げ)
図2 垂直応力(引張と曲げ)
曲げ応力
曲げ応力では、曲げにより圧縮側と引張側が生じます。
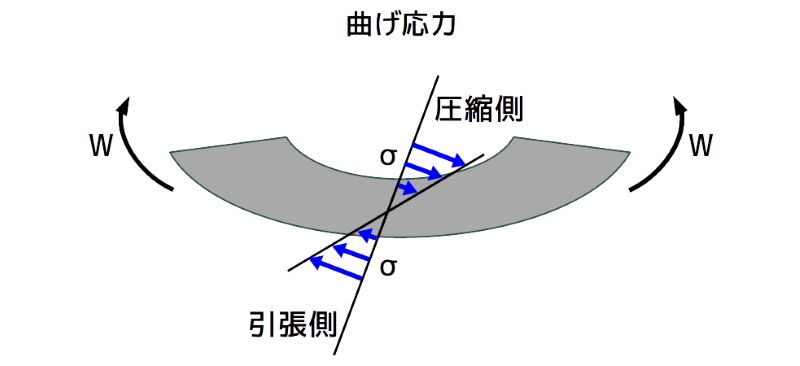
曲げ応力
図3 曲げ応力
せん断応力
部品等のせん断破壊、シャーリングやプレス機械にも関わりの深い応力です。
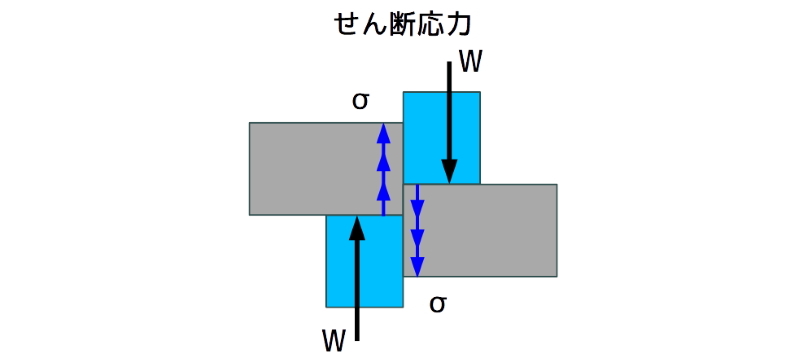
せん断応力
図4 せん断応力
ねじり応力
軸や回転軸などに関わりのある応力です。
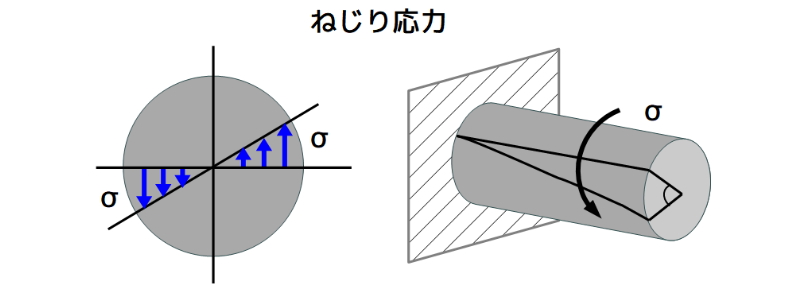
ねじり応力
図5 ねじり応力
縦弾性係数、横弾性係数と応力の関係
縦弾性係数と横弾性係数は弾性係数なので、材料の弾性限度内で使います。
つまり、上述の連結金具のせん断破壊の問題では、弾性がない状態の問題です。
弾性係数と応力との関係は、下表の通りです。
| 縦弾性係数に関係する応力 |
垂直応力(引張、圧縮) 曲げ応力 |
|---|---|
| 横弾性係数に関係する応力 |
せん断応力 ねじり応力 |
下図は、鉄の応力-ひずみ線図です。
A~Eは次の通りです。
A:比例限度
B:弾性限度
C:上降伏点
D:下降伏点
E:引張強さ

比例限度は、荷重を加えても荷重を取り除くと元に戻ります。フックの法則の範囲のことです。

応力-ひずみ線図:鉄
図6 応力-ひずみ線図:鉄

材料の引張試験をやってみると、実際の変形の様子をイメージしやすくなります。
品質保証部などの試験担当部署だけでなく、実際に設計をする技術部署でも教育・訓練に取り入れると、設計や材料選定の力量向上に役立つと思います。
ここで、応力-ひずみ線図に、弾性限度内(薄い青の斜線部分)を図示すると下図の通りです。
せん断破壊についての設計検討であれば、下図の弾性限度内(薄い青の斜線部分)での設計問題ではないことが分かりやすくなると思います。

応力-ひずみ線図と弾性限度内での設計範囲
図7 応力-ひずみ線図と弾性限度内での設計範囲
まとめ
モノづくりの設計では弾性係数や応力を扱いますが、弾性係数には縦と横の2つ、応力には垂直(圧縮、引張)、曲げ、せん断、ねじりの4つがあります。
基本的なことですが、材料の選択、形状設計、応力による評価は標準化していくと設計力が上がっていくと考えています。
ここでは、以下の項目でまとめました。
- 連結金具に加わるせん断応力
- 4つの応力:垂直(引張と圧縮)、曲げ、せん断、ねじり垂直応力
- 曲げ応力
- せん断応力
- ねじり応力
- 縦弾性係数、横弾性係数と応力の関係