ここでは、金属バットのハンマリング試験を行い、バットの周波数応答関数を計測して、計測したデータから振動モード形を作成します。
実験の経験が少なくなっている今、新入社員の体験実習や、シミュレーションと試験(実験、計測)との関係を体験する教材にもなるかと思い、実習を主体とした研修用のテキストとしてまとめています。
Amazonへ:「ハンマリング試験から始めるモード解析入門」
FFTアナライザの使い方については、以下の記事をご参照ください。
はじめに:振動とハンマリング試験
嫌な振動は音から見つかる
機械や家電製品などの騒音や振動問題は、まずは、「うるさい(騒音)」、「変な音がする(異音)」といった音の問題として見つかることが多く、原因調査は騒音や異音がどこから聞こえてくるか、どうして騒音や異音が発生するのかを調べていくことから始まります。
実際には、「この部分(部品)を手で押さえると、音が小さくなる」といった感じで、音が出ている場所や部位(部品)を絞り込んでいきます。
また、音はある部品の振動によって発生していることもあり、この場合、音に関する指摘から始まるトラブルシュートも、最終的には振動対策を施すことになります。
振動の計測とFFTアナライザ
製品等の各部位(部品)から発生する振動は、製品あるいは部品の構造(形状)や材料により決まります。
FFTアナライザによる周波数分析データを利用すれば、対象物のどこから音が出ていて、どの部位が何Hzで振動しているのかを調べることができます。
FFTアナライザによる振動計測のポイントを2つ上げておきます。
- 対象物の振動を精度よく検出できる検出器(センサ)の選定
- FFTアナライザを正しく設定すること
ここでは、金属バットを対象に、FFTアナライザを使い伝達関数を計測し、計測したデータからバットの共振周波数(固有振動数)における簡易的な振動モード形を作成し、どんな風にバットが振動しているのかを可視化します。
ハンマリング試験とは
ハンマリング試験は打撃試験とも呼ばれ、対象物をインパルスハンマで加振し、FFTアナライザで計測します。
インパルスハンマによるハンマリング試験は、準備が簡単で手軽に行えるため、簡単そうに思われがちですが、簡単な方法であるがゆえに、計測者の技術や経験が計測データに大きな影響を及ぼすため意外に奥の深い試験です。


ハンマリング試験の簡単さや難しさについても体験を通して感じてくれると研修もやりがいがあります。
ハンマリング試験に必要な機材とデータ
振動計測に限らず計測をする場合には、「何のために計測をするのか」という目的を明らかにすることが重要です。
計測の目的が不明確なまま初めてしまうと、いたずらに時間ばかり過ぎ、結局やり直すことにもなりかねません。
ここでは、金属バットの振動モード形状を確認したいので、必要な機材やデータは、次の通りです。
- 計測データ:周波数応答関数(伝達関数)
- 計測方法:各計測点の伝達関数をできるだけ同一条件で計測
- FFTアナライザのチャンネル数:最低2チャンネル
- インパルスハンマと加速度センサー
伝達関数(周波数応答関数)の確認に必要なデータ
実験モード解析に必要なデータは、伝達関数(周波数応答関数)があればよいのですが、正しく計測できたかどうかを確認するために、計測時にFFTアナライザで監視(観察)するデータについて説明します。
- 時間軸波形
- パワースペクトラム
- 周波数応答関数(伝達関数)
- コヒーレンス関数
時間軸波形
センサ(インパルスハンマと加速度センサー)の信号レベルとFFTアナライザの電圧レンジが適正かどうか判断することができます。
伝達関数の計測では、インパルスハンマを使い同じ大きさ(FFTアナライザに入力されるレベル)で加振できているかどうか(再現性)を確認します。
また、ハンマリングしている本人には気づかない様なダブルハンマも容易に検出できます。
加速度センサーの信号は、インパルスハンマで加振した対象物の振動の大きさ(FFTアナライザに入力されるレベル)と振動が減衰していく様子を確認します。
パワースペクトラム
インパルスハンマのパワースペクトラムにより、設定した周波数レンジの中で何Hzぐらいまで一様に加振できているかを確認します。
解析に必要な周波数までフラットに加振できていることが望ましく、必要に応じインパルスハンマのチップ変更などを行います。
高い周波数になるほど加振エネルギーが不足するため、ハンマリングによる加振が、回数によらず均一に加振できているかがポイントになります。
応答点(加速度センサー)との関係では、加振点とセンサ取り付け位置が最も遠い位置関係にある場合においても、十分な加振力が得られる(応答点のパワースペクトラムの観測ができる)ことが重要です。
本番の計測に入る前に、応答点を何箇所か選んで、一定の加振力で全ての応答点において必要なパワースペクトラムを観測できるか確認します。
周波数応答関数
周波数応答関数は、(応答点)÷(入力点)のデータです。
周波数応答関数により、ある周波数における応答点の大きさと位相を知ることができます。
- 測定周波数の範囲で何Hz(ヘルツ)が大きい等
- 位相の向き(反転)
また、平均化処理をすることで、データ精度を高めるだけでなく、正しく計測できたかどうかを周波数領域で確認することができます。
コヒーレンス関数
平均化をした場合、1回目と2回目以降のデータの相関をみて、同じようにデータが取れたかどうかを確認することができます。
センサの選定及び設置
バットのハンマリング試験では、加速度センサーをワックス(センサー用の専用ワックス)で固定します。
加速度センサーの選定と設置についてのポイントを以下に示します。
- 計測試料に対して十分に軽く、小さいものを選択する。
- 加速度センサーを取り付けることは、計測対象の固有振動数に大なり小なり影響を与えます。
- センサケーブルの取りまわしなどにも注意する。
- センサケーブルが対象物に接触して、減衰が変化する。
- インパルスハンマで加振したときにセンサーケーブルを引っ張ってしまうと、センサの固定条件が変化し、計測データに影響が出ます。
- 振動モード形を表せる計測点を選ぶ。
- 計測点は、実験モード解析での振動モード形の座標点となるため、観測したい振動モード形をイメージして選定します。
- まずは少ない計測点、計測回数でハンマリングを行い、振動モード形や節の一などの概略イメージをつかみます。
インパルスハンマによる加振方法
インパルスハンマによる計測方法には、加振点移動法と応答点移動法の2つの方法があります。ここでは、加振点移動法を使います。
加速度センサーは、バットのグリップエンドに設置し、加振点はセンサーの反対側とし、順次ハンマリングしていきます。
インパルスハンマの選定・調整(サイズ、チップ)
インパルスハンマによる衝撃力(加振エネルギー)は、幅広い周波数範囲にわたり、ほぼ一定の力からなるため、その周波数範囲にあるすべての共振を起こすと考えられます。
衝撃力の振幅と加振できる周波数範囲は、ハンマのサイズ、長さ、材料および衝撃時の速度によって決まります。一般に加振できる周波数範囲は、衝撃キャップ(チップ)の材料によって決まり、加振エネルギーの大きさはハンマの質量と衝撃時(加振時)の速度によって決まります。
実験モード解析における加振力の調整手順とポイントについて説明します。
- インパルスハンマで試験対象を叩き(ハンマリングし)、FFTアナライザで平均化処理を行います。
- ノイズの影響を減らすため、必ず数回の平均化処理を行います。
- 計測結果を見て、以下の項目について確認します。
- 信号が適切であったか(SN比が十分かどうか)。
- 飽和現象(FFTアナライザへの入力オーバーレンジや、ピークが一定時間平らになる)がないか。
- 計測中に、ときどきインパルスハンマのケーブルやチップなどの接続部をチェックします。接続部が緩むと、センサーの信号が不安定になったり、ノイズが増加することがあります。
- 加振周波数帯域を確認します。
- インパルス波形の周波数波形(パワースペクトラム)が、対象物の共振周波数をカバーしているか。
- 必要に応じチップを変更します。
- チップは衝撃力をセンサーに伝えるとともに、センサー面を保護します。
- 剛性の異なるチップを使用することにより加振力を調整することができます。
- より高い周波数の応答が必要な場合、より硬いチップを使用します。
- 低い周波数の応答をより良くするには、より柔らかいチップを使用します。
- 必要に応じインパルスハンマのサイズを変更します。
- ハンマリングによる加振エネルギーを大きくするには、衝撃の速度かハンマの質量を大きくします。
【参考】主なインパルスハンマのチップと特長
- ハード・チップ(金属製)
- インパルスの立ち上がり方が急峻で、高い周波数まで加振することができます。
- ダブルハンマリング(二度叩き)しやすくなり、パワースペクトル密度は小さくなります。
- ミディアム・チップ(プラスチック製)
- 金属製チップとビニール製チップの間の特性を持ちます。
- ソフト・チップ(ビニール製)
- パワースペクトル密度が大きく、加振エネルギーは低周波数域に集中します。
- 数Hz以下の加振を行うことは困難です。
インパルスハンマの使い方:ここがポイント(コツ)
ハンマリング試験は、計測実施者がインパルスハンマで対象物を加振します。つまり、加振系に人が含まれているため、加振器を使う場合に比べると人の技量や経験が加振の良否に大きく影響を与えます。
以下にハンマリング時のポイント(コツ)を列挙します。


ハンマリングのポイントは、実際にやりながらでないと伝わりにくいため、研修では実際に見せながら説明をするようにしています。習うより慣れるイメージです。
<加振時>
- ハンマはやわらかく軽く支える(握らない)。
- 人の力で叩くのではなく、ハンマの質量を利用して加振することが重要です。
- 叩き方は、できるだけ一様に一定にし、力の調節はハンマ側(大きさ、チップ等)で行います。
- 手はハンマに初速度を与えるだけとする(手で力を加えると加振が乱れ同じような加振ができません)。
<加振点及び方向>
- チップの先端は面積があるので、チップ中心を加振点に一致させるようにする。
- 加振点の位置決めを事前にきちんとしておく(加振点のマーキング)。
- 加振方向は、ハンマの力センサの向きと一致させます。
- ハンマが、対象物表面の法線方向から10度以上傾かないようにします(計測点に対しハンマを垂直に当てるイメージです)。
- 手を含めた加振系で回転運動とならないようにします。
<加振の瞬間>
- 加振の瞬間、ハンマが浮いた状態にあること。手で拘束しない(握らない)。
- インパルスハンマが対象物を叩くのと同時にすばやく引くイメージです。
- 当てるよりも引く方に意識を集中します。
<加振エネルギーを叩き方で調整する場合>
- 人が力の大きさを変えると、熟練者でも再現性を保つのが難しいので極力避けます。
- 単に衝突速度を変えるだけとし、叩く手の力を変えないようにします。
2度叩き(ダブルハンマリング)
2度叩き(ダブルハンマリング)とは、1度目の加振で振動を始めた対象物が、最初の反動で戻ってきたときにハンマと再度衝突してしまう現象のことです。
初心者の場合、ハンマを手で拘束してしまう(握ってしまう)ことが多く、繰り返し同じように叩けない、ダブルハンマとなってしまうことが多いです。
実際に体験させると、何度叩いても2回以上同じように叩けない人もいますので、その際は1回だけのハンマリングデータを使うこともあります。
計測対象物の支持方法
対象物の固定(支持)方法は、計測結果に大きな影響を与えるため、目的に合わせ対象物をきちんと固定(支持)する必要があります。
対象物の固定条件は、自由、固定、弾性支持の3つに分けられますが、バットの伝達関数の計測では、グリップエンド部分を吊るして自由支持としています。
振動モード形と計測点の選定


振動モード形については、まずは計測データから振動モード形を作ってみることを優先しています。
振動モード形とは
ここでは、1本の棒を例に振動モード形について説明します。
物にはその物の構造や材料などにより決定される固有の共振周波数というものがあり、これを固有振動数呼びます。
固有モードは、周波数の低い方から1次、2次、・・・、N次モードと呼ばれ、振動試験で計測する信号には、1次~N次の振動モード、つまり固有振動数が含まれています。
これをイメージにすると下図のようになります。下図は、対象物には、1次モード、2次モード、・・・、N次モードが含まれているというイメージ図です。
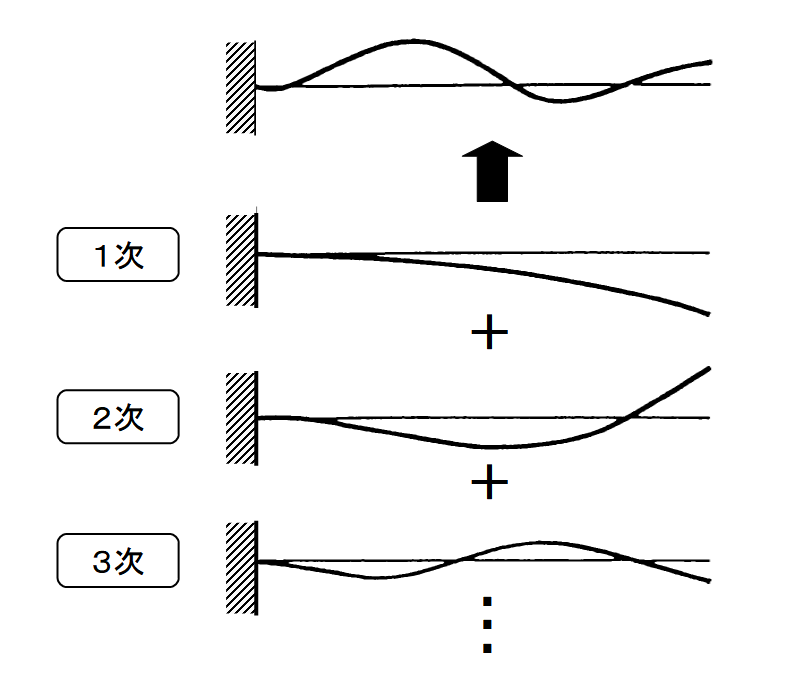

振動モード形のイメージ
計測点数の考え方
基本的には、以下の考え方を組み合わせて、計測点数を決めていきます。
計測点数
計測点は多いほどきれいな振動モード形を得ることができますが、反面計測時間だけでなく計測の難易度(同じように加振する)も高くなるため、全体の振動モード形の傾向(概要)をつかんでから、計測点数を増やしていく方が結果的には効率よく計測及び解析を進めることができます。
確認したい振動モードの個数
多数の振動モード形状を確認したい場合には、伝達関数を計測する周波数範囲を広く(共振周波数の数を多く)設定し、計測点数を減らして対象物がどのような振動をしているのか(固有振動数はいくつ含まれているのか、振動モード形はどのような形か)を把握した後、より詳しく観察したい周波数範囲の計測点を増やし詳細な解析をします。
振動モード形の節と加振点(可制御・可観測)
対象物をハンマリングする際、振動モード形の節を加振した場合には、その振動モード形の共振周波数(固有振動数)は計測できないことに注意が必要です。
同様に、振動モード系の節にセンサを設置した場合には、その振動モード形の共振周波数(固有振動数)は計測(観測)できないことに注意が必要です。
【参考】実験モード解析について
実験モード解析では、対象となる構造物の形状に計測ポイントを定め、その各々のポイントにおける周波数応答関数(伝達関数)の位相とゲイン(大きさ)の情報から、これらの構造物が共振(振動し易い周波数で振動する)した時の振動モード形を可視化します。
実験モード解析には、次のような特長があります。
- 解析対象全体の振動特性を調べる場合に用いる手法
- 共振状態での対象の挙動が可視化されるため、有効な対策を検討しやすくなる。
簡易的な振動モード形の作成
ここでは、ハンマリングにより伝達関数を計測し、得られた伝達関数の大きさと位相から、簡易的に振動モード形状を作成する方法について説明します。
計測の準備
下図に、ハンマリングに必要な計測機材(FFTアナライザ、インパルスハンマ、加速度センサー)の一例を示します。
伝達関数は、グリップエンドに加速度センサーを固定し、インパルスハンマを使った加振点移動法により計測します。
- バットはグリップエンドを糸で吊り、自由支持としています。
- バットのグリップに巻かれているテープは、取り除きます。
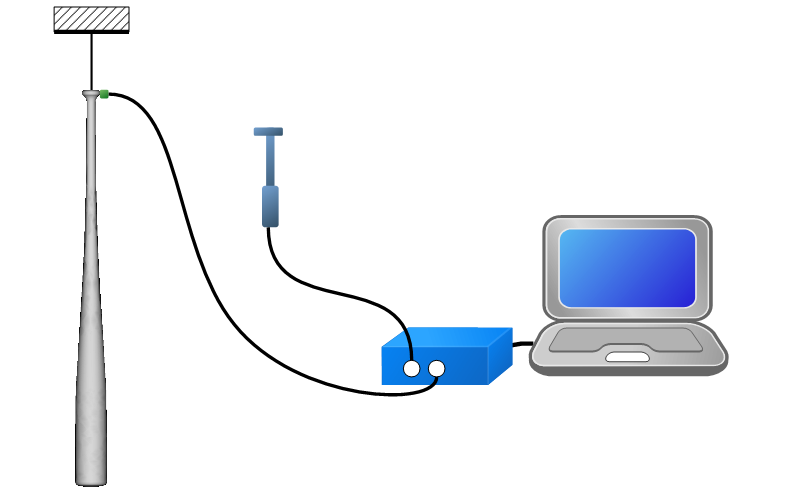

ハンマリングに必要な計測機材の一例
正確なハンマリングのために
正確な振動モード形を得るためには、マーキングした計測点を確実にハンマリングすることが重要です。
- 実験モード解析であれば、目的の振動モード形を表現できる計測点であること
- 計測点を間違えずに計測すること
- 各計測点を正確かつ一様にハンマリングすること
がポイントになってきます。


事前に計測点のマーキング(ハンマリングする場所と計測点番号)をきっちりとしておくことが大切です。
計測手順の概要(FFTアナライザの設定)
計測準備から実際の計測まで、以下について説明します。
①FFTアナライザとセンサの接続
②センサの校正
③周波数レンジの設定
④電圧レンジの調整
⑤トリガの設定
⑥窓関数(ウィンドウ)の設定
⑦平均化の設定
⑧その他の設定(周波数レンジとサンプリング点数)
⑨計測する(ハンマリング)
⑩データの確認
① FFTアナライザとセンサの接続
加速度センサーとインパルスハンマをFFTアナライザに接続します。
インパルスハンマをFFTアナライザのチャンネル1、加速度センサーをチャンネル2に接続します。
② センサの校正
FFTアナライザの単位、校正値を設定します。
インパルスハンマと加速度センサーの電圧値を各センサの基準値に校正することにより、物理量で読み取ることができます。
具体的には、インパルスハンマ、加速度センサーに付属しているデータシートに記載されている感度をFFTアナライザに設定します。
1ch:インパルスハンマ → 加振力の単位N(ニュートン)
2ch:加速度センサー → 加速度の単位(m/s^2)
③ 周波数レンジの設定
実際にハンマリングしながら、目的に合った周波数レンジに調整します。
④ 電圧レンジの調整
電圧レンジは、実際にハンマリングしながらレンジオーバーしない範囲で調整します。
FFTアナライザに入力される信号に応じ、電圧レンジ内でできるだけ大きな振幅となるよう調整します。言葉を変えると、両チャンネルのLEVELインジケータのLEDが赤く(レンジオーバーしない)ならないように、信号波形をなるべく大きくなる様に設定する必要があります。
インパルスハンマによる加振の際は、対象物を叩くのではなく、「インパルスハンマの自重で落とし、ダブルハンマをしないように、加振後素早くハンマを引き上げる」ように、一定の力で対象物を加振します。
これが意外に難しく、実際に体験させてみるとできない人もいます。何度やっても2回同じようにハンマリングができず平均化処理ができない場合には、体験目的であれば1回のみのデータを使うこともありますが、通常は練習する、数をこなすしかありません。
⑤ トリガの設定
波形の観測をしやすくするため、FFTアナライザのトリガ機能を使い、インパルス加振した波形を停止させます。
これまでの設定で、両チャンネルの信号が、レンジオーバーすることなくFFTアナライザに表示されるようになります。
⑥ 窓関数(ウィンドウ)の設定
ハンマリング試験の場合、通常は以下の窓関数が使われます。
1ch:インパルスハンマ:レクタンギュラかフォース
2ch:加速度センサー:レクタンギュラか指数
インパルス加振による信号は、単発的な衝撃信号です。加速度計の応答波形(FFTアナライザの時間軸波形)を見て、1フレーム内で収束しているような場合には、両チャンネルともレクタンギュラ(窓関数なし)の設定にします。
⑦ 平均化の設定
実験(ハンマリング)のばらつきの影響を抑えるため、平均化の設定をします。
【平均化の回数】
バットのハンマリングにおける平均化の回数は、3~5回程度で十分です。
平均化回数で得られる伝達関数の波形を見て、平均化回数が増えても伝達関数の形状の変化(特に共振周波数近傍以外の形状)が小さくなります。
【平均化の方法】
ここでは、パワースペクトル加算平均としています。
【続けてハンマリングする場合の注意点】
続けて加振する場合には、応答が干渉しないように、前回の加振による応答が十分減衰してから次の加振を行います。


バットのハンマリングでは、1回のハンマリングが終わる毎にバットに触れて振動を収束させています。
⑧ その他の設定(周波数レンジとサンプリング点数)
FFTアナライザで解析できる最大周波数(解析周波数レンジ)を設定します。
周波数レンジを決定する要因には、以下のようなものがあります。
- センサ(加速度センサー)の解析周波数範囲内にします。
- 着目する周波数分解能(サンプル点数)
- 同一のサンプリング点数であれば、周波数レンジが低いほど周波数分解能は細かくなります。
- 共振周波数をいくつ(何次)まで見るのか
- 周波数レンジが高いほど、高次モードまで多数の振動モードを見ることができます。
⑨ 計測する(ハンマリング)
以上の設定が完了してから、ハンマリングにより伝達関数を計測します。
計測中は、インパルスハンマと加速度センサーの波形を見ながら、ダブルハンマ(二度叩き)がないかなどを確認しながら行います。
ハンマリングの手順の一例を以下に示します。
- トリガ機能がONになっていることを確認します。
- 平均化ボタンを押すと、FFTアナライザに信号が入力されると自動的に平均化(アベレージ)処理がスタートします。
- ハンマリングを開始します。
- 平均化処理は、設定した回数分のハンマリング(信号入力)が終了すると自動的に停止します。
⑩ データの確認
主なデータの確認方法を列挙します。


実際にハンマリングをしながら説明しています。
コヒーレンス関数を使った確認
- コヒーレンス関数とは、入力と出力信号の相関度を表す関数のことで、FFTアナライザでは、0~1の範囲のレベルで表示されます。
- コヒーレンス関数はその特性上、平均化しないと計算できないため、2回以上の計測が必要となります。
- コヒーレンスが大きい(1に近い)場合、周波数応答関数の信頼性が高いと判断することができます。
計測点を決めるためのポイント
計測点を決めるためには、まずは振動モード形状をざっくりと大雑把につかむことがポイントになります。
例えば特定の振動モード形状を詳細に観察したい場合には、あらかじめ振動モード形状の全体を確認してから、詳細に観察したい部分の計測点を増やすことにより、全体のモード形状と観察したい部分の振動状態を分析しやすくなります。
計測データによる確認方法
伝達関数の計測で、データが正しく取れているかどうか確認する方法を列挙します。
- インパルスハンマの時間軸波形
- 計測開始時に残留振動がないか、ダブルハンマになっていないか。
- 加速度センサーの時間軸波形
- 例えば、残留振動がないか、自然に減衰しているか。
- インパルスハンマのパワースペクトラム
- 計測したい周波数まで加振できているか。
- コヒーレンス
- 平均化の具合
- 例えば3回目の加振をしたら急にスペクトラムの形状が乱れた。
経験による方法
ハンマリングの経験を重ねると、ハンマリング時の打音の変化や加振時の感触などでも、うまく加振できているかどうか判断できるようになります(とは言っても個人差が大きいです)。
いずれにしろ、計測の練度向上(うまくインパルスハンマで加振できる)に伴い、効率よく計測を進めることができるようになります。
ハンマリング試験による周波数応答関数(伝達関数)の計測
計測対象のバットは減衰が小さいため、ハンマリングによる応答が収束する前に、次のハンマリングをしてしまう可能性があります。
このため、計測が終了した後、バットに手を触れ、残留振動とバットの揺れを抑えてから次のハンマリングを行います。
計測点を下図に示します。計測点は5か所、センサは計測点1の反対側に設置します。
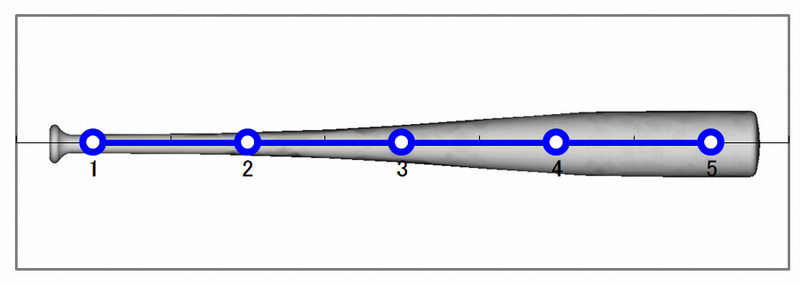

バットの計測点
下図は、周波数応答のゲイン(アクセレランス)、位相の計測データの一例です。
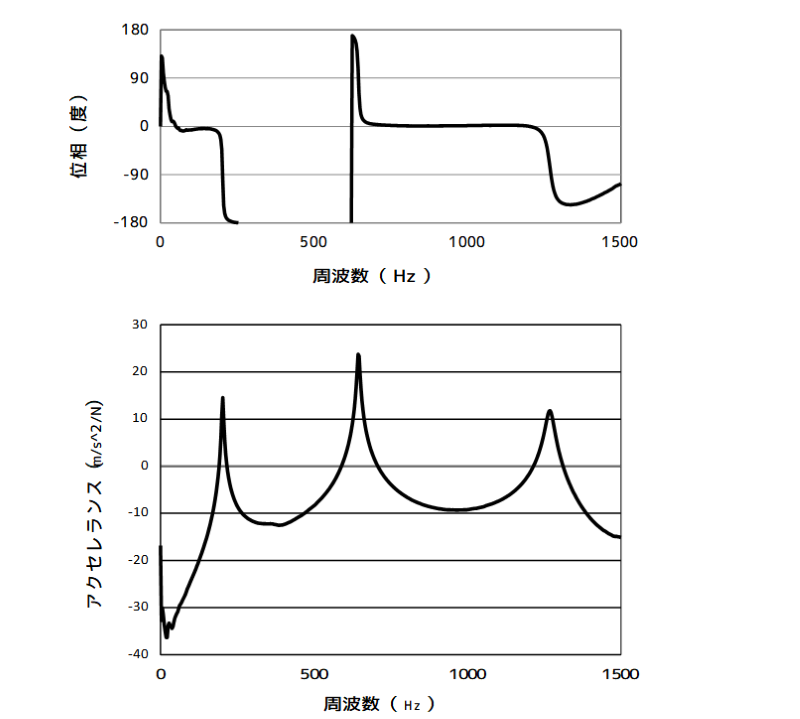

周波数応答関数のデータ例
データ処理:簡易的な振動モード形状の作成
ゲイン(振動の大きさ)及び位相(振動の向き)データ整理
計測した周波数応答関数から、以下の表を作成します。
バットの1次から3次モードの共振周波数における周波数応答関数の大きさ(ゲイン)の値と位相(プラスかマイナスか)を記入します。
| 計測点 | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 1次モード | 43 | 33 | 39 | 25 | 35 |
| 位相 | + | - | - | - | + |
| 2次モード | 35 | 44 | 34 | 34 | 34 |
| 位相 | + | - | + | + | - |
| 3次モード | 11 | 9 | 15 | 15 | 13 |
| 位相 | - | - | + | - | + |
表 計測結果の一例
振動モード形の作成
表計算ソフトを使ったバットの振動モード形の作図例を以下に示します。
上からバットの1次、2次、3次モードです。
計測点を増やすとより滑らかな振動モード形を得ることができます。
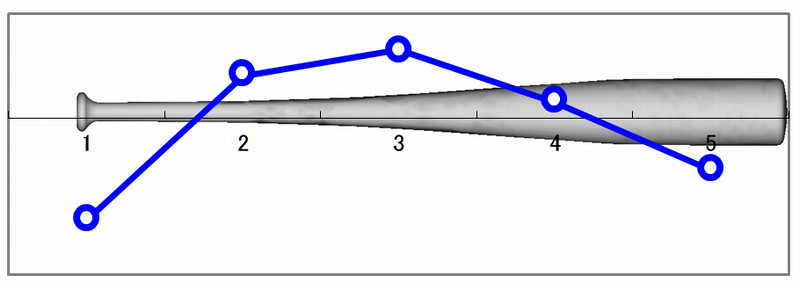

バットの1次モード
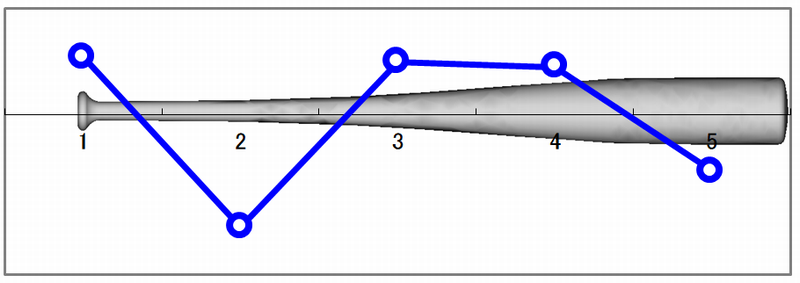

バットの2次モード
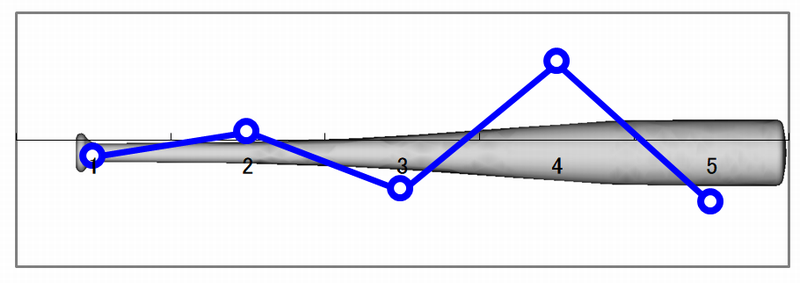

バットの3次モード
表計算ソフトを使った振動モード形の作図例
考察:ホームランを振動から考える


時間的余裕があれば、これまでの内容から仮説と検証の1例として考察を加えるとよいと思います。
ここでは、ホームラン(打球を遠くに飛ばす方法)について、振動モード形を使って考察します。
バッティングについて考える(実現象を簡略化)
バッティング、ピッチャーが投げたボールを打つこととは、どのような現象、動きなのか、ホームランはどのような場合に打てるのかについて考えてみます。
実際のバッティングは、ピッチャーが投げたボールをバッターが打つことなのですが、このままではホームランについて考察するための条件が多すぎます。
例えば、
- ピッチャーが投げるのは直球(ストレート)のみとしても、コース、スピード等様々です。
- バッターのスイングは、アッパースイング、ダウンスイング、水平等、ボールに当たる角度(スイングの角度)が様々です。
そこで、ホームランとなる場合のバッティングをできるだけ簡略化します。ここでは、次のように考えています。
- ホームランは、静止したボールをバットで叩き、最も遠くに飛ばすこととする。
- 遠くに飛ばすには、バットがボールに接触(インパクト)する瞬間に、スイングにより発生した運動エネルギーを、バットを介して振動(エネルギーをロス)することなくボールに伝えればよいとする。
- バットを握ることによる影響(減衰が大きくなる等)は、無視する。
下図は、バッティングを簡略化したイメージです。
- ボールは静止している。
- スイングは同一平面内とする。
- ホームランは、スイングによるエネルギーが最も多くボールに伝わることとする。
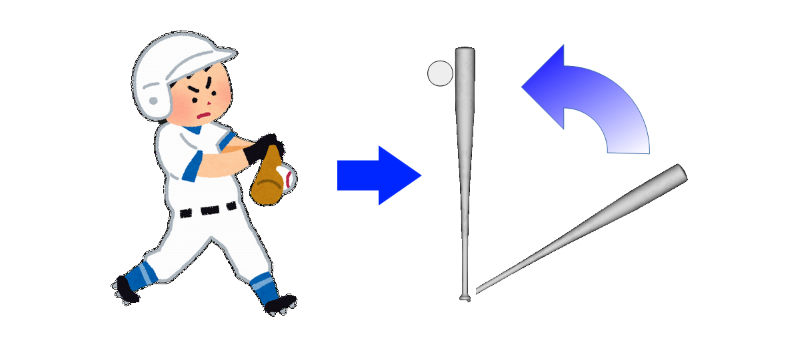

バッティングの簡略化イメージ
バッティングの経験について考える
野球やソフトボールで、ホームランを打った(いい当たりだった)ときには、「バットにボールが当たった感じがしない」といったことを聞いたり、自ら体験したことがあるのではないでしょうか。
下図の1次の振動モード形について考えてみます。


バットの1次モード
振動モードの節で打つとホームラン?
バットの1次モードには、上図の4から5の間に振動モードの節があります。バットの1次の振動モードの節に力を加えた場合、1次モードは励起されない、つまり、バットに振動が発生しません。
したがって、バットの1次モードの節でボールをとらえることができれば、バットのスイングによる運動エネルギーが最大限ボールに伝わると考えることができます。
つまり、ホームランはバットの節で打っていると考えられ、「ホームランを打った時には打った感触がない。」という経験も説明できます。
振動モードの腹で打つとつまって手がしびれる?
1から2の間のグリップ上部は、1次の振動モードの腹があります。振動モードの腹をに力を加えると、そのモードが励起されます。つまり、バットが振動します。
「バットの根元にボールが当たると手がしびれる」という現象は、振動モード形から考えると、バットの腹で打った場合に発生すると考えられます。
2次及び3次モードについても、グリップ上部の1次モードと同じような位置に各振動モードの節があることから、野球でつまった場合に手がしびれる経験とも一致していると考えられます。
考察の一例
ここでは、バッティングという現象を簡略化し、バットの周波数応答関数から簡易的な振動モード形を作成し、考察することにより、次のことが分かりました。
- ホームランは、バットの節で打っていると考えることができる。打った感触がないという経験とも一致する。
- つまった場合は、バットの節で打っていると考えることができる。手がしびれる経験とも一致する。
以上、ホームランについて仮説を立て、実験で得た周波数応答関数から簡易的な振動モード形を作成し、仮説を検証しました。
まとめ
ここでは、実験の経験が少なくなっている今、新入社員の体験実習や、シミュレーションと試験(実験、計測)との関係を体験する実習をイメージして、振動計測の1つハンマリング試験について、金属バットを対象に選びFFTによる周波数応答を計測、データから振動モード形を作成し考察した例を以下の項目で説明しました。
- はじめに:振動とハンマリング試験
- ハンマリング試験とは
- センサの選定及び設置
- インパルスハンマによる加振方法
- 計測対象物の支持方法
- 振動モード形と計測点の選定
- 簡易的な振動モード形の作成
- ハンマリング試験による周波数応答関数(伝達関数)の計測
- データ処理:簡易的な振動モード形状の作成
- 考察:ホームランを振動から考える



