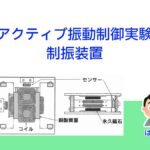
ここでは、センサーとアクチュエータの配置についての実験と考察について説明します。
スカイツリーや超高層ビルの様な柔軟構造物の振動制御においては、次の2つの課題があります。
(1)低次元化モデルの作成とスピルオーバー対策
(2)センサーとアクチュエータの配置
(2)は、コロケーションに関する課題です。
一般に、センサーとアクチュエータの位置が一致する場合をコロケーションと呼びます。
コロケーションが成立しない場合には、単純な出力フィードバックでゲインを大きくしていく(制御を強くかけていくと)と不安定になってしまいます。
また、柔軟構造物の振動モードの節においては、不可制御、不可観測となるように、センサーとアクチュエータの位置により可制御性と可観測性が変化し、ひいては制振性能そのものも変わってきます。
以下、柔軟構造物の振動制御におけるセンサーとアクチュエータの配置についての実験と考察について説明します。
センサーとアクチュエータの配置に関する考察
一般に、センサーとアクチュエータ設置点が異なる場合には、コロケーションが成立しないため(制御的には非最小位相系となるため)、単純な出力フィードバックによりゲインを増大させる(制御を強くして制振効果を高めようとすると)と不安定になります。
これは、柔軟構造物の振動モードの節においては、不可制御、不可観測となるように、センサーとアクチュエータの設置位置が、制振性能そのものに影響を及ぼすということです。
このため、「振動モード形を利用したモデリング入門」では、振動モード形の節が持つ不可制御・不可観測性を活用し、この点を質点として低次元化モデルを作成しています。
一方、実際の構造物の振動制御を行う場合には、構造的制約から制振装置設置位置に制約がある場合も考えられます。

センサーについては、ほぼ任意の位置への設置ができると考えられます。むしろ、センサーの長期安定動作やメンテナンス面での制約の方が大きいのではないでしょうか。
この場合、センサーとアクチュエータの設置位置を振動モード形の節からずらした場合の制振効果が問題となります。
そこで、センサーとアクチュエータの配置と制振効果との関係の初めの一歩として、1自由度系モデルによる塔状構造物の振動制御を例に、センサーとアクチュエータの配置が制振効果に与える影響について考察した例を次の順で説明します。
- 制振装置を制振対象の任意の位置に設置し、この点で制振対象の低次元化モデルを作成します。
- センサーを2次モードの節から移動させ、同一の低次元化モデルにより制御を行い、センサーの設置位置が制御系の安定性にどのような影響を与えるかについて実験的に考察します。
振動モード形とセンサー設置位置の分類
下図に、実験に使用した塔状構造物の概要を示します。
塔状構造物は、高さ1500mm、断面が30mm×60mm、厚さ2.3mmの鋼製角パイプ(中空の鋼製角柱材)です。
角パイプ下端を垂直にベースプレートに溶接し、これを定盤に固定しています。
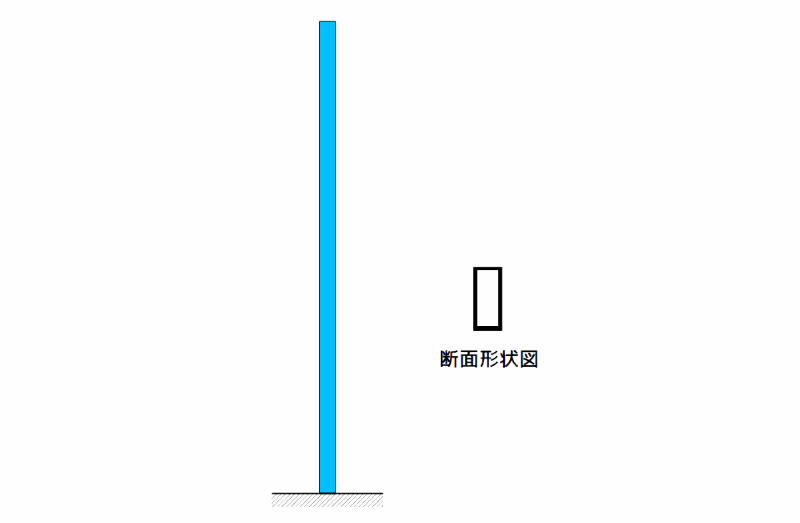
塔状構造物の概要
図1 塔状構造物の概要
下図に、実験モード解析により得られた塔状構造物の振動モード形と制振装置設置位置で作成した1自由度系低次元化物理モデルを示します。
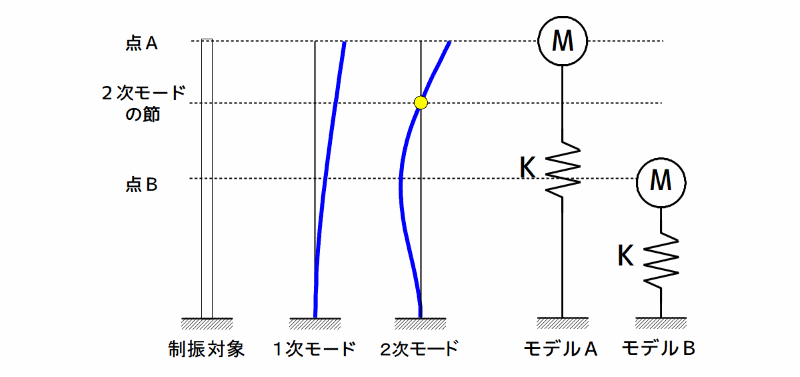
塔状構造物の振動モード形と物理モデル
図2 塔状構造物の振動モード形と物理モデル
モデルAは、ハイブリッド動吸振器を制振対象先端の点Aに設置した場合、モデルBは、制振対象中間付近の点Bに設置した場合を示します。
ここで、2次の振動モード形に着目すると、制振装置設置位置は、2次モードの節(図2の黄色の丸印部分)とその上下に分類することができます。
2次の振動モードの節に制振装置を設置し、この点で1自由度系低次元化モデルを作成した場合、2次モードは、不可観測であると同時に不可制御であるため、2次モードによるスピルオーバーは発生しません。
そこで、ハイブリッド動吸振器設置位置を2次の節の上下に分け、それぞれの代表点として、2次モードの振幅の大きい、構造物の最上部(点A)と 中央部(点B)を選び、この点で塔状構造物の1自由度系低次元化モデルを作成します。
制御系はLQ最適制御理論で設計し、センサーを移動させた場合の制振効果について実験により考察します。
また、制振対象をモデル化した点は、2次の振動モードの最大振幅に近い場所であり、作成した1自由度モデルを用いてLQ制御理論により振動制御を行うと、無視した2次以上のモードによるスピルオーバーの発生が懸念されます。
このため、「振動モード形を利用したモデリング入門」においては、センサーの設置位置を2次モードの節に変更し、2次モードの不可観測性によりスピルオーバーを防止しています。
そこで、まず、センサーを2次モードの節に設置し、「振動モード形を利用したモデリング入門」のモデリング法の有効性を実験により確認します。
次に、センサーの位置を2次モードの節から移動させた場合の同一制御モデルによる振動制御実験を行い、センサーの位置が制御系に与える影響について考察します。
振動制御実験

この実験、制御かけると不安定となる(発振する)実験なので、発振し始めたなら直ちに制御を切らなけいと制振装置が壊れてしまいます。結構、ドキドキしながら実験してたことを思い出します。
実験装置及び実験方法
前節で作成した力学モデルは、制振装置設置位置で作成したものであるため、2次モードの節で検出した絶対変位を用いて制御する場合、検出された変位信号に何らかの修正を加える必要があります。この場合には、1次の振動モード形から修正することができます。
制御系は、LQ制御理論を使って設計しています。
実験装置の構成を下図に示します。
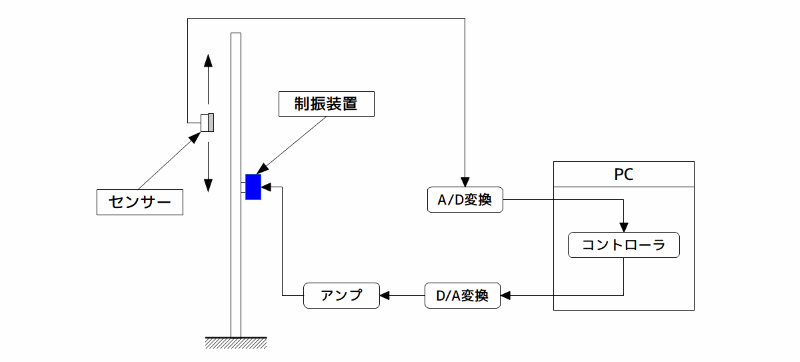
実験装置の構成
図3 実験装置の構成
コントローラーには、PC(パソコン)を使用しています。
制振対象の絶対変位と相対変位は、A/D変換器を介してPCに入力され、この変位信号から差分により速度信号を得ています。
これら4個の状態量に、重み係数に応じて算出したゲインを乗じて制御量を決定します。
D/A変換器から出力した制御信号をアンプで増幅した後ハイブリッド動吸振器を駆動し、塔状構造物の振動制御を行なっています。
実験は、ハイブリッド動吸振器設置点をインパルス加振し、この時の時間応答を評価しています。
なお、使用したハイブリッド動吸振器は、下図に示す動吸振器型のハイブリッド動吸振器です。
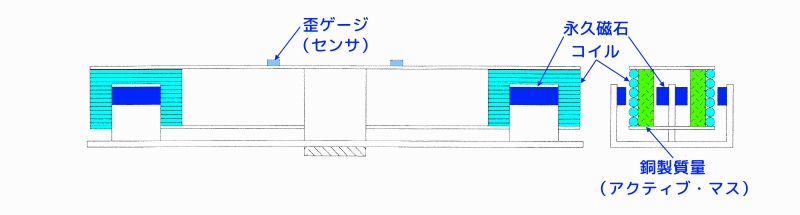
動吸振器型ハイブリッド動吸振器
図4 動吸振器型ハイブリッド動吸振器
上図のハイブリッド動吸振器は、二重動吸振器の質量部にコイルを巻いてハイブリッド・マスとしています。
- 図中に示す2組の永久磁石とコイルにより発生する電磁力により、ハイブリッド・マスを駆動させています。
- ハイブリッド・マスを導体である銅で作ることにより、これが磁場内で磁束と直交して運動(移動)する際に渦電流が発生し、運動と逆向きの磁気減衰力を得ることができる構造となっています。
この様に、ハイブリッド・マスには磁気減衰力と電磁力が同時に作用する構造となっており、パッシブ動吸振器とアクティブ動吸振器の特性を兼ね備えたハイブリッド動吸振器を実現しています。
実験結果
実験結果について、以下に分けて説明します。
- センサーを2次モードの節に設置した場合
- ハイブリッド動吸振器設置位置による比較
- 制振装置とセンサーの配置による比較
センサーを2次モードの節に設置した場合
センサーを2次モードの節に設置し、パッシブ動吸振器としての制振効果を確認します。
下図に、センサーを2次の節に設置し、ハイブリッド動吸振器を点A(最上部)と点B(2次モードの腹)に設置した場合のハイブリッド動吸振器の有無によるインパルス応答(時間応答)の比較を示します。
細線がハイブリッド動吸振器の無い場合、太線がハイブリッド動吸振器を設置した場合の時間応答です。
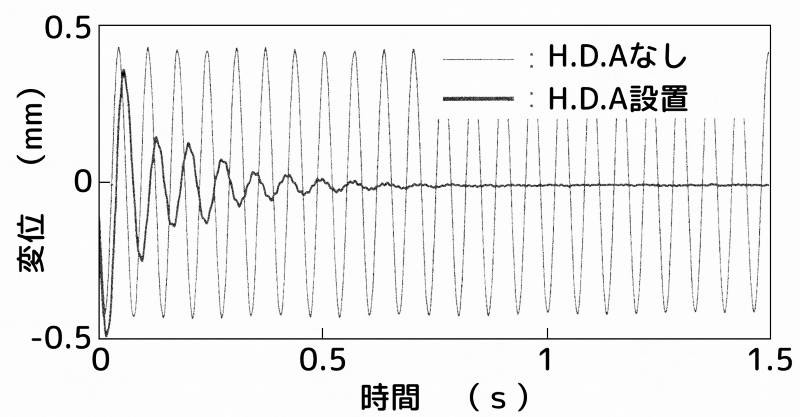
ハイブリッド動吸振器を点A(最上部)に設置
図5 ハイブリッド動吸振器を点A(最上部)に設置
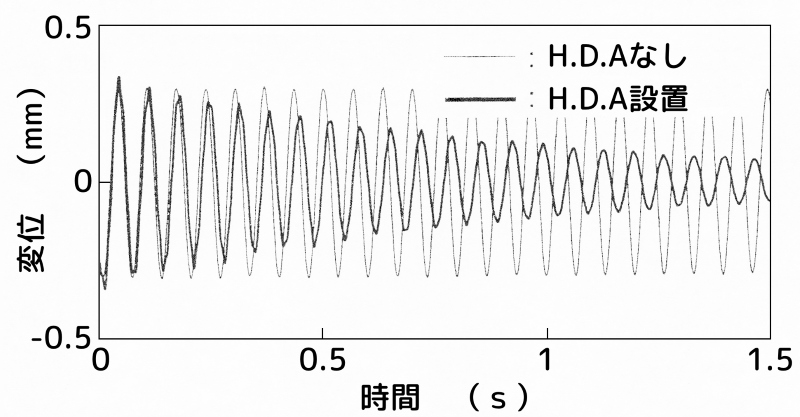
ハイブリッド動吸振器を点B(2次モードの節)に設置
図6 ハイブリッド動吸振器を点B(2次モードの節)に設置
両図より、
- ハイブリッド動吸振器なしでは、外乱による振動がほとんど収束しない。
- ハイブリッド動吸振器を設置すると、そのパッシブ動吸振器の効果により良好な制振効果を得られる。
- パッシブ動吸振器としての制振効果は、2次モードの振幅が大きい塔状構造物先端部(点A)の場合の方が高い。
ことが分かります。

なお、パッシブの制振効果は、ハイブリッド動吸振器のパッシブ系の最適設計により高めることが可能です。
この様に、ハイブリッド動吸振器は、何等かの原因でアクティブ制御の機能が発揮されない場合においても不安定とならない、信頼性の高い制振装置であることを確認できます。
ハイブリッド動吸振器設置位置による比較
図7、図8に、ハイブリッド動吸振器(制振装置)をそれぞれ、点A、点Bに設置し、制御を掛けた場合のインパルス加振実験での時間応答を示します。
図(a)、図(b)、図(c)は、それぞれセンサーを点A、2次モードの節、点Bに設置した場合です。
制振対象の質点のみに重みを掛け、同じ重み係数で制御しています。
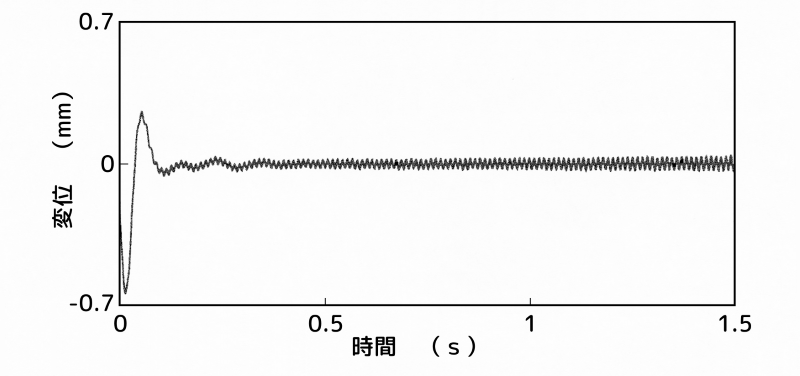
制振装置:A点(最上部)、センサー:A点(最上部)
(a)センサー:A点(最上部)
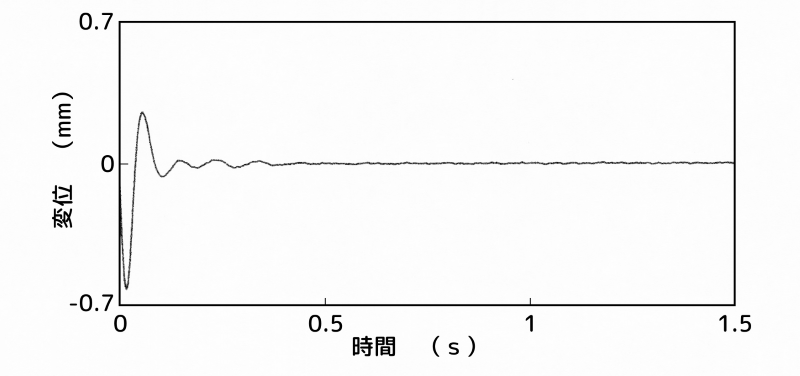
制振装置:A点(最上部)、センサー:2次モードの節
(b)センサー:2次モードの節
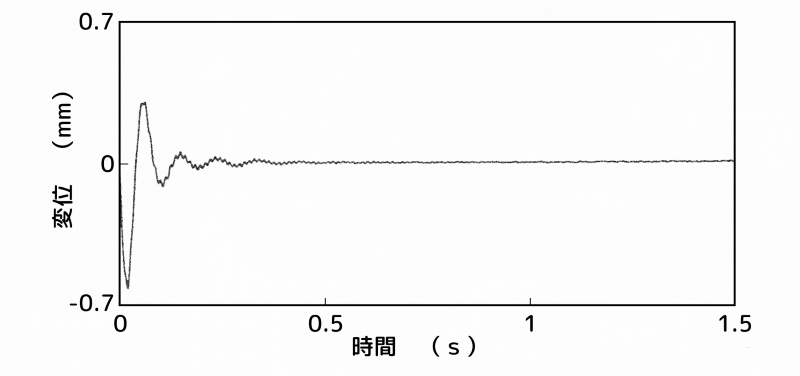
制振装置:A点(最上部)、センサー:B点(2次モードの腹)
(c)センサー:B点(2次モードの腹)
図7 A点(最上部)にハイブリッド動吸振器を設置した場合のインパルス応答
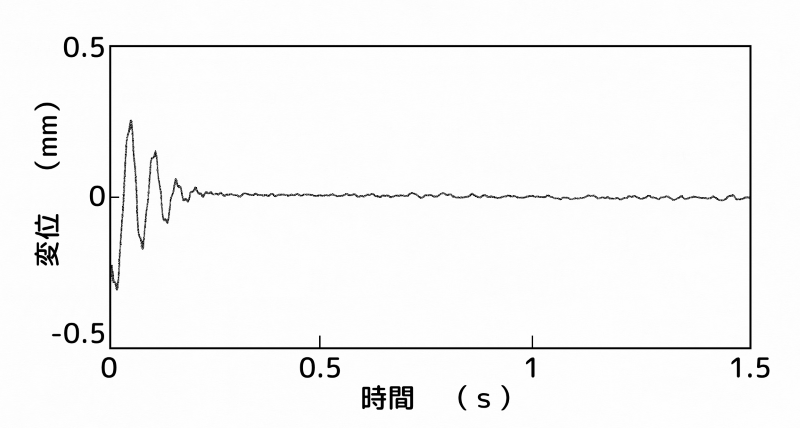
制振装置:B点(腹)、センサー:A点(最上部)
(a)センサー:A点(最上部)
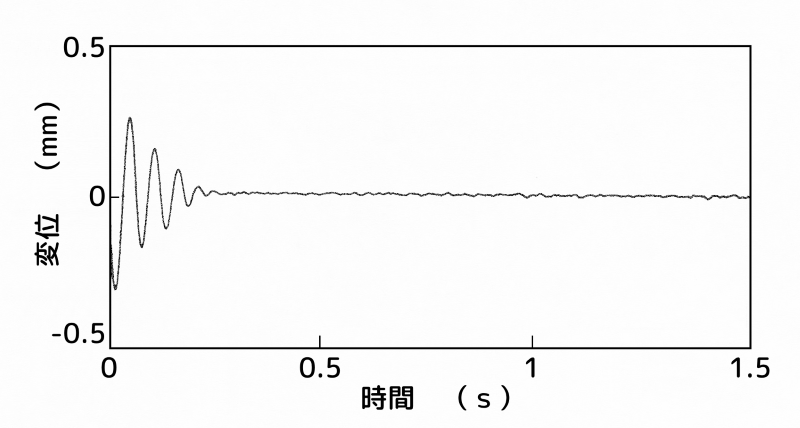
制振装置:B点(腹)、センサー:2次モードの節
(b)センサー:2次モードの節
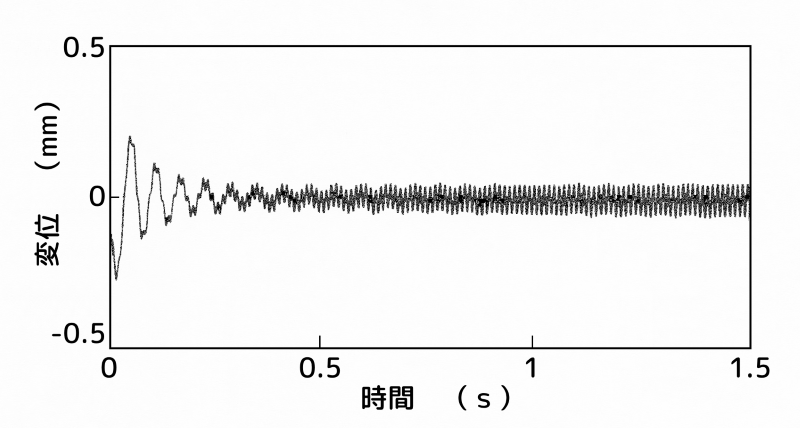
制振装置:B点(腹)、センサー:B点(2次モードの腹)
(c)センサー:B点(2次モードの腹)
図8 B点(2次モードの腹)にハイブリッド動吸振器を設置した場合のインパルス応答
両図(b)から、センサーを2次モードの節に設置した場合には、不可観測性により、ハイブリッド動吸振器の設置位置にかかわらず、良好な制振効果が得られていることが分かります。
一方、センサーを2次モードの節以外に設置した場合には、モデリングの際に無視した2次モードの振動も検出することになります。
このため、2次モードの節を境にして、制御系の特性が不安定となりスピルオーバーが発生する側と、2次の節の場合に比べて制御性は劣るものの不安定とはならない側とが存在します。
図7-(a)と図8-(c)は、不安定側であり、スピルオーバー現象を確認できます。
一方で、図7-(c)と図8-(a)は、2次モードを検出しているにもかかわらず、不安定とはなっていないことが分かります。
以上の実験結果を整理すると、次のことが明らかとなります。
- センサーを2次モードの節に設置した場合、ハイブリッド動吸振器の設置位置によらず、最も良好な制振効果を得ることができる。
- センサーを2次モードの節以外に設置する場合、ハイブリッド動吸振器設置点とセンサー設置点とが、2次の振動モード形の節を挟む位置関係にある時、2次モードの節に設置した場合に比べると制振性能は劣りますが、制御系は安定でありスピルオーバーは発生しない。
制振装置とセンサーの配置による比較
ハイブリッド動吸振器とセンサー設置点が、制御系の安定性に与える影響を伝達関数の実測結果から考察します。
ここでは、入力点をハイブリッド動吸振器設置点、応答点をセンサー設置点としています。
図9に、ハイブリッド動吸振器をA点(最上部)に設置し、センサーをA点(最上部)、及び、点B(2次モードの腹)に設置した場合の制振対象の伝達関数を示します。
同図(a)がA点(最上部)、同図(b)が点B(2次モードの腹)の応答です。
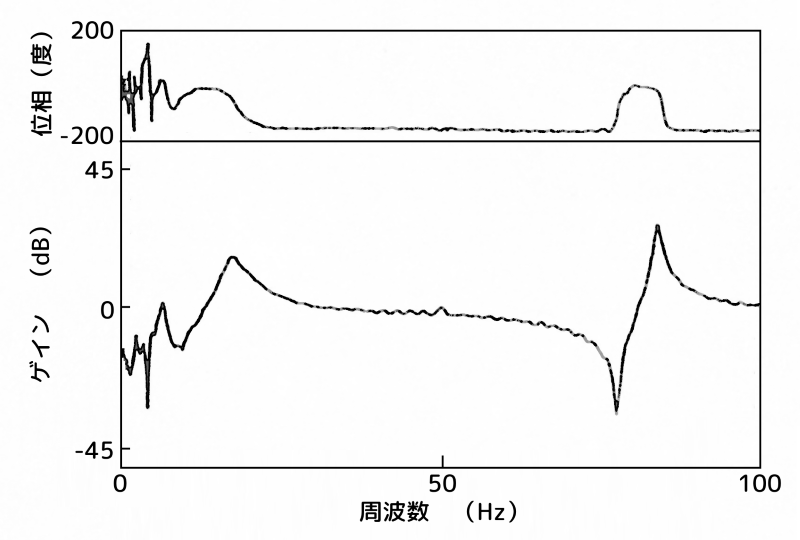
制振装置:A点(最上部)、センサー:A点(最上部)
(a)センサー:A点(最上部)
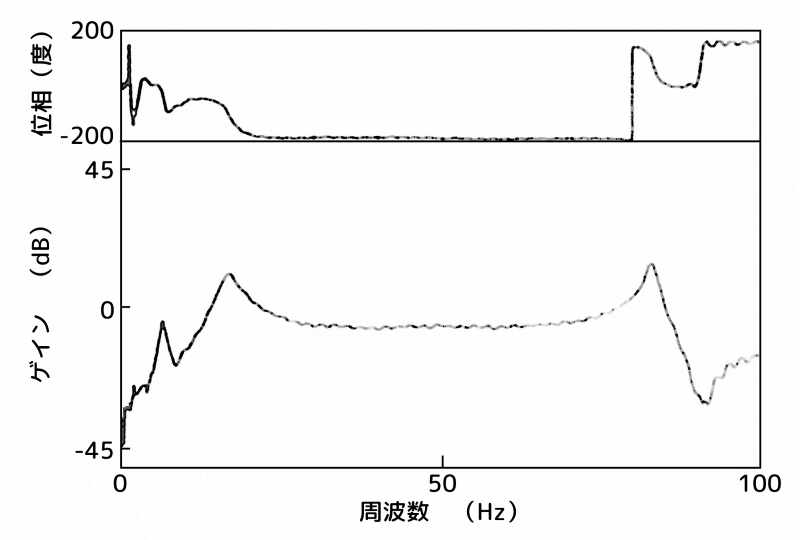
制振装置:A点(最上部)、B点(腹)
(b)センサー:B点(2次モードの腹)
図9 ハイブリッド動吸振器をA点(最上部)に設置した場合
ここで、位相に注目すると、コロケーションが成立していることを示す 位相が0°~180°の範囲内にあるA点(最上部)の場合は安定だと考えられます。
しかし、実際には、制御量を大きくする(制御を強くする)に従いモデリングの際に無視した2次モードの共振ピークが成長し、ついにはスピルオーバー現象を生じます。
一方、2次モードの共振ピークを越えると360°の位相差を生じる点B(2次モードの腹)の応答は、制御量を増大させた場合においても2次モードによるスピルオーバー現象を生じることなく、1次モードを良好に制御しています。
図10に、ハイブリッド動吸振器を点B(2次モードの腹)に設置し、センサーをA点(最上部)、及び、点B(2次モードの腹)に設置した場合の制振対象の伝達関数を示します。
同図(a)がA点(最上部)、同図(b)が点B(2次モードの腹)の応答です。
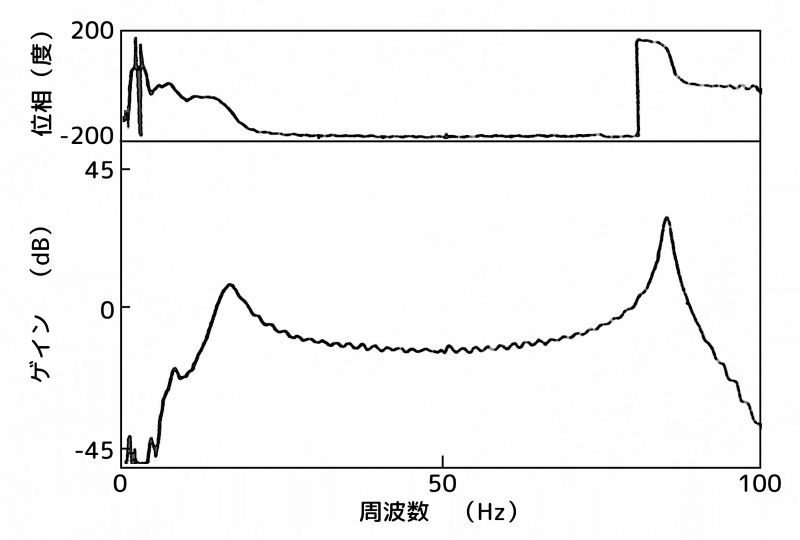
制振装置:B点(腹)、センサー:A点(最上部)
(a)センサー:A点(最上部)
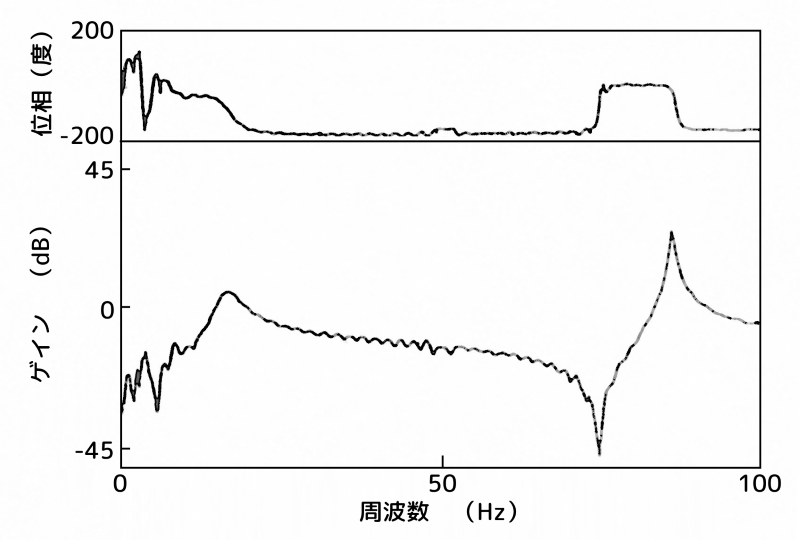
制振装置:B点(腹)、センサー:B点(腹)
(b)センサー:B点(2次モードの腹)
図10 ハイブリッド動吸振器をB点(2次モードの腹)に設置した場合
同様に位相に注目すると、コロケーションが成立している範囲内にある 点B(2次モードの腹)の場合は、安定であると考えられます。
しかし、実際には、制御量を大きくするに伴いモデリングの際に無視した2次モードの共振ピークが成長し、ついにはスピルオーバー現象を生じます。
一方、2次モードの共振ピークを越えると360°の位相差を生じるA点(最上部)の応答は、制御量を増大させた場合においても2次モードによるスピルオーバー現象を生じることなく、1次モードを良好に制御しています。
以上の結果を整理すると、1次モードと2次モードの共振周波数の間に反共振が現れる場合、つまり、2次の節を挟むようにハイブリッド動吸振器とセンサーを設置した場合、その制御系は安定となっています。
コロケーションが成立しない場合において、この様な実験結果を得られたことは興味深いと考えています。

今でも不勉強で理由を理解できていません。
実験結果と考察
これまで述べてきた実験結果を整理して模式的に表したのが下図です。
同図において、
- 計測点1がA点、計測点8がB点
- 水色のH.D.Aの部分は、ハイブリッド動吸振器(制振装置)設置位置
- 黄色の三角形の部分は、2次モードによるスピルオーバー現象の強さ(イメージ図)
を表しています。
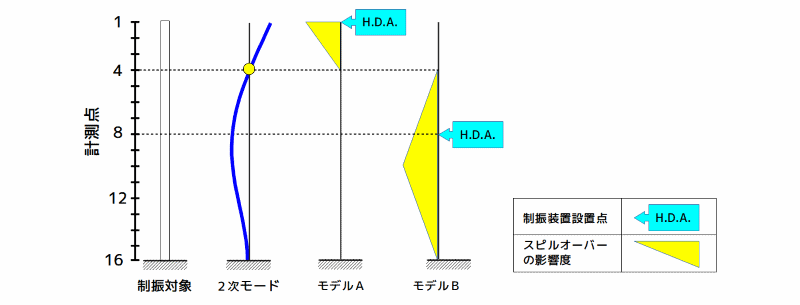
センサー設置位置と制御系の安定性
図 センサー設置位置と制御系の安定性
例えば、塔状構造物先端の点1に制振装置を設置した場合、2次モードの節である点4よりも上方にセンサーを設置すると不安定となり、スピルオーバーを発生します。
また、その不安定度は、センサー設置位置が先端に近づくほど大きくなり、先端部で最大となります。
このことから、同図はスピルオーバー現象を抑制するためには、必ずしも2次モ ードが不可観測となる2次の節にセンサーを設置しなくとも1次モードの制御が可能であることを示しています。
まとめ
「振動モード形を利用したモデリング入門」は、振動モード形の節をセンサー及びアクチュエータ設置点とすることで、スピルオーバーを防止しています。
そこで、センサーを振動モード形の節から移動させた場合の制御系の特性について、1自由度系モデルによる塔状構造物の振動制御を例に実験的考察を行い、2次モードの節を境にセンサーの設置位置により制御系の安定性が変化することを実験的に確認しました。