最初に学ぶ振動と言えば、やはり単振動ということになります。
単振動とは、例えばばねに重りをつけて振動させた時の振動のことです。
ここでは、フックの法則の説明、1個のばねと1個の重りからなる振動系を例に、単振動の変位・速度・加速度の関係と、モデリングの基本である1自由度系のばね・マスモデルについて、できるだけ数式主体ではなく図やグラフを使い説明します。
フックの法則
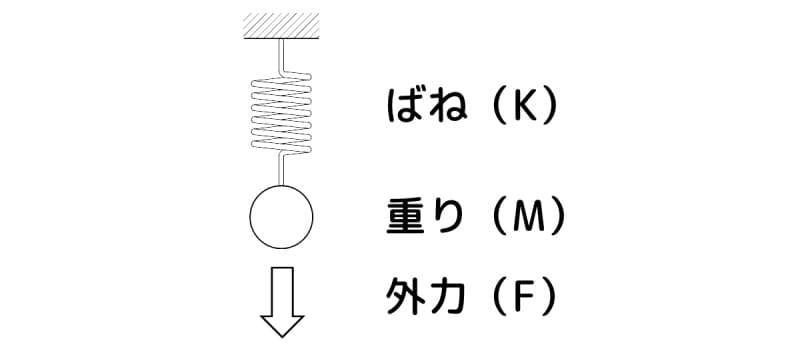
下図において、重りを下方に引っ張るとばねが伸び、重りを上方に押すとばねは縮みます。
この時、引っ張ったり押したりして外力(F)を加えると、手に力を感じます。これを弾性力(復元力)と言います。
ばねと重りと外力
図1 ばねと重りと外力
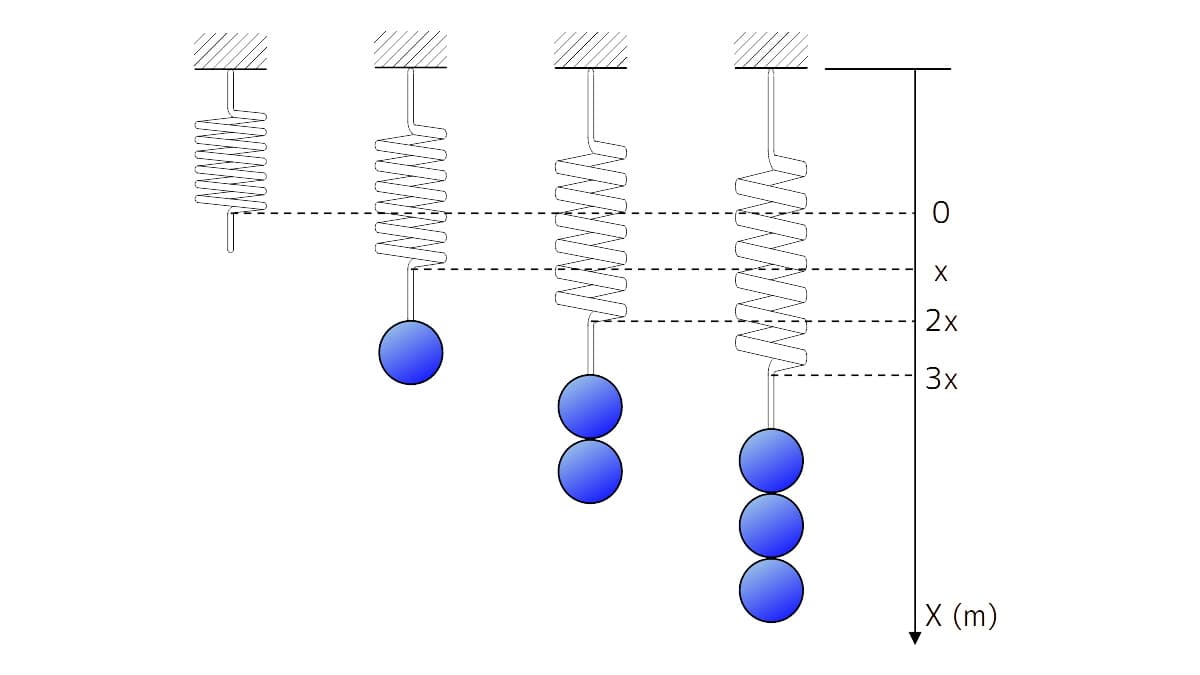
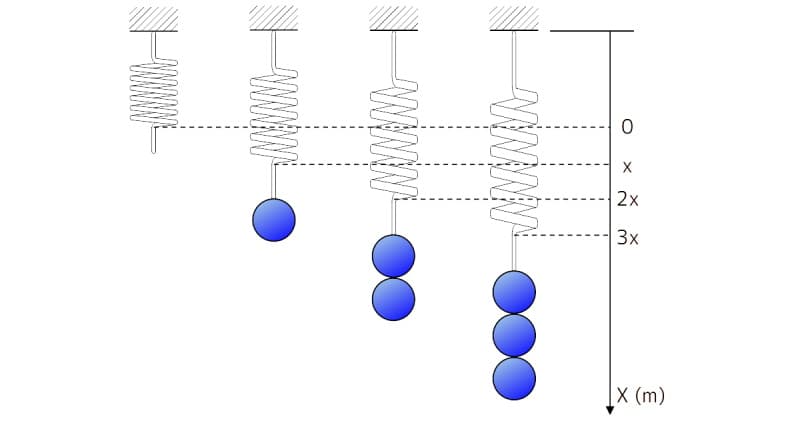
下図は、フックの法則のイメージ図で、次のことを示しています。
- ばねの伸びは、重りに働く重力に比例する。
- 下図で重り1個で伸びが「\(x\)」、2個で「\(2x\)」、3個で「\(3x\)」となる。
- ばねの弾性力(復元力)の大きさは、ばねの伸びに比例する。
- 「\(F = kx\)」から明らか。
フックの法則のイメージ
図2 フックの法則のイメージ
これを式で表すと次式となります。
$$F = kx$$
ただし、
\(F\):弾性力(復元力)(\(N\))
\(k\):ばね定数(\(N/m\))
\(x\):伸びまたは縮み(\(m\))
振動を表す基本的な数式について
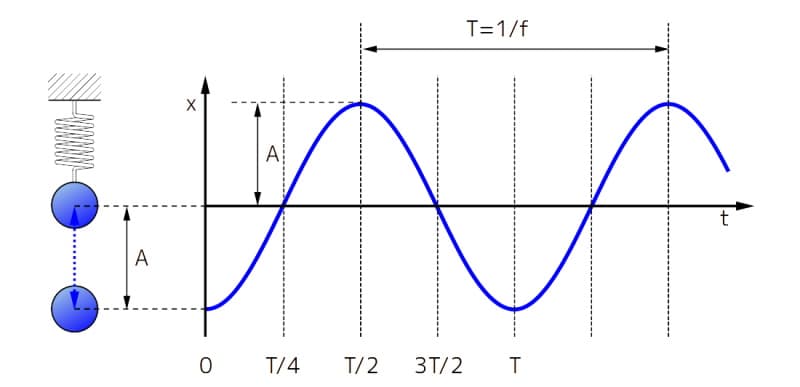
振動を表す基本的な数式について、下図で説明します。
下図において、横軸は時間(\(t\))縦軸は振幅(\(x\))としています。
振動を表す基本的な数式
図3 振動を表す基本的な数式
関連する数式は、
$$T = \frac 1 f$$
ただし、
\(T\):周期(\(s\))
\(f\):振動数(周波数)(\(Hz\))
例えば、1周期が1秒(\(s\))であれば1ヘルツ(\(Hz\))となります。
次に、ばねの上下運動を数式(運動方程式)で表します。
時間(\(t\))における、重りの位置(変位)を\(x\)(\(m\))、速度を\(v\)(\(m/s\))、加速度を\(a\)(\(m/s^2\))とすると、次式となります。
ここでは、簡略化のため初期位相をゼロとしています。
$$x = A cos ( \omega t )$$
速度、加速度は、それぞれ次式となります。
$$v = -A \omega sin ( \omega t )$$
$$a = -A \omega^2 cos ( \omega t ) = – \omega^2 x$$
ただし、
\(A\):振幅(\(m\))
\(\omega\):角振動数(\(rad/s\))
ここで、各振動数(固有振動数)は、次式となります。
$$\omega = \sqrt{\frac k m}$$
\(\omega = 2 \pi f\)、\(T = \frac 1 f\)から、周期(\(s\))は、次式となります。
$$T = \frac {2\pi} \omega = 2\pi\sqrt{\frac m k}$$
ただし、
\(k\):ばね定数(\(N/m\))
\(m\):重りの質量(\(kg\))
以上、数式の説明をしてきました。まとめると次式になります。
$$\omega = 2 \pi f$$
$$\omega = \sqrt{\frac k m}$$
$$T = \frac 1 f$$
振動では、振幅と位相が出てきます。位相は振動の方向、単振動であれば重りの動く向きだと考えると分かりやすいかと思います。
次に、単振動における、重りの位置(変位)、速度、加速度の変化について説明します。
単振動における重りの位置(変位)、速度、加速度
下図を使い、単振動における、重りの位置(変位)、速度、加速度の変化について説明します。
単振動では、重りによる慣性力とばねの復元力とが関係していますが、今の私には説明が難しいので、単振動における重りの位置(変位)、速度、加速度について説明します。
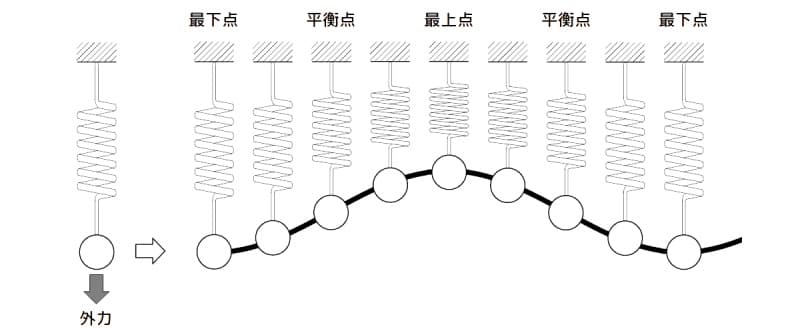
単振動の重りの動き
図4 単振動の重りの動き
重りの変位(\(x\))、速度(\(v\))、加速度(\(a\))のグラフは、下図となります。
$$x = A cos ( \omega t )$$
$$v = -A \omega sin ( \omega t )$$
$$a = -A \omega^2 cos ( \omega t ) = – \omega^2 x$$
なお、簡略化のため初期位相をゼロとしています。下図では、変位(黒の実線)、速度(赤の実線)及び加速度(青の実線)の関係を比較するため、見やすさを優先して上述の式の振幅に相当する値(\(a\)、\(\omega\))を調整しています。
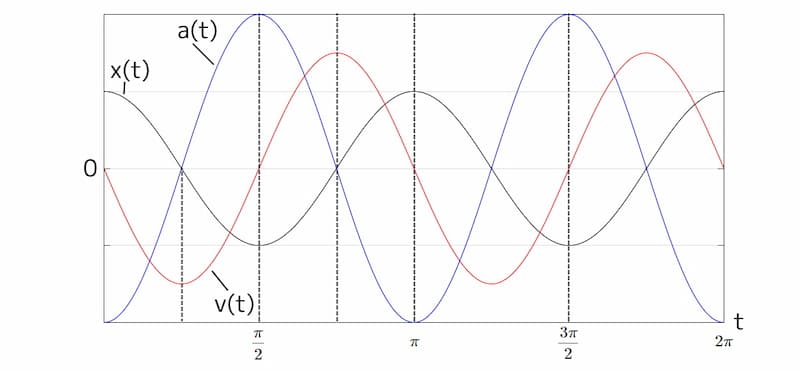
単振動の変位、速度、加速度のイメージ
図5 単振動の変位、速度、加速度のイメージ
上図から以下のことが読み取れます。
- ばねと重りの平衡点では、速度が最大か最小となる。
- 重りの移動方向が、上方から下方、または、下方から上方に切り替わる時、速度はゼロとなる。
- 加速度と変位とは逆方向の波形になる。(振動の形が同じ\(cos\)で正負の符号が逆)
上図のグラフを位相で説明すると、次のように説明されることが多いようです。
- 速度は、変位より位相が\(\pi / 2\)(90º)進んでいる。(上図で右側に\(\pi / 2\)(90º)進んでいる。)
- 加速度は、速度よりさらに\(\pi / 2\)(90º)、変位より\(\pi\)(180º)進んでいる。
一方、現象面から位相に着目すると、次のような説明になります。
- 速度は、加速度より\(\pi / 2\)(90º)遅れている。
- 変位は速度よりさらに\(\pi / 2\)(90º)遅れている。
これは、次の様な考え方、見方によるものです。
- 現象としては、まず加速度が生じ、その結果速度が生じ、その結果変位が生じると考える。
- 速度は、加速度を時間積分している。
- 変位は、速度を時間積分している。

今回、改めてばねの振動について調べてみましたが、意外に奥が深く難しいことに気づきました。1個の質点と1個のばねの運動を数式で表すのは、実は簡単ではなかったと今更ながら考えさせられました。
参考:GNU Octaveのプログラム
## 単振動の変位、速度、加速度のイメージ ## 変位、速度、加速度を見やすく調整 clear; t=0:0.01:2; w=2*pi; ## 変位 y1=cos(w*t); ## 速度 y2=-sin(w*t)*1.5; ## 加速度 y3=-cos(w*t)*2; plot(t,y1,'k', t,y2,'r', t,y3,'b')
1自由度系のばね・マスモデル
これまで、単振動として、質点の変位や力について説明してきました。
ここで言うモデリングは、制御モデルに限らず、FEMなどのシミュレーションツールにも使われています。減衰の扱いについては、実際の物理現象とシミュレーションとの整合については、今でも簡単ではないのですが、シミュレーションをするうえでモデルは必須であり、とても便利なものでもあります。
モデリングの最もシンプルなものが、1個のばねと1個の質量(質点)からなる1自由度系のモデルです。1DOF( 1 Degree Of Freedom)モデルと呼ぶこともあります。
図で表すと下図の様になります。
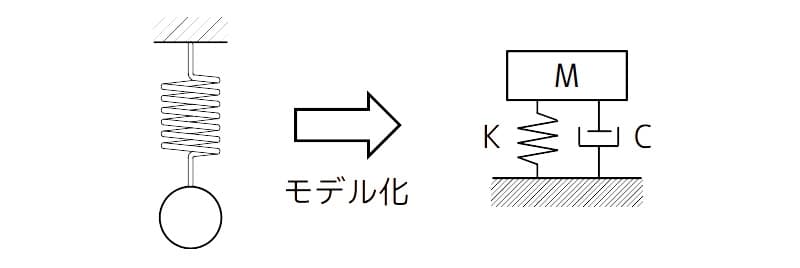
モデリングのイメージ:1自由度系のモデル
図6 モデリングのイメージ:1自由度系のモデル
ただし、
\(M\):質量
\(K\):ばね定数
\(C\):減衰係数
この様に解析対象(ここではばねとスプリング)をモデル化することで、様々なシミュレーションが可能になります。
実験の場合には、条件を1つ変えるにしても準備に手間がかかりますし、条件を変えた場合でも実験の再現性を得るためには知識(ノウハウ)や技術(テクニック)が必要です。
シミュレーションの場合には、例えば質量を変化させた場合の信号を比較するのも簡単に行えます。
実験にもシミュレーションにも前提条件はありますので、それを理解して使っていくことが重要です。


まとめ
最初に学ぶ振動と言えば、やはり単振動です。
ここでは、フックの法則の説明、1個のばねと1個の重りからなる振動系を例に、単振動の変位・速度・加速度の関係と、モデリングの基本である1自由度系のばね・マスモデルについて以下の項目で説明しました。
- フックの法則
- 振動を表す基本的な数式について
- 単振動における重りの位置(変位)、速度、加速度
- 参考:GNU Octaveのプログラム
- 1自由度系のばね・マスモデル