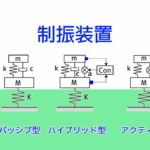
ここでは、振動制御、モデリングに必要なモード解析の基礎知識について以下の項目について説明します。
- モード解析とは
- 振動では、何を問題にするのか?
- モード解析理論
- FEM(固有値解析)と実験モード解析
- 低次元化モデル作成イメージ
ここでは、実験モード解析と有限要素法による固有値解析についてもまとめています。
金属バットを対象にした実験モード解析(ハンマリング試験のデータから簡易的なモード形状の作成)とFreeCADによる固有値解析の例については、以下のページをご参照ください。


モード解析とは
振動の可視化の1つ、振動解析手法の1つで、次の2つに分けることができます。
- 有限要素法の動解析の1つである固有値解析
- 実験モード解析
モード解析は、その結果から、振動モード形(ソフトウェアによってはアニメーション表示もできます)を得ることができ、振動を可視化することができます。
モード解析は、構造上の弱点を見つけ、防振、防音などの対策や設計変更に利用されています。
振動・騒音についての身近な例については、以下の記事を参照してください。
固有振動数と固有モード
ここでは、固有振動数と固有モードについて説明します。
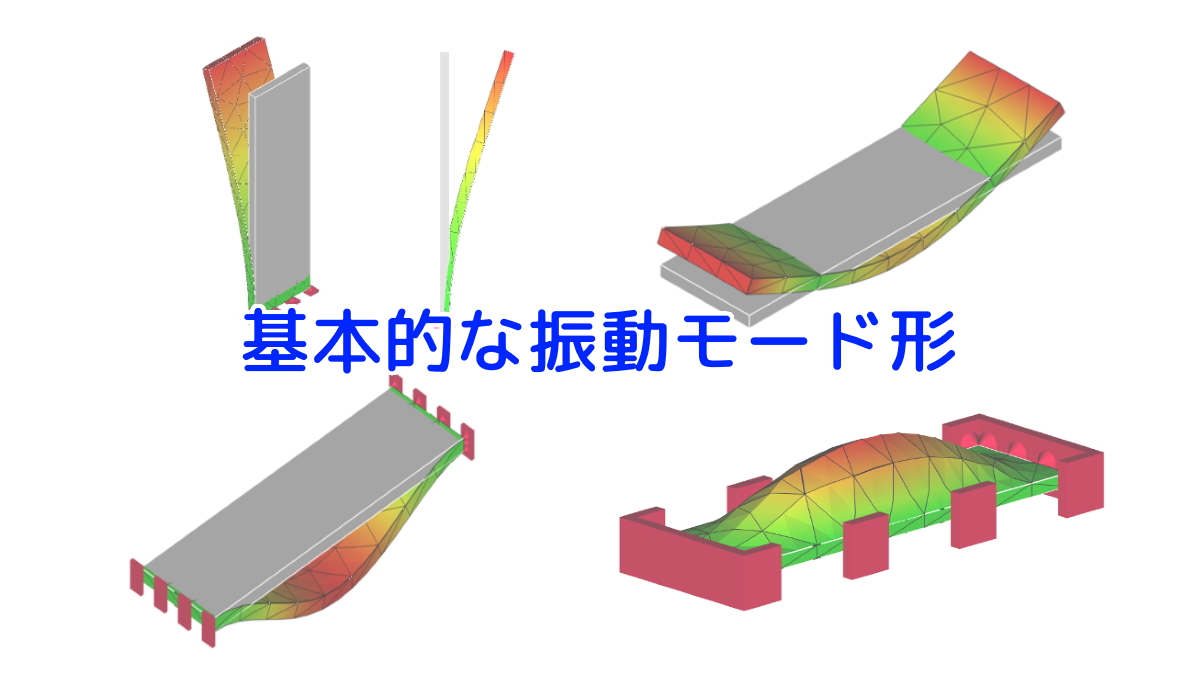
基本的な振動モード形については、以下のリンク先を参照してください。
固有振動数(固有値):振動しやすい周波数
固有振動数(固有値)とは、その対象物固有の振動しやすい周波数であり、周波数応答関数(伝達関数)においてピークとなっている周波数のことです。
下図は、片持ち梁の周波数応答関数の1例です。
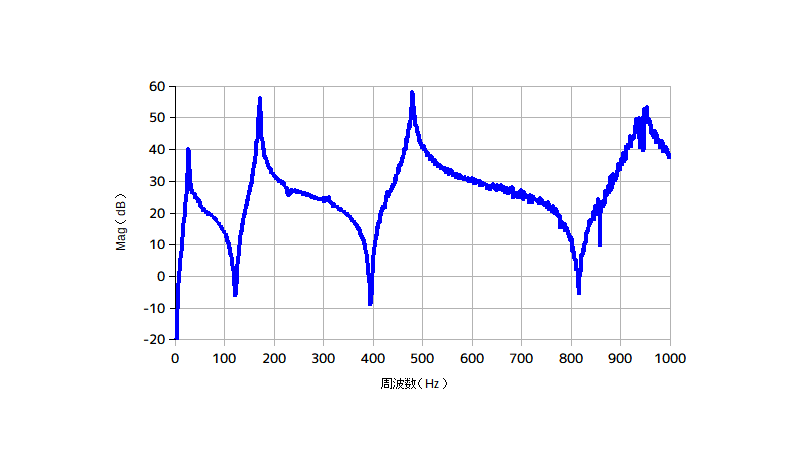
片持ち梁の周波数応答関数の例
この構造物(片持ち梁)では、1000Hzまでに4つのピークがあります。
固有振動数は共振周波数とも呼ばれ、固有振動数近傍で加振すると共振現象となりやすいため、注意が必要です。

実際の製品や構造物は、共振周波数による構造物の振動による破壊を避けるため、様々な対策が行われています。
共振を防ぐためには、
- 機械であれば共振周波数での運転を避ける。
- 構造変更等で剛性を上げる(共振周波数を高い周波数に移動させる。)
といった対策が行われています。
固有モード:固有振動数での振動モード形
一般に構造物は連続体(分布定数系)であり、無限の振動モードを持ちます。
また、ある固有振動数数おける構造物の振動モード形を固有モードといいます。
片持ち梁の1次及び2次の振動モード形を下図に示します。
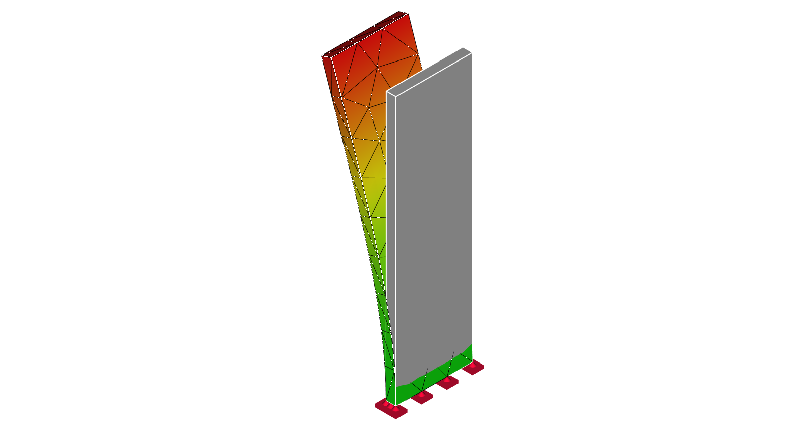
片持ち梁の振動モード形:1次モード
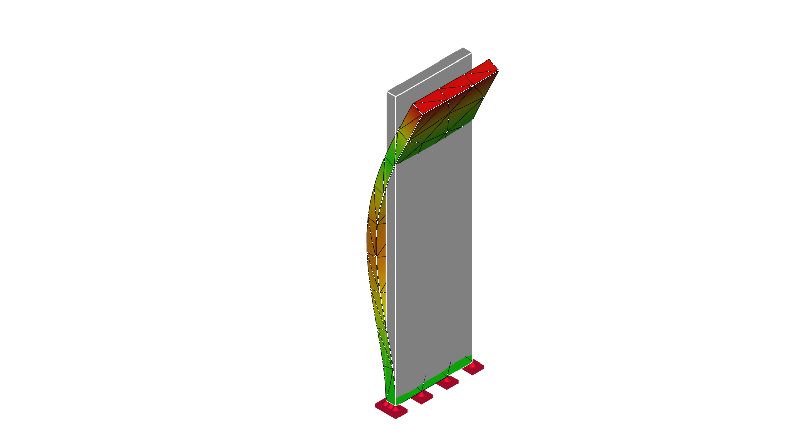
片持ち梁の振動モード形:2次モード
上図の振動モード形において、赤い部分が各モードの振幅が大きい部分を示しています。
ここで、制振するために、振動モード形の節(動かない部分)と腹(大きく動く部分)に注目し、制振装置の設置場所について考えてみます。
- 振動モード形の腹に制振装置を設置すると
- 振動の大きい腹は、良く動く振幅の大きい部分であり、よく動く部分であるためは、振動を止めやすい。
- 上手の振動モード形では、制振対象の先端部(最上部)に制振装置を設置した方がよいことになります。
- 振動モード形の節に制振装置を設置すると
- 振動モード形の節は、振動しない部分であり、制振装置設置位置が節に一致すると、制振することができません。
- センサーを節に設置するとその振動モード形の共振周波数を観測できないため、上図の2次モードの節にセンサーを設置すると制振対象を1自由度系に低次元化したモデルで1次モードの制振効果をえることができます。
振動モード形とモデリングについては、以下の記事をご参照ください。

減衰:どれだけ振動が持続するか?(どれだけ振動がおさまりやすいか?)
減衰とは、外乱等により発生した振動がどれだけ持続するかを表します。
周波数応答関数のグラフでピークとなっている部分が、減衰が大きくなるとピークの鋭さが鈍く(丸く)、ピークの高さは低くなってきます。
つまり、減衰が小さい(ピークが鋭い)ほど、振動は持続し、振動しやすいといえます。
減衰が大きい場合には、制振する場合に共振周波数を含む場合でも、共振現象が大きな問題とはならないため、無理に避けなくても済む場合が出てきます。
減衰そのものは、実験的に求められることが多く、実験モード解析は減衰を求める方法(カーブフィットと呼ばれています)の1つです。
また、減衰の評価は、非常に難しく、誤差が大きいのが現状です。
モード解析理論
モード解析を理論的に説明すると、
- 物理座標系から座標変換により、モード座標系と呼ばれる直交座標系で振動系を解析する手段の1つ
- 数学的は一般固有値分解に基礎を置くもの
となります。
これをイメージにしてみると、下図のようになります。
制振対象(通常は分布定数系)は連成した物理座標系で各モードは連成しているため、分離できません。
モード座標系を導入することにより、1自由度系の足し合わせで表現することができるようになります。
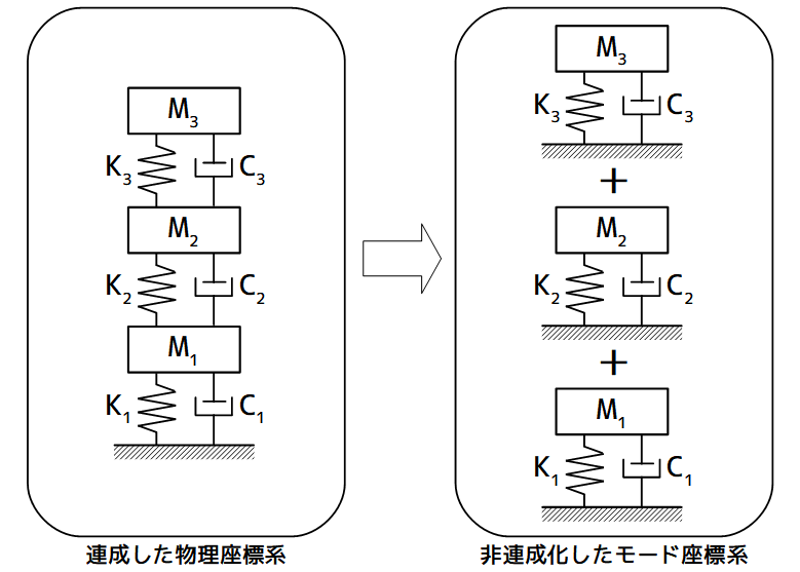
連成した物理座標系から非連成化したモード座標系のイメージ
FEM(固有値解析)と実験モード解析
下図は、実験モード解析とFEM(固有値解析)とのフローについてまとめたものです。左側が実験モード解析、右側が固有値解析です。
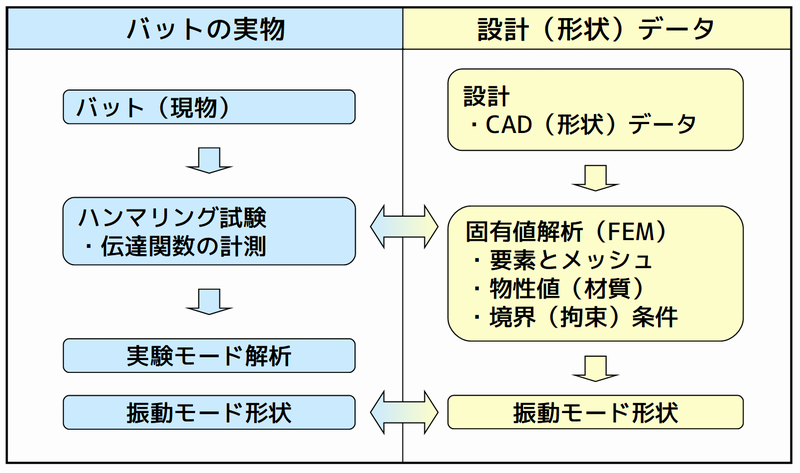
実験モード解析とFEM(固有値解析)の比較
実験モード解析と固有値解析とは、最終的に得るものは振動モード形で同じですが、その求め方は大きく異なることに注意が必要です。
低次元化モデル作成イメージ
実際の制振対象は、分布定数系であり、無限この質量、ばね、減衰からなります。
分布定数系の制振対象の低次元化モデルを作るということは、下図の例では、無限この質点からなる制振対象を2自由度系(2個の質点)へと低次元化しています。
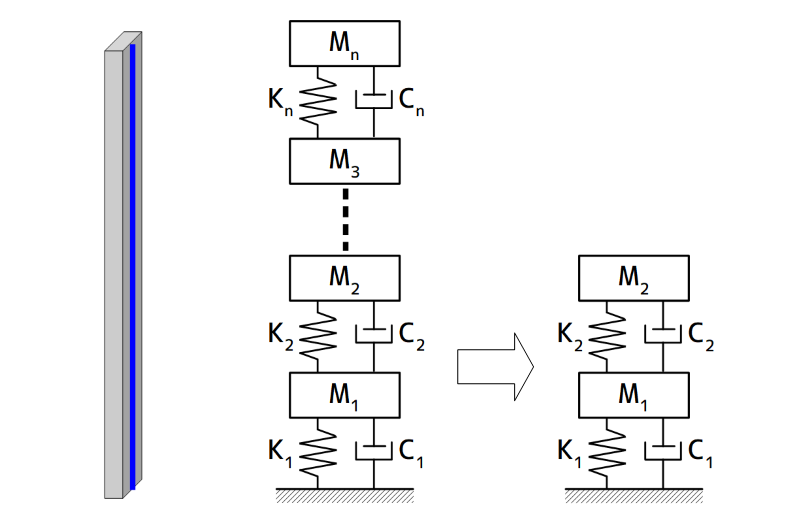
分布定数系から2自由度系の低次元化モデル作成イメージ
まとめ
ここでは、振動制御、モデリングのためのモード解析の基礎知識として、以下の項目について説明しました。
- モード解析とは
- 振動では、何を問題にするのか?
- モード解析理論
- FEM(固有値解析)と実験モード解析
- 低次元化モデル作成イメージ