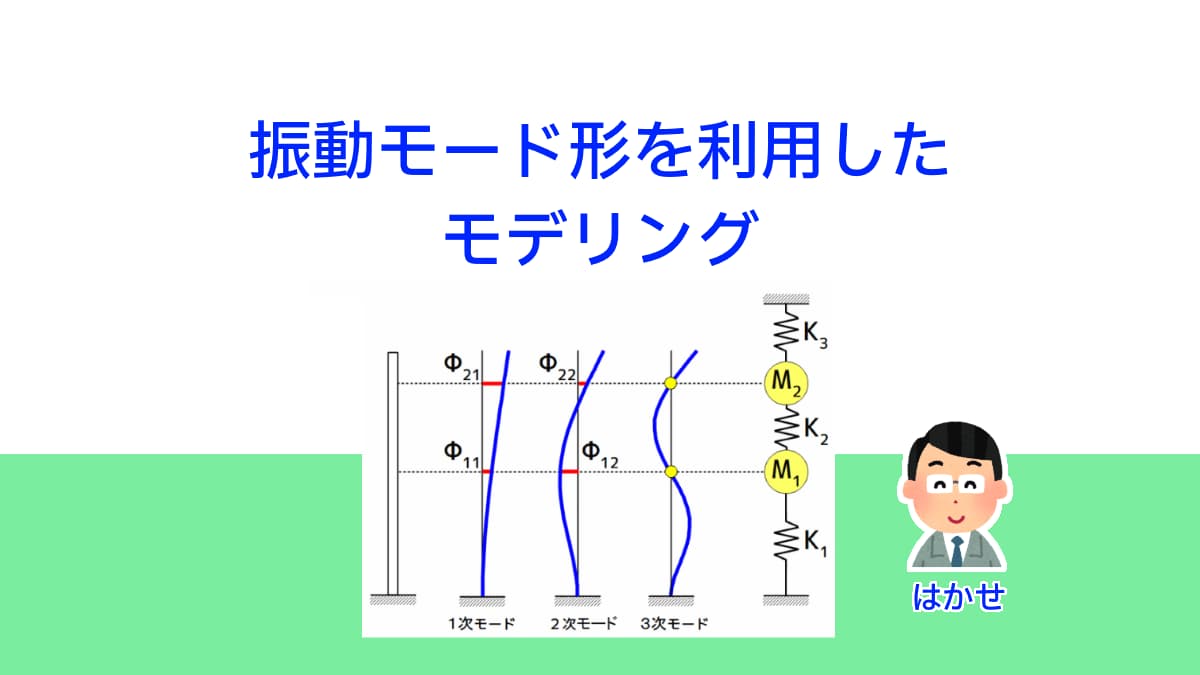
「振動モード形を利用したモデルによるタワー構造物のLQ最適制御入門」では、スカイツリーの様な塔状構造物を対象としたアクティブ振動制御について、モデリング、制御系設計、振動制御実験について説明しました。
ここでは、振動制御を実現するために、次の様な特長があるモデリング方法について説明します。
- 振動モード形を積極的に利用してスピルオーバーを防止
- 物理座標系でのモデリングにより、センサー信号による状態フィードバック制御を実現
パソコンの性能向上と制御系設計ツールの普及
2000年頃からのコンピュータの発達は、振動制御におけるモデリングや制御系設計にも大きな影響を与え、優れた制御系設計ツール(MATLB/SIMULINK等のソフトウェア)が様々な業界に広がりました。
例えば、パソコンで制御系設計ツールを利用して、制御対象を状態方程式で表現し、リカッチ方程式の解を求めLQ制御を実現できるようになりました。
出現当初は、難解で実用性が疑問視されていたLO制御理論を、制御系設計に容易に適用できるようになったのです。
制御系設計ツールは、文字通りの制御系設計だけでなく、モデリングの際にも威力を発揮します。
別の見方をすれば、制御対象をモデリングできれば、制御系を設計し、実際に制御することが容易になったとも言えます。
いくつか具体例を上げておきます。
- 制御系設計ツールが使いやすくなった。
- パソコンのパフォーマンスと操作性向上
- シミュレーションで作成したモデルを実機に組み込む、組み込み系のハードウェアの普及
振動制御の主なプロセス
振動制御の主なプロセスをフローにしてみると下図の様になります。
なお、FEM(固有値解析)については、「FreeCADで始める固有値解析入門:金属バットの振動モード解析」をご参照ください。
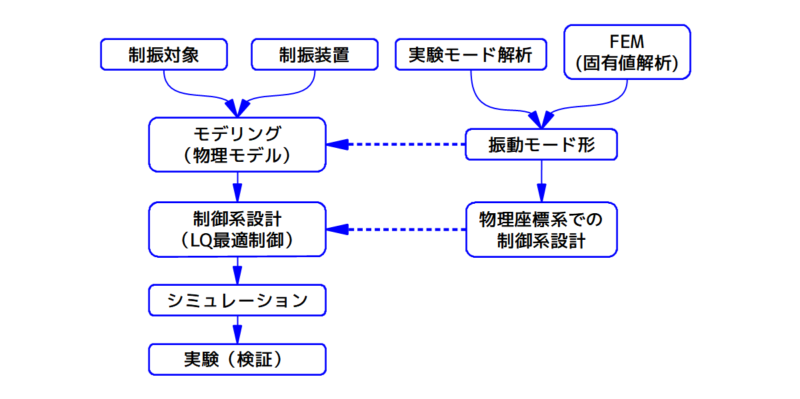
ここで紹介する振動制御のフロー
図1 ここで紹介している振動制御のフロー
塔状構造物を例に、振動制御を実現していくプロセスについて説明します。
制振対象である塔状構造物の形状が決まり、平面内の(水平2方向の)制振をすることになりました。次のようなやりとりがあるのではないでしょうか。
制振対象の塔状構造物の振動について
疑問点は?
- タワーの振動特性(固有振動数と振動モード形状)は?
- どんな風に揺れる?
答えは、
- 基本的には片持ち梁と同じ様な振動モード形になりそうだ。
- 水平2方向では同じ特性となりそうだ。
どのくらい振動を抑える(台風や地震、普段)
制振装置に必要なアクティブ質量の大きさ、質量は、制振装置設置スペース(空間)と共に決まってきます。
タワーや超高層ビルに制振装置を設置する場合、制振効果が大きいのは最上部となりますが、眺望もよいので制振装置設置スペース(空間)は自ずと制約を受けます。
実際の制振装置設置例としては、
- スカイツリーは、ゲイン塔(アンテナ)の最上部に制振装置を2階建てで設置
- 横浜のランドマークタワーは、最上部の4隅のうち対角の2か所に設置
なお、制振装置は1台でも十分な性能を持つそうですが、メンテナンスなども考慮して2台構成となっているようです。
シミュレーションで検証
制振対象も構想図(イメージ図)から、実際の形に、図面になってくるとシミュレーションの出番です。
シミュレーションは、
- 制振対象と制振装置のシミュレーションモデルを作る。
- 制御系を設計する。
- シミュレーションで制振効果を確認しながら、フィードバックゲインを決定する。
といった流れになります。
模型実験でシミュレーション結果の検証
必要に応じ、模型実験(縮尺模型)でシミュレーション結果を検証し、OKとなれば実際の制振装置の製作が始まります。
そして、制振対象(塔状構造物)の建築が進み、制振装置も組み込まれ、まずは制振装置の動作確認(機能確認)をします。
その後、段階的に制振効果を確認し、試行、通常運用、定期的にメンテナンスといったところでしょうか。
現代制御理論によるモデリングの課題と制御系設計
現代制御理論による柔軟構造物の制御系設計においては、柔軟構造物が持つ分布定数系の特性のため、本来無限個である振動モードをモーダルパラメータを用いて低次元化した後、コントローラを設計するのが一般的です。
しかし、制振対象の適切な低次元化モデルが得られなかった場合には、低次元化の際に打ち切った振動モードが、設計したコントローラの制御により励起され、スピルオーバと呼ばれる不安定振動を発生させることがあり、このことが、柔軟構造物の振動制御における重要な課題の1つとなっています。
振動モード形を利用したモデリングと制御系設計のメリット
現代制御理論の1つであるLQ最適制御を実現するための課題、モデリングと重み係数の設定と対策、物理座標系でのモデリングのメリットについて説明します。
モデリングによるスピルオーバーの対策
モデリングの課題とは、LQ制御系を設計するためには、制振対象の低次元化モデルが必要なのですが、この低次元化が適切になされなかった 場合に、スピルオーバの発生が懸念されることです。
このため、塔状構造物の振動制御では、モデリングの際、制振対象の振動モード系の節が持つ不可制御・不可観測性を積極的に活用して、スピルオーバを抑制しています。
重み係数の設定と対策
もう1つの課題である重み係数の設定とは、LQ制御系設計をする上で、希望する制振効果を得るための設計パラメータである重み係数を決定する明確な指針がないことです。
LQ制御系においては、設計パラメータである重み係数行列を設定することで、フィードバックゲインがブラックボックス的に決定されます。
しかし、設計パラメータである重み係数と得られる制御系の制振効果との関係が明らかになっていないため、試行錯誤的に設計パラメータを決定することが多く、一般性に欠ける面があります。
そこで、塔状構造物の振動制御では、制振効果の解析に根軌跡図を活用し、希望する制振効果を得るための重み係数を指定的に決定できる方法を紹介します。なお、これについては、制御系設計(後日、公開します)で説明します。
物理座標系での制御系設計のメリット
物理座標系において制御系設計が可能であれば、低次元化モデルの質量や剛性に物理的意味を持たせ、状態変数とセンサ信号を一致させることができます。
つまり、物理座標系でのモデリングにより、センサー信号による状態フィードバック制御を実現できます。
また、状態観測器(オブザーバー)が不要となるため、センサ信号による状態フィードバック系を構成することができます。
振動モード形を利用した低次元化モデル作成法
「振動モード形を利用した低次元化モデル作成法」とは、振動モード形の節が持つ不可制御・不可観測性を積極的に利用するモデリング手法の1つです。
低次元化のために打ち切った高次モードの不可観測点(振動モードの節)をセンサの設置点に選び、この点とアクチュエータ設置点を質点とする集中定数系物理モデルを作成し、柔軟構造物のスピルオーバを防止するという考え方に基づくモデル作成法です。
柔軟構造物のモード座標系における表現
振動制御とは、外力により構造物固有の振動モードが励起される現象を、制御力を入力することにより抑制することであると言えます。
ここで、励振力を受け減衰を有する多自由度系の運動方程式は、次式のように行列表示できます。
$$\boldsymbol{M} \boldsymbol{\ddot x}\ + \boldsymbol{C} \boldsymbol{\dot x}\ + \boldsymbol{K} \boldsymbol{x} = \boldsymbol{f} \tag{式-1}$$
ただし、
\(\boldsymbol{M}\)、\(\boldsymbol{C}\)、\(\boldsymbol{K}\):質量行列、減衰行列、剛性行列
\(\boldsymbol{x}\)、\(\boldsymbol{f}\):変位ベクトル、力ベクトル
モード解析でN自由度系システムをN個の1自由度系へ
モード解析によれば、N自由度系システムは、N個の1自由度系システムに非連成化することができます。
まず、次式に示す不減衰固有方程式を解いて、固有振動数を要素とする固有振動数行列とこれに対応する固有ベクトルを求めます。
$$\left( – \boldsymbol{\Omega}^2 \boldsymbol{M} + \boldsymbol{K} \right) x = 0\tag{式-2}$$
N自由度系においては、N個の固有ベクトルが存在します。
固有ベクトルを不減衰固有振動数の小さい順に左から並べると、次式の固有モード行列\(\Phi\)となります。
$$\Phi\ = \begin{bmatrix} \phi_1 & \phi_2 & \ldots & \phi_{N-1} & \phi_N \end{bmatrix}\tag{式-3}$$
固有モード行列は、物理座標系とモード座標系との間の変換に用いられますが、一般には、各固有ベクトルは振幅の大きさの絶対値ではなく、各節点での振幅の比で与えられています。
次に、この系が調和振動下にあると仮定して、変位ベクトルと力ベクトルを次式で表します。
$$\boldsymbol{x} = \boldsymbol{x_0} e^{j \omega t}\tag{式-4}$$
$$\boldsymbol{f} = \boldsymbol{f_0} e^{j \omega t}\tag{式-5}$$
ただし、
\(\boldsymbol{x}_0\)、\(\boldsymbol{f}_0\):\(\boldsymbol{x}\)、\(\boldsymbol{f}\) の複素振幅
固有モード行列を用いた物理座標系の変位ベクトルとモード座標系の変位ベクトルとの関係は、次式で表されます。
$$\boldsymbol{x} = \Phi \xi \tag{式-6}$$
(式-1)に、(式-4)、(式-5)、(式-6)を代入し整理すると次式となります。
また、固有モード行列に関する広義の直交性から、(式-7)の\(\boldsymbol{M}\)と\(\boldsymbol{K}\)は、次に示すモード質量行列、及び、モード剛性行列と呼ばれる対角行列になります。
ただし、
\(m_i\)、\(k_i\):i次モードのモード質量、モード剛性
$$\Phi^T \boldsymbol{K} \Phi = \begin{eqnarray} \left[ \begin{array}{ccccc} k_1 & & & & 0 \\ & \ddots & & & \\ & & k_i & & \\ & & & \ddots & \\ 0 & & & & k_N\end{array} \right] \end{eqnarray}\tag{式-9}$$
また、減衰行列が比例減衰(質量行列と剛性行列の線形和)として表される場合には、これもまた次式のように対角化できます。
$$\Phi^T \boldsymbol{C} \Phi = \begin{eqnarray} \left[ \begin{array}{ccccc} c_1 & & & & 0 \\ & \ddots & & & \\ & & c_i & & \\ & & & \ddots & \\ 0 & & & & c_N\end{array} \right] \end{eqnarray}\tag{式-10}$$
ただし、
\(c_i\):i次モードのモード減衰
(式-7)より、i次モードのモード変位\(\xi\)は、次式で表されます。
$$\xi_i = \cfrac{\phi^T_i G_i (\omega)}{m_i \Omega^2_i} f_0\tag{式-11}$$
ここに、\(G_i (\omega)\)は、i次の伝達関数であり、次式で表されます。
$$G_i (\omega) = \cfrac{1}{1 – \left(\frac {\omega}{\Omega} \right)^2 + j 2 \zeta_i\left (\frac {\omega}{\Omega} \right)}\tag{式-12}$$
ただし、\(\Omega_i\)、\(\zeta_i\)は、固有振動数と減衰率で次式で表されます。
$$\Omega_i = \sqrt\frac {k_i}{m_i}\tag{式-13}$$
$$\zeta_i = \frac {c_i}{2 m_i \Omega_i}\tag{式-14}$$
従って、(式-6)は、(式-11)を用いると次式となります。
$$\boldsymbol{x} = \displaystyle \sum_{i=1}^{N} \frac{\phi_i \phi_i^T G_i (\omega)}{m_i \Omega_i^2} f_0\tag{式-15}$$
これにより、a点を励振するときのb点の応答振幅は次式で表されます。
$$\frac{x_b}{f_a} = \displaystyle \sum_{i=1}^{N} \frac{1}{M_{bi}^a \Omega_i^2} G_i (\omega)\tag{式-16}$$
ここで、\(M_{bi}^a\)は、等価質量と呼ばれるものであり、次式で表されます。
$$M_{bi}^a = \frac{m_i}{\phi_{bi} \phi_{ai}}\tag{式-17}$$
これは、(式-15)に示すとおり、N自由度系システムが、N個の1自由度度系システムに非連成化され、物理座標系における応答がN個の1自由度系の応答の線形和として表されることを示しています。
下図は、モード座標系におけるN自由度系構造物のブロック線図表示を示しています。
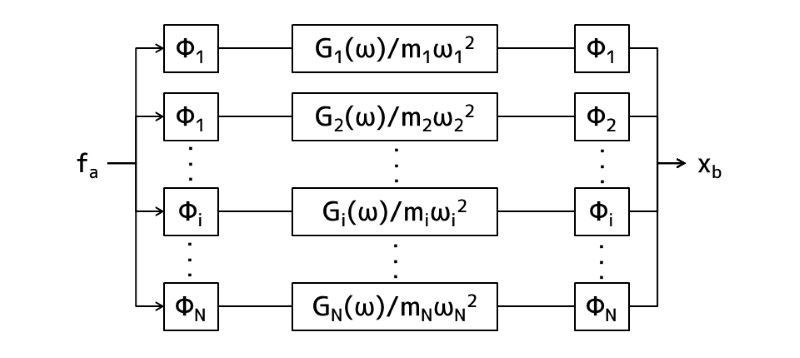
モード座標系におけるN自由度系構造物のブロック線図表示
図2 モード座標系におけるN自由度系構造物のブロック線図表示
振動モード形と不可制御・不可観測性
ここでは、モード解析から導かれた弾性構造物の振動モード形と、現代制御理論で取り扱う可制御性・可観測性の物理的な意味について説明します。
図3は、振動モード形と不可制御・不可観測性との関係を振動モードの節と伝達関数の形で表したものです。
すなわち、ある弾性構造物をモード解析して振動モード形を求め、その構造物の図中点aに制御力を加えたときに、点bで観測された信号をブロック線図で表したものです。
ただし、
\(\phi_{ai}\):i次モードのa点の固有モード成分
\(\phi_{bi}\):i次モードのb点の固有モード成分
\(G_i (\omega)\):i次モードの伝達関数

振動モード形と不可制御・不可観測性(1/2)
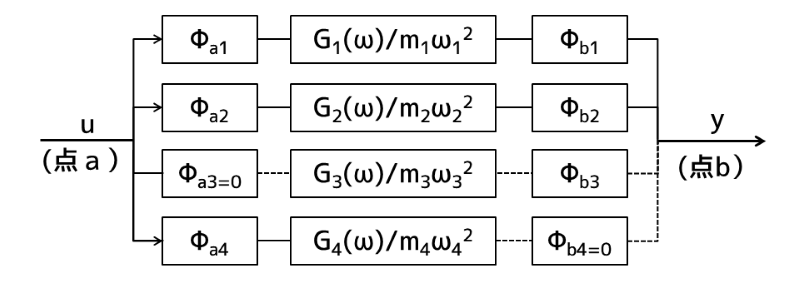
振動モード形と不可制御・不可観測性(2/2)
図3 振動モード形と不可制御・不可観測性
つまり、
- 可制御であるとは、\(\phi_{ai}\)が零でないこと
- 可観測であるとは、\(\phi_{bi}\)も零でないこと
であり、
- これらが零であればそれぞれ不可制御、不可観測
となります。
したがって、振動モード形の節では、不可制御・不可観測を実現できることになります。
振動モード形とスピルオーバー対策
スピルオーバーとは、制御系設計のために低次元化モデルを作成する際に無視した高次モードが、制御系に悪影響を及ぼす現象です。
制御力が無視した高次モードに作用して発生するのが制御スピルオーバ、無視した高次モードを観測することにより発生するのが観測スピルオーバーです。
一般に多自由度系構造物の振動制御においては、スピルオーバーと呼ばれる高次の振動モードによる不安定現象を防止・抑制することが必要になります。
従って、図2の例では、1次と2次モードは可制御・可観測であり制御可能ですが、アクチュエータを3次モードの節に、センサを4次モードの節に配置しているため、本制御系は3次モードに対し不可制御、4次モードに対し不可観測となっています。
このため、制御系設計のために3次及び4次モードを無視して2自由度系の低次元化モデルを作成したとしても、ブロック線図から明らかなように、制御力が出力信号に影響を及ぼさないことになります。
つまり、センサあるいはアクチュエータの設置位置を適切に選択することにより、スピルオーバによる高次モードの不安定振動を抑制することができるということになります。
振動モード形を利用した低次元化モデル作成
これまでの説明内容を振り返りながら、振動モード形を利用したモデル作成法を使い、塔状構造物の2自由度系(2質点系)モデルを作ってみます。
塔状構造物の様な柔軟構造物の振動制御を実現するためには、制振対象の低次元化モデル作成が必須となります。この低次元化が適切でなかった場合には、、低次元化の際無視したモードによるスピルオーバと呼ばれる激しい不安定現象(発振現象)が生じることが懸念されます。
振動モード形を利用した低次元化モデル作成法は、振動モード形の節が持つ不可制御・不可観測性を積極的に利用して、低次元化のために無視したい高次モードの節をセンサーあるいはアクチュエータ(制振装置)の設置場所に選び、その場所を質点とする集中定数系モデルを作成し、スピルオーバーを防止するという考え方に基づいています。
具体的には、振動モード解析より得られた固有モードから、センサあるいはアクチュエータ設置点を質点とする集中定数系の低次元化モデルを作るために、固有モードを修正して必要な質量やばね定数等の物理定数を得ています。
ここでは、物理座標系とモード座標系との関係について説明した後、制振対象である柔軟構造物の固有モードを修正して、集中定数系のモデルを作成する手順をについて説明します。
固有モードの修正による集中定数系モデル作成手順
振動モード形を利用した柔軟構造物の低次元化モデル作成手順は、次のようになります。
- ①制振対象の振動解析
- 制振対象の振動モード解析をする。
- ②制御モデルの次数を決定
- 制御モードと低次元化モデルの次数を決定する。
- ③センサ及びアクチュエータ設置場所の決定
- 制御モード直上(場合によってはより高次のモードも考慮する)の振動モード形の節をセンサあるいはアクチュエータの設置場所に決める。
- ④仮の集中定数系モデルの作成
- モード解析より得た固有モードから、センサあるいはアクチュエータの設置場所を質点とする仮の集中定数系モデルを作成する。
- ⑤固有モードの修正による集中定数系モデルの作成
- 固有モードを修正し、所望の質量,ばね定数等の物理定数を求める。
物理座標系とモード座標系との関係
モード座標系は、固有モード行列中により物理座標系に変換することができます。
ここでは、下図に示す2自由度系モデルを例に、物理座標系とモード座標系との関係について説明します。

物理座標系とモード座標系との対応
図4 物理座標系とモード座標系との対応
ここで、減衰を無視できれば、質量連成の無い2個の質点からなる集中定数系の運動方程式は、物理座標系では次式で表されます。
ただし、
\(M_1\)、\(M_2\):質量
\(K_1\)、\(K_2\):ばね定数
\(x_1\)、\(x_2\):変位
ここで、分布定数系の1次の振動モードから抽出された質点1と質点2の位置における固有モード成分\(\phi_{11}\)、\(\phi_{21}\)、同様に2次の振動モードのそれを\(\phi_{12}\)、\(\phi_{22}\)とすれば、固有モード行列は次式で表されます。
$$\Phi = \begin{bmatrix} \phi_{11} & \phi_{12} \\ \phi_{21} & \phi_{22} \end{bmatrix}$$
物理座標系変位ベクトルとモード座標系変位ベクトルととの関係は、固有モード行列により次式(式-6)で表されます。
$$\boldsymbol{x} = \Phi \xi \tag{式-6}$$
モード座標系の運動方程式は、式-6により次式となります。
ただし、
\(m_1\)、\(m_2\):モード質量
\(k_1\)、\(k_2\):モード剛性
\(\xi_1\)、\(\xi_2\):モード座標系の変位
このように、質量連成のないN個の集中定数系モデルでは、それぞれの質量行列が対角行列となります。
言い換えると質量行列が対角行列であることが、集中定数系が成立するための条件となります。
ところが、分布定数系から集中定数系への低次元化を図る際、
(式-8)のモード質量行列と(式-9)のモード剛性行列を、同時に対角化する固有モード 行列が得られないため、このままでは集中定数系モデルを作ることができません。
そこで、分布定数系の固有モードから任意のモード成分を抽出して、この成分を集中定数系の固有モードとするモード修正法、つまりモデル作成法について説明します。
柔軟構造物の低次元化モデル作成法(質量パラメータによる固有モード修正)
これまで述べてきたモード座標系と物理座標系との関係を活用すると、分布定数系の固有モードを集中定数系の固有モードに修正して、柔軟構造物の任意の点を質点とする低次元化モデルを作成することができます。
ここでは、
質量パラメータを使った固有モード修正による2質点系モデル作成法
について説明します。
なお、質量パラメータに加え剛性パラメータを含めた固有モード修正によるモデリングについては、以下をご参照ください。
質量と剛性パラメータを使った固有モード修正による2質点系モデル作成法
ここでは、仮想ばねを導入することにより、モデルの質量行列を整合(質量行列を対角化)させて、質量集中の条件を満足させる方法について説明します。
下図は、質量パラメータによる2質点系モデル作成法のイメージを示します。

質量パラメータによる2質点系モデル作成法のイメージ
図5 質量パラメータによる2質点系モデル作成法のイメージ
上図において、左から、制振対象の柔軟構造物、制振対象の1次~3次の振動モード形、及び、2個の質点と仮想ばねを含む計3個のばねからなる低次元化モデルです。
まず、仮想ばねを含む物理モデルを仮定し、1次と2次のモーダルパラメータから2自由度系の物理モデルを作成します。
ここでは、モード質量を単位行列にするように正規化した固有モードを正規モードと呼ぶことにします。
正規モードを用いれば、(式-8)の右辺は単位行列となり、物理座標系の質量行列は次のように表されます。
$$\Phi \Phi^T = \boldsymbol{M}^{-1} \tag{式-20}$$
ここで、質点の位置を3次の振動モード形の2つの節とします。(上図参照)
モード解析により1次の振動モード形から求めた3次モードの2つの節における1次の固有モード成分を\(\phi_{11}\)、\(\phi_{21}\)、同様に2次の固有モード成分を\(\phi_{12}\)、\(\phi_{22}\)とすると、仮の固有モード行列は、次のようになります。
$$\Phi = \begin{bmatrix} \phi_{11} & \phi_{12} \\ \phi_{21} & \phi_{22} \end{bmatrix}$$
従って、(式-20)は次式のようになります。
このため、質量集中の条件を満たすためには、次の拘束条件を満たさなければなりません。
$$\phi_{11} \phi_{21} + \phi_{12} \phi_{22} = 0 \tag{式-22} $$
そこで、上式を物理モデルへの変換誤差と考え、次の誤差関数を定めます。
$$\varepsilon_1 = \phi_{11} \phi_{21} + \phi_{12} \phi_{22} \tag{式-23} $$
この誤差関数を零(ゼロ)にするように固有モードを修正します。
そこで、固有モードに対する誤差関数の感度行列を次のように定めます。
$$\begin{bmatrix} \frac{\partial \varepsilon}{\partial \Phi} \end{bmatrix} = \begin{bmatrix} \frac{\partial \varepsilon_1}{\partial \Phi_{11}} & \frac{\partial \varepsilon_1}{\partial \Phi_{21}} & \frac{\partial \varepsilon_1}{\partial \Phi_{12}} & \frac{\partial \varepsilon_1}{\partial \Phi_{22}}\end{bmatrix} \tag{式-24} $$
ここで、\(\Phi_{11}\)、\(\Phi_{21}\)、\(\Phi_{12}\)、\(\Phi_{22}\)について、各々の修正量を\(\delta{\Phi_{11}}\)、\(\delta{\Phi_{21}}\)、\(\delta{\Phi_{12}}\)、\(\delta{\Phi_{22}}\)とします。
誤算関数を零にするような固有モードの修正量を求めるには、次式を解けばよいことになります。
つまり、次式で表される修正量を最小ノルム解を使った一般化逆行列により求め、誤差を零に収束させれば、(式-26)を満足する固有モードを得ることができます。
なお、誤差の収束範囲については、修正後の固有モー ドによるモード形と実際のモード形の形状や節の位置を比較し、ほぼ同一の形状となればよいと考えています。
塔状構造物の2自由度系モデル作成例
下図に示す塔状構造物の低次元化モデル作成例を紹介します。
塔状構造物は、高さ1500mm,、断面が30mm×60mm、厚さ2.3mmの鋼製角パイプ(中空の鋼製角中材)とし、角パイプ下端を垂直にベースプレートに溶接し、これを定盤に固定しています。
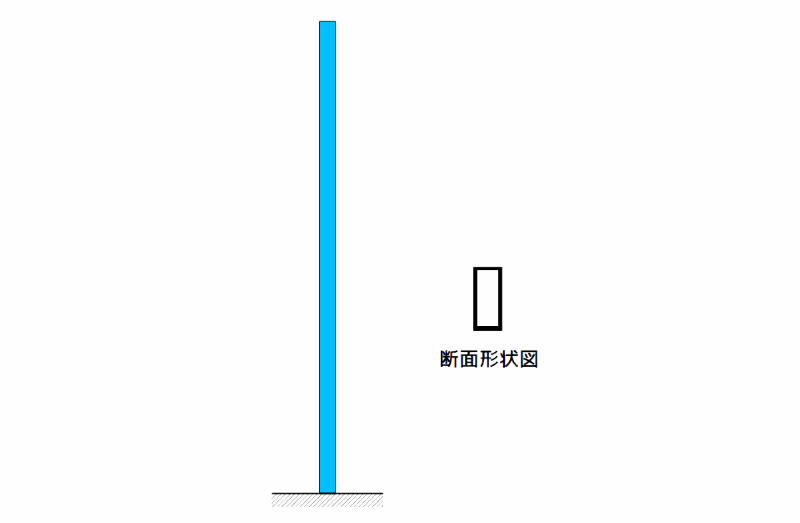
塔状構造物の概要
図6 塔状構造物の概要
まず、実験モード解析により、制振対象である多自由度系構造物の固有振動数と振動モード形を調べます。
塔状構造物と得られた振動モード形と2自由度系モデル(2質点系モデル)は、図5に示す通りです。
ここでは、制御対象モードを、1次と2次の振動モードとし、2自由度系モデルにより制御を行います。
この例では、3次モードによるスピルオーバの発生が懸念されます。そこで、3次モードの2つの節の位置を2自由度系モデルの質点の位置に定め、等価質量同定法により、2自由度系物理モデルを作成します。

等価質量同定法については、以下のリンク先をご参照ください。
等価質量同定法について:モデリング点に質量を付加して等価質量を同定
(式-42)で表される誤差関数を零にするように固有モードを修正した質量行列の一例を以下に示します。
- 固有モード修正前の質量行列
$$\Phi = \begin{bmatrix} 1.42 & -0.67 \\ 0.67 & 3.22 \end{bmatrix}$$
- 固有モード修正後の質量行列
$$\Phi = \begin{bmatrix} 1.35 & 0 \\ 0 & 3.19 \end{bmatrix}$$
ちなみに、これらの物理定数より作成した低次元化物理モデルと分布定数系モデルの周波数応答はほとんど一致しており、この時、(式-42)の誤差関数は零に収束しています。

なお、3自由度系に拡張する場合、誤差関数の数が増えますが、原理的にはここで説明した方法により対応することができます。
まとめ
ここでは、塔状構造物のような柔軟構造物の振動制御法の1つとして、振動モード形の節を利用してスピルオーバーを防止すると共に、物理座標系でのモデリングによりセンサー信号による状態フィードバック制御を実現する低次元化モデル作成法についてまとめました。
モデリングについて以下の項目について説明しました。
- 振動制御の主なプロセス
- 現代制御理論によるモデリングの課題と制御系設計
- 振動モード形を利用したモデリングと制御系設計のメリット
- 振動モード形を利用した低次元化モデル作成法
- 振動モード形を利用した低次元化モデル作成(質量パラメータの修正)
- 柔軟構造物の低次元化モデル作成法
なお、数式については、MathJax-LaTeXを使ってみましたが、WordPressで入力してプレビューで確認を繰り返すのは、学生時代にやったロボットのアセンブラによるプログラミングを思い出しました。