実験とシミュレーションによる振動解析の例として、片持ち梁を例に、実験モード解析とFEMによる固有値解析を行った例を紹介します。
片持ち梁とは、平らな長板(平板)の一端を固定したもので、プールにある飛び込み台のような構造をイメージしています。
解析対象(片持ち梁)について
ここでは、240x60x2 mmのアルミ板を解析対象としています。解析にはFreeCADを使った固有値解析を行っています。
メッシュを切った解析モデルを下図に示します。下図の右端を拘束(固定)しています。

解析モデル
FEMによる固有値解析結果
下表に片持ち梁の1次~10次までの振動モード形の一覧を示します。
| モード次数 | 周波数(Hz) | モード形状 |
|---|---|---|
| 1 | 29 | 曲げ 1次 |
| 2 | 182 | 曲げ 2次 |
| 3 | 233 | ねじり 1次 |
| 4 | 513 | 曲げ 4次 |
| 5 | 724 | ねじり 2次 |
| 6 | 821 | 水平曲げ |
| 7 | 1013 | 曲げ 5次 |
| 8 | 1283 | ねじり 3次 |
| 9 | 1688 | 曲げ6次 |
| 10 | 1942 | ねじり 4次 |
1次~10次までの固有値解析結果より得た振動モード形を以下に示します。
1次モード
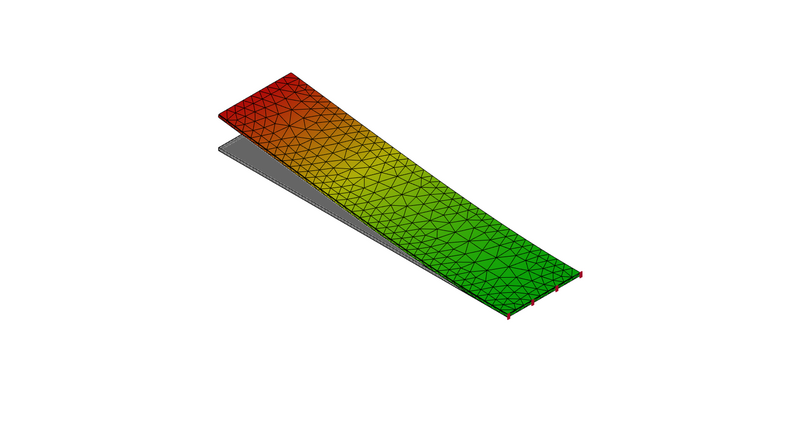
1次モード
2次モード
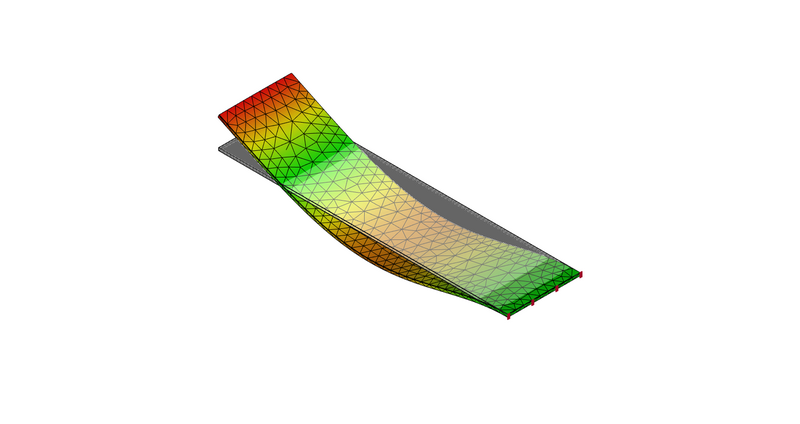
2次モード
3次モード:ねじり
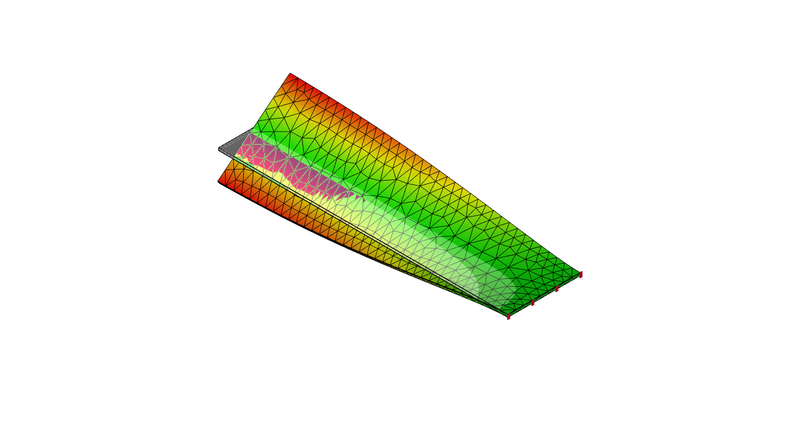
3次モード
4次モード
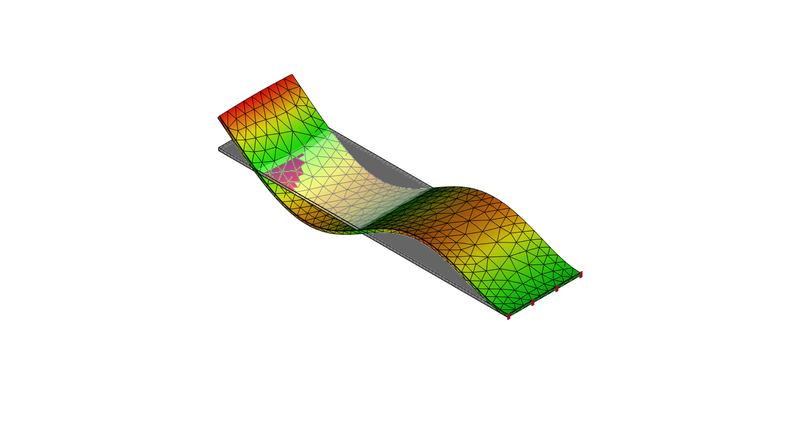
4次モード
5次モード

5次モード
6次モード:水平曲げ
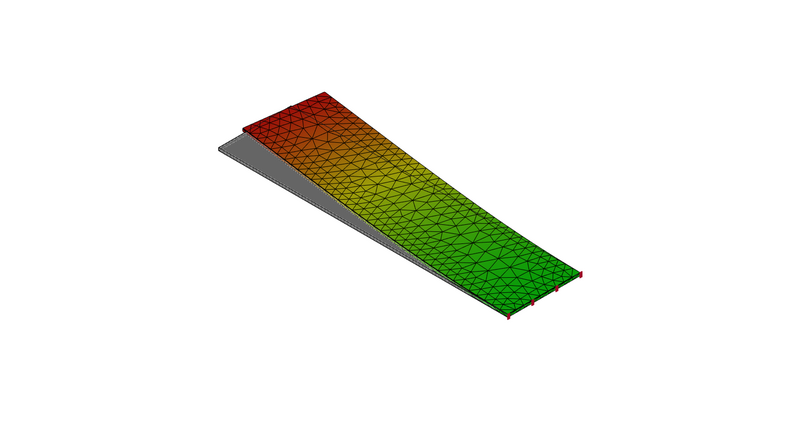
6次モード
7次モード
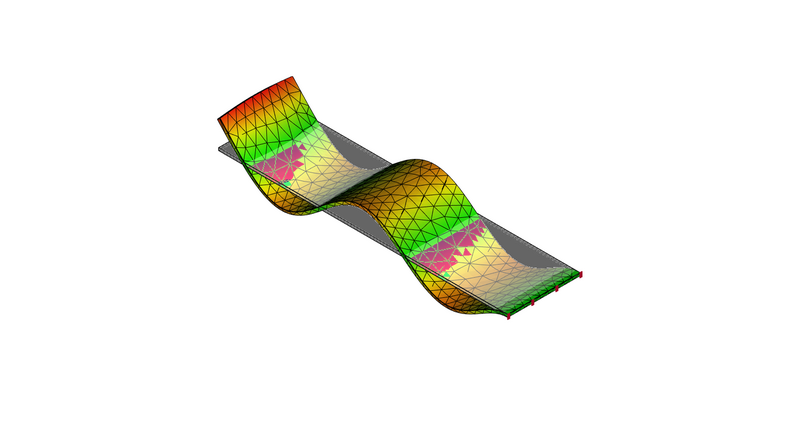
7次モード
8次モード
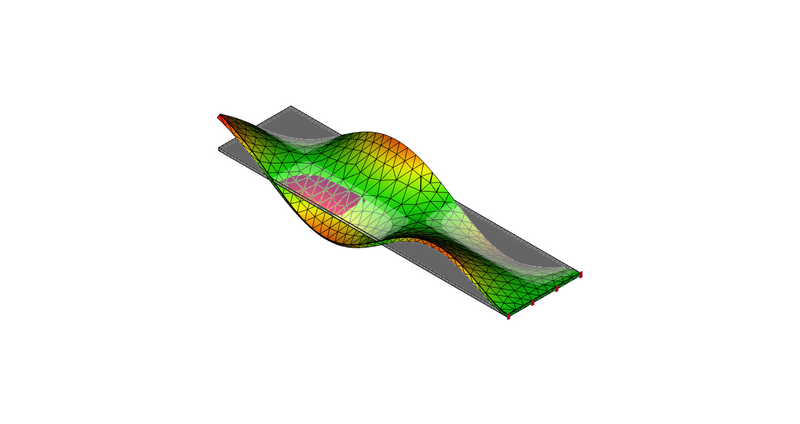
8次モード
9次モード
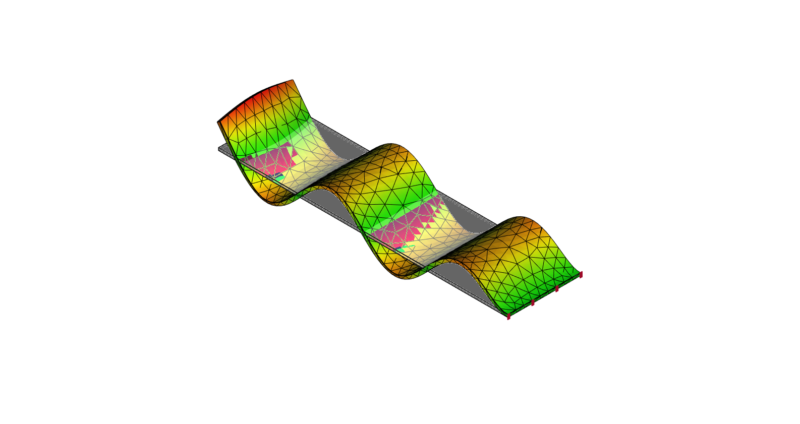
9次モード
10次モード
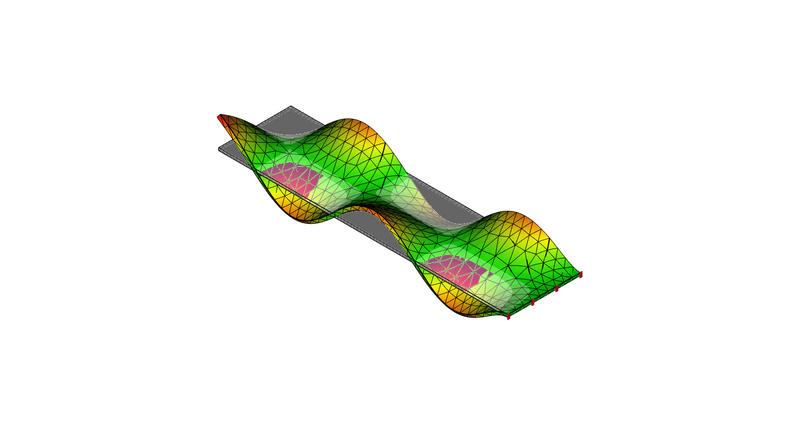
10次モード
実験モード解析結果
ハンマリング試験により周波数応答関数を計測し、固有振動数(共振周波数)での大きさと位相情報(プラスかマイナスか)から簡易的に振動モード形を作成した結果を以下に示します。
【参考】簡易的な振動モード形の作成
下表に作成した1次~3次までの振動モード形の一覧を示します。
| モード次数 | 周波数(Hz) | モード形状 |
|---|---|---|
| 1 | 28 | 曲げ 1次 |
| 2 | 171 | 曲げ 2次 |
| 3 | 480 | 曲げ 3次 |
1次~3次までの振動モード形を以下に示します。
1次モード
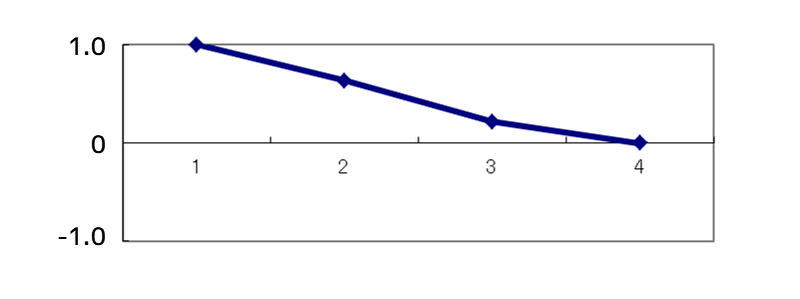
2次モード
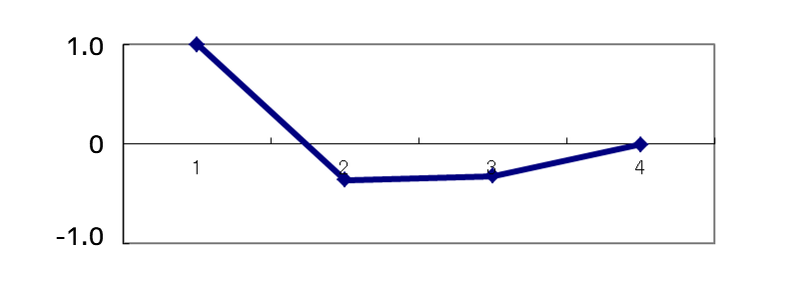
3次モード(FEMでは4次モード)
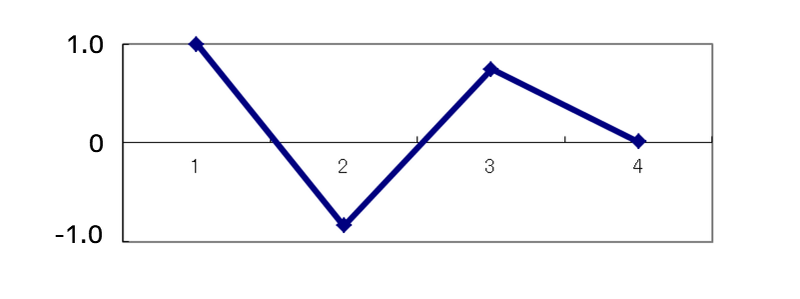
計測点を増やすことで、高次の振動モード形をよりきれいに表すことができます。
なお、高次モードのハンマリングの際には、センサーの変更や計測条件・設定の見直しが必要になることが多いため、低い周波数と高い周波数とに分けて計測することもあります。
実験で得た振動モード形状についての考察
FEMの固有値解析と実験で求めた3個の振動モード形の固有振動数を下表に示します。
| FEM | 実験 | ||
|---|---|---|---|
| 1次 | 29(Hz) | 1次 | 28(Hz) |
| 2次 | 182(Hz) | 2次 | 171(Hz) |
| 3次 | 233(Hz) | - | - |
| 4次 | 513(Hz) | 3次 | 480(Hz) |
実験では、FEMで得られた3次モードが得られていません。
これは、下図に示す計測点1(先端部)の周波数応答関数では、FEMの3次モードの共振周波数(233(Hz))が観測されていないためです。
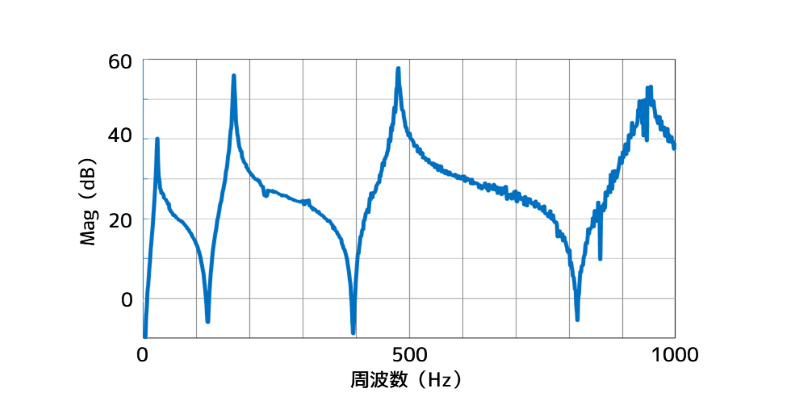
計測点1の周波数応答関数
なぜ「FEMの3次モードの共振周波数(233(Hz))が観測されていない」のでしょうか?
ハンマリング試験では、片持ちはりの長手方向の中央をハンマリングしています。
一方、FEMの3次モードはねじりモードであり、片持ち梁の中心線上は、振動モード形の節になっていることが分かります。
このためFEMの解析結果に含まれる3次モードは、検出(観測)されないため、計測した周波数応答関数に固有振動数が含まれていないことになるからです。
飛び板飛び込みについての一考察
片持ち梁では少々味気ないので、片持ち梁と同じような形状をしているオリンピックの種目の1つである飛び板飛び込みについて考察してみます。

飛び込み台のイメージ
出典:Pixabayからの画像
飛び込む際に飛び板になぜぶつからないか下図を使い考えてみます。
下図の上側の図は、競技者が立つことにより青矢印の飛び板がしなった状態を示しています。
下図の様に飛び板がしなった状態で競技者が飛び板をまっすぐ蹴ると、赤矢印のように飛び板よりも前方方向に飛び出すことになります。
つまり、競技者がまっすぐ、垂直に飛び出したと考えても、実際には前方に飛び出す結果となり、飛び板にぶつかることはないと考えられます。
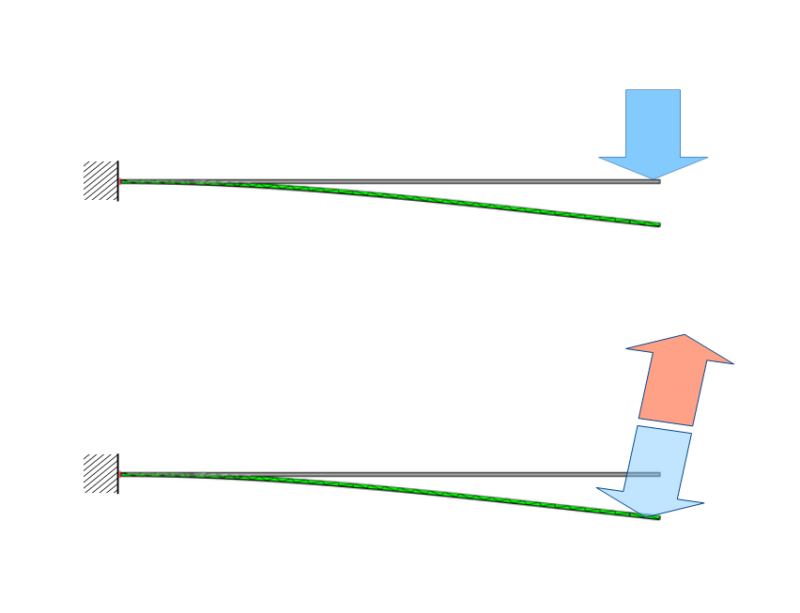
飛び板飛び込みについての考察
まとめ
ここでは、実験とシミュレーションによる振動解析の例として、片持ち梁の実験モード解析とFEMによる固有値解析を行った例を以下の項目で説明しました。
- 解析対象(片持ち梁)について
- FEMによる固有値解析結果
- 実験モード解析結果
- 実験で得た振動モード形状についての考察
- 飛び板飛び込みについての一考察


